In the It-From-Bit series I have reported extensively on Verlinde's 'entropic gravity' concept. I have also provided you with an illustrative 'mikado universe' picture of entropic gravity. This got topped off with my own intuitive notion that in an entropic universe, not only gravity, but also accelerated cosmic expansion emerges. As a result, in one fell swoop, entropy eliminates the need for a fundamental force of gravity as well as the need for dark energy. 

All of this can be summarized succinctly by expanding on an analogy put forward by Dennis Overbye in the New York Times:

There is no elementary force that causes mass to accelerate together and neither is there such a thing as dark energy causing the universe to accelerate. It is just that the big bang made the universe wake up to a bad hair day.

In this fourth It-From-Bit blog post, I will attempt to provide you with an intuitive graphical picture of how entropy effects lead to the emergence of gravitational as well as cosmic acceleration. The first causes matter at short distances to accelerate together, and the second causes matter at large distances to accelerate away. By the time you finish reading this post, you should understand how entropy can be responsible for both these, seemingly opposite, effects.
 

On the origin of bad hair days
If you make a habit of falling asleep with nicely combed hair, and invariably wake up with a hairdo resembling a knotty mess sprouting in all directions, you might be tempted to ascribe this emergence of disorder to a 'hair knotting force' in combination with an 'expansive hair pressure'. This gets even more tempting when, despite vigorous combing, you keep observing hair springing back in a disordered state. Clearly you have to overcome significant randomization forces to restore your hair in a nicely ordered compact configuration. 


Celebrity bad hair day: victim of knotting forces and expansive hair pressure spotted in the wild (1949).

 
When reasoning like this, you have fallen into a conceptual trap. 'Hair randomization forces' do not exist. Just the fact that there is many more ways for your hair to be tangled up rather than being nicely ordered, makes your hair to evolve into a statistically more probable messy state. By tangling up, knotting and expanding disorderly, hair gets more room to express itself.

Are we making the same conceptual error in reaction to the universe's bad hair day?

If so, to avoid this error, we must accept that both gravity and the mysterious cosmic tension referred to as dark energy both cease to exist at a fundamental level. Gravity and dark energy are no more than the large scale consequences of the universe seeking more probable configurations. Mass clogs together and the cosmic expansion speeds up as a result of the universe seeking room to express itself. Some call it a bad hair day, others refer to Murphy's law, while physicists prefer the more quantitative term entropy. No matter what name you attach to it, fact is increasing disorder needs no force to guide it, it's the way things evolve statistically. 


Physical bits: entropy, quanta and degrees of freedom
To understand the entropic origin of gravity and dark energy, we first need to grasp entropy. In essence, entropy is the number of bits required to describe a physical system in all its microscopic details. Rather than speaking about bits, physicists tend to talk in terms of 'the number of degrees of freedom' or the 'number of quanta'. We don't need to be bothered about the differences. For the present purposes we can think of the quanta constituting a physical system as encoding the bits specifying that system.

Physical systems statistically tend to seek configurations that require more bits to describe them. Reason is that a configuration described by, say, 8 bits corresponds to 2⁸ = 256 different microscopic states, while a configuration described by only half of that number of bits would correspond to 2⁴ = 16 microscopically distinguishable states. Physical systems don't have a preference for any of their micro-states, and as a result they do show a tendency towards configurations rich in micro-states, and therefore corresponding to more bits.

This, in a nutshell, is the statistical basis for the second law of thermodynamics: the number of bits or amount of entropy of a system tends to increases due to the microscopic dynamics being impartial to the accessible micro-states. In layman's terms: physical systems seek configurations that allow them more room to express themselves.       

 
Entropic Gravity
Whereas in Newtonian context one can investigate universes consisting of point particles, in general relativity such idealizations do not exist, and we are forced to consider more interesting elementary massive objects: black holes. So let's investigate a model universe consisting of black holes.

In my last post I elaborated on black holes and the holographic principle. The picture that emerges is that for outside observers black holes can be thought of as spherical surfaces capable of accommodating a finite number of quanta. Key result of black hole physics is that the number of quanta is proportional to the surface area. With the mass (or energy) of individual quanta scaling with the inverse of the black hole circumference, the black hole mass (the total mass of all quanta) is proportional to the black hole's circumference.

Combining these black hole results with the above entropy maximization principle, one is tempted to conclude that individual black holes will increase their entropy by growing in size. That would be true, were it not that also black holes have to adhere to the law of conversation of energy. The entropy (or area) of an individual black hole can not grow without increasing its energy (or circumference). 

So how does nature satisfy its hunger for entropy?

That is simple, if one black hole doesn't suffice, add a second. If two black holes of equal mass merge, a black hole will result with a mass equal to the sum of the two.* This means that the resulting black hole circumference will equal the sum of the two initial circumferences, and therefore the resultant entropy (or surface area, which scales with the square of the circumference) will double.



Two equally sized black holes merging together (cross-sectional view). The net effect is that the total circumference doesn't change, while the total area (entropy) doubles.            

From the second law of thermodynamics, it follows that black holes will tend to move together and merge, thereby forming a configuration richer in entropy. We have given this effect the name 'gravity', and for many years assumed it to be associated with a fundamental force. It is not, it is a statistical (entropic) effect.

Studying in more detail two black holes approaching each other, it becomes evident that both will undergo surface area (or entropy) increases, even when their mutual distance is much larger than their individual diameters. When doing the math, it follows that for large distances these entropy increases correspond to an entropic acceleration given by Newton's one-over-distance-squared law. This is what is at the heart of Verlinde's observation that gravity is an entropic effect.     


Entropic cosmic acceleration 
Ok, so black hole mergers lead to entropy increases. Is there another way for our black hole universe to increase entropy? You might be surprised to hear that there indeed is an alternative way for total surface area (and thereby entropy) to increase. In fact, it is a much more straightforward way: the total surface area of a system of black holes will increase when additional black holes enter the system. 

How could that happen in our model universe? Well, we have to be a bit more precise here: often when we are talking about 'the universe' what we really mean is the observable universe. This observable universe is bounded by a cosmic horizon. The term horizon is very appropriate here, but denotes a more fundamental limitation than we are used to. The cosmic horizon indicates the cosmic depth beyond which observation is physically impossible. It is the distance at which the cosmological redshift becomes unbounded, and time seems to get to a stand-still. For an expanding universe, the cosmic horizon and distant objects all recede. Objects will enter the observable universe causing its entropy to increase, provided the cosmic horizon recedes faster and overtakes the most distant objects. This mechanism is illustrated in below animation.            


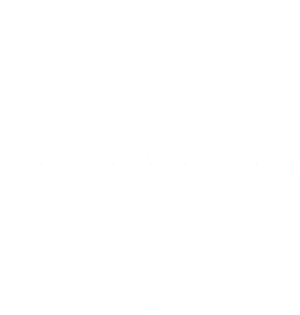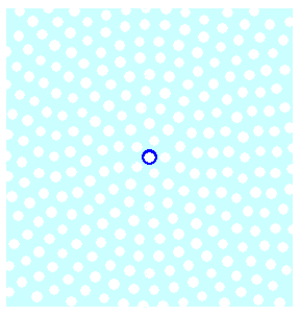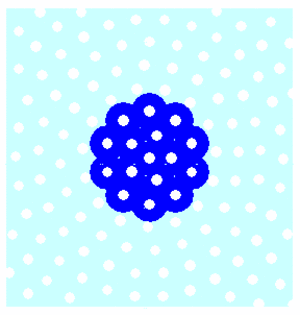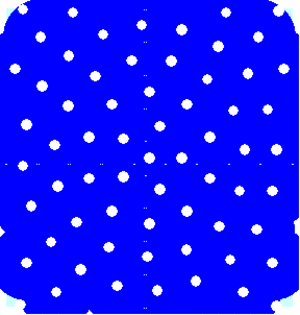
Entropic cosmic acceleration at work in the black hole universe (cross-sectional view). While the black holes (white circular holes) move away from each other, the cosmic horizon (the edge of the observable universe indicated in dark blue) overtakes the receding black holes. Although no black holes merge, the entropy of the observable universe (total surface area of the black holes contained within in the observable universe) obviously increases.

It should be clear that nature's hunger for high entropy configurations will lead to a combination of affects shown in the two animations above. Entropy increases by black holes merging, as well as by the observable universe expanding. When doing the math, both effects result in accelerations: massive bodies accelerate toward each other, and the observable universe undergoes an accelerated expansion. The key conclusion to be drawn from all this is that these effects do not require a fundamental force of gravity, and neither do they follow from a mysterious dark energy dominating the universe, yet unobservable other than by it's effect on the cosmic expansion. Both acceleration effects are the direct result of what one should expect to happen statistically without a fundamental force of gravity or dark energy to be present.


Word of warning
To conclude, a word of warning: although since my original entropic universe post several research groups have embraced the entropic universe concept described above, not all it's consequences have been derived yet. In particular, the entropic expansion of the universe differs from the expansion described by the standard model of cosmology, the lambda-CDM model. Further investigations are required to compare the behavior resulting from the entropic expansion model to the same data used to fit the parameters in the lambda-CDM model. 

No matter how appealing these ideas might seems, if they don't fit the data we need to scrap them. Watch this space.   


---------------------------
* This would be true if one could execute a controlled merger. In reality, black hole mergers are uncontrolled explosive events that will cause some of the mass to be ejected. As long as less than about 29% of the total mass gets ejected, there will still be an entropy increase albeit not an entropy doubling.