Various situations involving social interaction drag you into a negative sum game, and make you part of a misbehaving gang. Welcome to Braess' paradox.
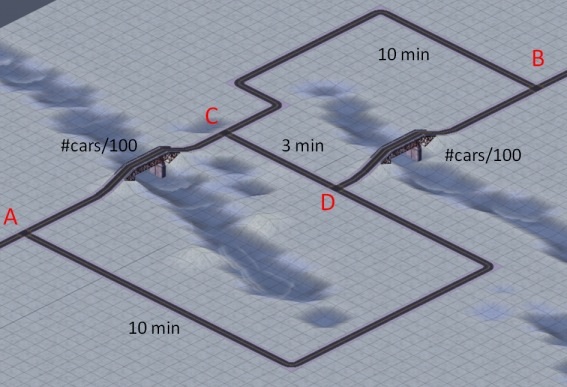
Each morning at rush hour a total of 600 commuters drive their cars from point A to point B. All drivers are rational individuals eager to minimize their own travel time. The road sections AD, CB and CD are so capacious that the travel time on them is independent of the number of cars. The sections AD, and CB always take 10 minutes, and the short stretch CD takes no more than 3 minutes. The bridges, however, cause real bottlenecks, and the time it taken to traverse AC or DB varies in proportion to the number of cars taking that route. If N is the number of cars passing a bridge at rush hour, then the time to cross the section with this bridge is N/100 minutes.
Given all these figures, each morning each individual driver decides which route to take from A to B. Despite the freedom of choice for each commuter and despite all traffic flow information being available to each and every commuter, the outcome of all individual deliberations creates a repetitive treadmill. Each morning all 600 commuters crowd the route ACDB and patiently await the traffic jam at both bridges to resolve. The net result is a total travel time of 600/100 + 3 + 600/100 = 15 minutes for each of them.
Does this make sense?
At this stage you may want to pause and consider the route options. If you would be one of the 600 commuters, would you join the 599 others in following route ACDB?
Of course you would. There is no faster route. Alternative routes like ACB or ADB would take you 600/100 + 10 = 16 minutes, a full minute longer than the preferred route ACDB. So each morning you and 599 other commuters travel along route ACDB and patiently queue up at both bridges.
One day it is announced that the next morning the road stretch CD will be closed for maintenance work. This announcement is the talk of the day. Everyone agrees that this planned closure will create havoc. Would section AD or CB be closed, it would have no impact as these are idle roads. But section CD is used by each and every commuter. What a poorly planned maintenance, a closure of such a busy section should never be scheduled for rush hour!
The next morning all 600 commuters enter their cars expecting the worst. Each of them selects between the equivalent routes ACB and ADB. The result is that the 600 cars split roughly 50:50 over both routes, and that both bridges carry some 300 cars. Much to everyone's surprise all cars reach point B in no more than 300/100 + 10 = 13 minutes. Two minutes faster than the route ACDB preferred by all drivers.
How can this be? If a group of rational individuals each optimize their own results, how can they all be better off when their individual choices are being restricted? How can it be that people knowingly make choices that can be predicted to lead to outcomes that are bad for everyone?
Asking these questions is admitting to the wishful thinking that competitive optimization should lead to an optimum outcome. Such is not the case, when multiple individuals compete for an optimal outcome, the overal result is an equilibrium and not to an optimum. We saw this in the game Prisoner's Dilemma, and we see it here in a situation referred to as Braess' paradox.
A question to test your understanding of the situation: what do you think will happen the next day when section CD is open again? Would all players avoid the section CD and stick to the 50:50 split over routes ACB and ADB, a choice better for all of them?
If all others would do that, that would be great news for you. It would give you the opportunity to follow route ACDB and arrive at B in a record time of about 9 minutes (300/100 + 3 + 301/100 minutes to be precise). But of course all other commuters will reason the same. So you will find yourself with 599 others again spending 15 minutes on the route ACDB. And even with the benefit of hindsight none of you will regret the choice you made: any other route would have taken you longer. Yet all of you surely hope that damn shortcut between C and D to get closed again.
And don't assume this phenomenon doesn't occur in real life.
--- This article also appeared at HammockPhysicist.wordpress.com ---




Comments