Two and a half months since Erik Verlinde submitted his entropic gravity paper, and all of physics and cosmology has turned into entropy. Well, I am exaggerating a bit, and perhaps more than just a bit. Yet, fact is that within two weeks of Erik's publication a steady stream of 'entropic everything' papers has developed at a rate of close to one paper per day. Gravity, Einstein's equations, cosmic expansion, dark energy, primordial inflation, dark mass: it's all entropic. Chaos rules. Entropy is king!
Or is it?
Could it be that an 'entropic bandwagon' has started rolling? Is this all not just a fad appealing to scientist tired of string theory? What is this elusive entropic force anyway? Do these folks really believe bits of information attract each other?
Of cause not. Bits don't attract, and entropy doesn't pull. The term 'entropic force' seems to wrong-foot large groups of readers (and some physics bloggers alike). Entropic interactions are not mediated by forces acting at micro scales. Entropic forces exist even in systems that at a microscopic level poses no energies other than kinetic energy. Yet, at a macroscopic level such systems are subject to configurational accelerations. These accelerations result simply from certain configurations corresponding to a larger number of micro states than others. This, combined with the tendency of physical systems to sample the microscopic states in an unbiased way, yields a macroscopic dynamics that prefers configurations that are denser in terms of micro-states.
Puzzled? Let's look at some simple, yet progressively more realistic examples.
Tetrahedron Hole Dynamics
We start with a seemingly trivial toy model. A model that strips entropic attraction to its barest essentials. You might feel this Mickey Mouse model can impossibly have any bearing on the problem of entropic gravity.
Be patient, I promise you all will become clear in a minute!
Our toy universe consists of six 'ray paths' that form the edges of a tetrahedron. Each ray path can be in two distinct states: occupied or empty. This accounts for a total of 26 = 64 states. Three ray paths meet at each vertex. If all three are empty, the vertex represents 'a hole' that gets filled with at least one particle. If any of the three ray paths is occupied, the vertex is 'full' and can not contain any particle.
We investigate configurations with two particles, and therefore limit the tetrahedron configurations to those containing one or two holes. The dynamics is straightforward. We label the ray paths '1'..'6', construct a suitable starting configuration, and grab a die.
Throw the die, note down the number of spots, and check the corresponding ray path in the tetrahedron:
A) If the ray path is occupied, make it empty, unless doing so would create more than two vertices containing particles.
B) If the ray path is empty, occupy it, unless this would result in zero particle vertices.
Again throw the die and repeat ad infinitum.
This simple process creates a sequence of configurations, each of which contains two particles occupying either two different vertices (two particles in two distinct holes), or the same vertex (two particles in the same hole). Below animation clarifies the process.
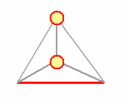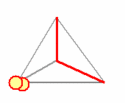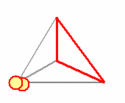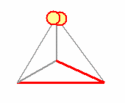
The tetrahedron 'universe'. The edges change from 'empty' (grey), into 'occupied' (red) such that there are always one or two 'holes': vertices where three empty edges meet. This edge dynamics dictates the movements of two particles that hop from vertex to vertex such that any hole contains at least one particle.
In this model there is no explicit force acting between the two particles. So one might naively postulate that both particles will jump randomly from vertex to vertex, and will be as often at the same vertex as at different vertices. This is not the case. The reason is simply that there are 16 states with one hole, against only 6 states with two holes (by allowing only for one and two-hole configurations, 42 of the 64 total number of microstates are forbidden).
Another way of looking at this is that for a given vertex to contain a particle, the three ray paths meeting at that vertex need to be empty. This reduces the entropy (the number of bits needed to describe the tetrahedron universe) by three. For two given vertices to contain a particle, both vertices need to have three empty ray paths. One would therefore expect an entropy reduction of 3 + 3 = 6 bits. However, both vertices necessarily have one ray path in common, and an entropy reduction of 6 – 1 = 5 bits results. However, if both particles are accomodated at the same vertex, both particles dictate the same three ray paths to be empty. In other words: there is 3 common ray paths and an entropy reduction of 6 – 3 = 3 bits results. So, the two particles being together at the same vertex creates a smaller entropy reduction compared to the case of the two particles being seperate. In other words, two particles together at one vertex corresponds to significantly more states than two particles at separate vertices. This is all that is needed for a tendency for both particles to stick together.
The Mikado Universe
Now we are ready for the next step. The mikado universe. Still a toy model, but I promise you we are getting closer to 'the real thing'.
Imagine a two-dimensional space spanned by a large number of ray paths. Think of each ray path as extending indefinitely, and the whole network of ray paths forming a discrete Planck-scale configuration from which the planar space emerges. Like in the tetrahedron universe, each ray path represents an elementary degree of freedom of the system: it can be occupied or empty. We will interpret a ray path being occupied, as a causal influence being transmitted via the ray path. (More about that later.)
We need particles in our model, and therefore restrict the allowable mikado universe configurations to those containing enough empty ray paths such that we have available two 'holes'. In this model holes are defined as regions not crossed by any occupied ray paths, and large enough to contain a circle of given radius. Below figure clarifies the concept.
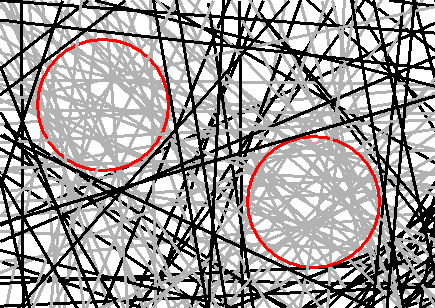
The mikado universe. The straight lines represent the ray paths. The ray paths shown in gray are 'empty' and do not contribute to the entropy. As a result two 'holes' exist: regions void of causal influences large enough to contain circles of specified radius (indicated in red).
Now imagine a dynamics similar to that in the previous example. We label the ray paths '1', '2' ... 'N', construct a starting configuration with two holes, and grab an N-sided die.
Throw the die, note down the number of spots, and check the corresponding ray path in your mikado universe:
A) If the ray path is occupied, make it empty.
B) If the ray path is empty, occupy it, unless this would cause one or both of the holes no longer capable of fitting the circle of given size.
Again throw the die and repeat ad infinitum.
What will you see happening would you be patient enough to go through many of these steps? If you have understood the tetrahedron model, the answer is simple. You will see both holes moving towards each other.
Why is that?
Like in the tetrahedron model, there are more micro-configurations available when the holes are closer together. To see why this is the case, first consider two holes far apart. Each hole requires a certain number of ray paths to be empty. Each hole thereby reduces the overall entropy by a corresponding number.
Now place the holes close together. Again, each hole rules out a certain number of ray paths from becoming occupied. However, as both holes are in each other's vicinity, the set of ray paths prevented by hole 1 from becoming occupied will have an overlap with the set of ray paths prevented by hole 2 from getting occupied. Like in the tetrahedron model, the two holes being closer together creates a smaller entropy reduction compared to the case of the two holes being far apart. And the result, as we know by now, is an entropic attraction.
Now, for this model we can even deduce how the entropy drop reduces when the holes move together. And knowing this entropy drop, we can derive the distance dependency of the entropic force.
All we have to calculate is the scaling of the number of ray paths crossing both holes. For a uniform and isotropic distribution of ray paths, this number S is proportional to the radii (r1 and r2) of both holes and inversely proportional to the distance (R) between both hole centers:
S ~ r1 r2 / R
The entropic force is proportional to the gradient of this number:
F ~ dS/dR = -r1 r2 / R2
Here, the minus sign indicates the force to be attractive.
Finally, we ask ourselves what really are these holes of given radius? You might have noticed that no occupied ray paths leave these holes. With occupied ray paths interpreted as paths along which causal influences propagate, this means that no causal influence leave these holes. Sounds familiar, right? Indeed, the holes in the mikado model can be thought of as black holes. And black holes have a radius r proportional to their mass M. So, we finally have:
F ~ - M1 M2 / R2
OK, let's call in Sir Isaac...
The Real Thing
Are you ready for the real model of the universe?
...
Well, maybe you are ready, but I am afraid I have to disappoint you. I have no 'real' model. No one has.
“What about the above mikado universe?” you might ask. “That did lead to the right equation for Newtonian gravity, right?” Well, yes. But I did cheat by more than a bit. Firstly, I presented a two-dimensional universe. Would I have constructed the same mikado model in three-dimensions, things would not have worked out so nicely. In order to make things work in three dimensions, the number of ray paths need to be diluted with distance in such a way that a two-dimension behavior results. In other words, a holographic description needs to be introduced. (You are not surprised by that, are you?)
Secondly, for a model like this to make physical sense, it needs to be properly embedded not in space, but in spacetime. So we even need to go one dimension higher (and retain the holographic description).
Thirdly, the fixed ray path network violates various physical symmetries. And also the model is not quantum mechanical in nature. And there are several more problems with this model, some more subtle than others.
But we need not go into all of these. In physics it is entirely valid to construct models with shortcomings, provided these models do provide certain insights. And such is the case here. We have seen how a force-free and almost trivial microscopic dynamics can lead to an attractive force at macroscopic scales. But there is more. The model also elucidate other important aspects of entropic gravity.
One such aspect has to do with the question of the reversibility of entropic gravity forces. Some have claimed that entropic forces are necessarily irreversible. In other words, in a system with entropic gravity it would in general not be possible to cause the system to trace back its history.
Reversible Entropic Forces
The claim that entropic forces are necessarily irreversible is a misconception. Verlinde has tried to argue against this wrong concept, but he failed to note a key point. Key is that if the underlying microscopic (Planck scale) dynamics is reversibility, so will be the emerging entropic force.
Using the above models, it should be immediately clear that entropic forces can also be observed in reversible systems. The careful reader will have noticed that in both models I stated “Throw the die, and note down the number of spots”. Assuming you did so, the evolution in both models can be reversed. Simply start with the last configuration, and instead of throwing the die, read out the written numbers in reverse order, starting with the last one. That's all. The system will reverse its whole history, and when you arrive at the first number, it will be back in its original state.
This is not a unique behavior of the above models. Any system with an underlying reversible micro-dynamics, when generating a macro-scale entropic interaction will do so in a reversible way. This is nothing shocking. Entropic attraction can be observed in molecular dynamics simulations as simple as mixtures of hard spheres of different sizes. Such molecular dynamics simulations are nothing more than ways to solve Newton's equations of motions for large numbers of interacting particles. And as we all know, Newton's equations of motion can be reversed in time simply by reversing all individual velocities.
What next?
The above description makes it clear what is the main task ahead of us: working out what are the right microscopic degrees of freedom that results in the correct entropic gravity. Verlinde's work gives the hope that as soon as we know the correct holographic degrees of freedom, a gravity-free holographic quantum field theory can be constructed that describes gravity in four-dimensional space-time along with electromagnetism and the weak and strong nuclear forces.
I am not too optimistic that we will soon have such a theory. Yet, even in the absence of such a full description, we can still make progress and clarify further consequences of an entropic gravity theory.
In a previous blog post I have made it clear that such a theory unavoidably (and almost trivially) lead to an accelerated universe. Whilst it might not be immediately obvious that clogging together of mass leads to an increase in the number of degrees of freedom, the fact that cosmic expansion leads to increased degrees of freedom should not surprise anyone. A quick calculation shows that the corresponding entropic acceleration is of the right magnitude to describe the cosmic acceleration: d2R/dt2 = 2c2/N dN/dR = 4c2/R, where N represents the number of degrees of freedom of the observable universe (assumed to be proportional to 4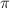 R2, the area of the cosmic horizon). Subsequent work by Li and Wang and Gao, as well as more recent work by a group around Nobel laureate Smoot has corroborated these results. Smoot et al recently also demonstrated entropic effects also hold the potential to explain the postulated primordial cosmic inflation.
R2, the area of the cosmic horizon). Subsequent work by Li and Wang and Gao, as well as more recent work by a group around Nobel laureate Smoot has corroborated these results. Smoot et al recently also demonstrated entropic effects also hold the potential to explain the postulated primordial cosmic inflation.
Inflatons, dark energy: will all of it disappear? Surely, holographic entropy holds the promise of taking up the role of a well-polished Occam's razor!
------------------------------------------------
More Hammock Physicist articles: The largest distance between two points. What you didn't know about E=mc2. Time's arrow. Quantum telepathy. Booting up the universe. Fibonacci chaos. Powers of six-billion. Quantum virus. The grand arena of physical reality. Game theory and the art of acting rational. Holographic hot horizons. Holographic horizons get hotter. How to get rid of dark energy.





Comments