The Principle of Maximal Aging - Capturing the Essence of Relativity

Ever wondered what is the longest path from A to B? I will give you a definite answer in a minute. Stay tuned. 

We first need to go back in our memories and remind ourselves what we learned in physics class. Remember Newton's first law?

Newton's first law: “A free particle moves in a straight line and with constant velocity”

Einstein was not afraid to overhaul our most basic notions of space and time, but he carefully avoided touching Newton's first law. Rather he extended its application domain from three-dimensional space to full four-dimensional spacetime. This allowed for an elegant and compact re-formulation:

Newton's first law for flat spacetime: “A free particle moves in a straight line”

It is thanks to the inclusion of time as the fourth dimension, that the constant velocity requirement can be omitted: it is implicit in the straight line constraint.

Einstein later realized that objects falling in gravitational fields can still be considered 'free' objects. And this meant that Newton's first law should hold not only for objects freely moving in empty space, but also for all free fall motions of objects under gravitational influence. It was just a matter of properly defining straight lines in curved spacetimes.

In doing so, Einstein expanded the application range of Newton's law far beyond what Newton could ever had imagined. Forget parabolic trajectories, forget Kepler's ellipses.

Baseballs move in straight lines away and back to the earth, and the earth moves in a straight line around the sun. It is just a matter of viewing things from the right (4D spacetime) perspective.

Having said that, for curved spacetime Einstein needed an operational definition of what constitutes a straight line. In flat 3D space we have the Euclidean notion of distance, and a straight line from point A to point B can be defined as the path that minimizes the distance between A and B.

When Einstein worked out distances in 4D spacetime, something unexpected happened that is beautiful but at the same time weird. The beautiful thing is that the path length in spacetime turned out to have a direct physical meaning. The length of the spacetime path taken by an object equates to the aging of that object. This indeed is a beautiful concept: the aging you undergo depends on the path you take, but as it equates to the path length, aging is an absolute and objective quantity agreed upon by all observers. A very useful concept in a theory full of relativities!
The weird thing is that using this notion of aging as definition of distance results in straight lines in spacetime being defined not as paths of shortest length, but rather as paths of maximal length!

Putting this all together, Newton's first law in its general-relativistic form reads:

Newton's first law for curved spacetime “A free object takes the path of maximal aging”

I do stretch things a bit when I refer to this 'principle of maximum aging' as Newton's first law. Would this principle be revealed to Newton, there is no way that he would have recognized this as his own first law. But that is what it is: Newton's first law in its most fundamental form. (Actually, we can move to even deeper truths by throwing in some quantum mechanics and things like Feynman path integrals, but prefer to leave this for another blog!)

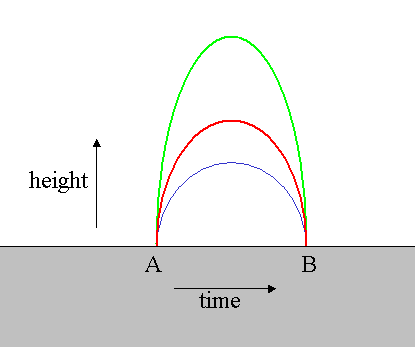
Now let's analyze a simple example, and get a feel for how this all works. Throw a stone vertically up in the air. You observe it move up and down again back to earth. (Make sure you step aside in time!)

Why does the stone follow this particular path?

Don't tell me the force of gravity pulls te stone back to earth. You should know better by now.

Yes, the stone follows the path of longest duration from spacetime event A (launch) to spacetime event B (landing). In this simple example you need to consider only a 2D cross-section of spacetime: make a plot of height versus time, and plot the trajectory of the stone. You observe a perfect parabolic path (red curve in figure).

Wait a second, isn't it obvious that the green path is much longer?

Pardon me? Obvious? You are so indoctrinated by Eulid and his followers! No, the green path is shorter. Issue is that this path is hampered by rapid motions that slow down its aging (remember: if you move fast your wristwatch starts ticking more slowly). In fact, if the velocities along the green path (related to the slope of the green curve in the figure) become too large, the stone would become younger during portions of its flight!

Something seems wrong here. If the red path is longer in terms of aging of the stone, would the blue path not be even longer then?

The answer is again no. The blue path does benefit from the rapid aging associated with slow motion, but fails to avoid the gravitational slowing down of clocks near the earth (remember: your wristwatch moves slower the closer you are to a gravitational object like earth).

But still: this parabola seems so curved. And yet it is plotted in spacetime plot. Didn't you promise us straight lines in spacetime?

You have a point there. However, there is two issues to consider. First, I have highly exagerated the space dimension (height) in this 2D spacetime plot. The point is that whilst the stone travels perhaps a few seconds in time, it is not anywhere near to traveling a few lightseconds in height. So a properly scaled plot would be much wider relative to the height. Secondly, in this properly elongated plot you would need to capture the curvature due to gravitational time dilation. If you modify the plot accordingly, the red curve will appear as a perfect straight line.

If you do the math (which is actually not too difficult), you find that all fits nicely together: the path taken is a parabolic path that carefully compromises between going high to avoid gravitational time dilation, and going slow to avoid velocity related time dilation.


Further reading
Want to learn more about relativity? The book "Exploring Black Holes" by Edwin Taylor and John Wheeler presents General Relativity focussing on the principle of maximal aging. Taylor actually coined the term "principle of maximal aging".

-- And stay away from those rapid aging machines! --