However, there is a limit to how deep you can peek. No matter what equipment you bring, and no matter what part of the electromagnetic spectrum you observe, you can't look back more than 13.7 billion years. What do we see when looking at these times long past? A glow. A nearly uniform microwave glow across the full sky. The cooled-down remnant of the fierce flash of light emitted at the dawn of time.
Visualizing The Big Bang
If you accept these words about the big bang radiation at face value, you are probably not giving them enough thought. Just think for a moment about this radiation surrounding us. Does that make sense? How can we be surrounded by radiation from the big bang 13.7 billion years after the fact? Ignite a bomb, or do whatever you need to do to cause a fireball that emits light and matter. No matter how big a fireball you create, the light will fly out faster than the matter. As a result, observers who are part of the explosion and fly out with the ejected matter, will not keep up with the light and soon not see any of it. So how on earth can we be swimming in the light from the explosion that we ourselves are part of?
Ok, you probably know the reply to this objection: the big bang was not an explosion that happened somewhere. It was an explosion that happened everywhere. Knowing this answer, how do you visualize the big bang? As some giant carpet bombing?
Such visualizations don't make much sense. Any carpet bombing analogy leads to an avalanche of more problematic questions. Who or what orchestrated all these bombs and made them ignite at the same time? And how can it be that the radiation from the big bang is uniform across the sky? Uniformity means each individual bomb in this carpet bombing not only ignited simultaneously, but also each bomb must have been an accurate copy of all the others. Who ordered these zillions of copies of the same bomb, and made them ignite at the same time?
Most pop science books when reaching this point will make some remarks about bombs exploding in space while the big bang creates space. This is the moment in the discussion where galaxies get depicted as raisins in expanding bread dough. Yet, such considerations and analogies do not make the uniformity riddle, referred to by cosmologists as the "horizon problem", go away.
At this point your favorite pop science books will probably introduce the concept of cosmic inflation. As this follows the picturing of our universe as rising bread dough, this leaving the reader with a vague notion of a magical multiplication of dough preceding the baking of the cosmic raisin bread.
If all of this is a reliable description of the big bang theory of cosmology, you should not believe a word of this theory. But of course it isn't. Cosmologists don't need any magical bread multiplication. Forget loafs of bread, forget exploding bombs, forget rubber sheets or whatever you were made to believe represents the big bang. Today, I will present you with a much more satisfying visualization. A visualization that captures the main features of the early universe and that also depicts quite accurately the late stage of evolution the universe has entered. This visualization is relativistically correct, it features an accelerating expansion, and it depicts what is without any doubt the most elegant and most beautiful big-bang model ever constructed.
The visualization will shed new light on the horizon problem, and also suggests an answer to the question "what came before the big bang?". An answer that might surprise you and that at the same time might eliminate any aversion to the big bang cosmology that you might carry with you. And best of all: this relativistic visualization does not require any heavy math. All that is needed is some simple geometrical concepts. The secret to enable this feat is to sacrifice two of the spatial dimensions. This gives us a universe with one time and one spatial dimension that can be visualized as a curled up surface in a 3D space-time.
One last word and a bit of a disclaimer before we start. Is the visualization I will present here the true and unique model of our expanding universe? No it isn't. Firstly, it is an idealized model, and secondly when it comes down to the very early stages of the universe we enter terra incognita. The picture I will present lead us right through the moment of the big bang. Yet, what actually happened at the very moment of the big bang no one can tell for sure. Astronomers can look back down to 380,000 years after the big bang. At the LHC we can recreate the conditions of the universe down to much earlier times of about 0.00000000001 seconds after the big bang. Still earlier times are not experimentally accessible to us, as we lack particle accelerators powerful enough to recreate the energies required. Nobody can claim to know what happened at times and energies not accessible to us. However, we do have theories that go down to much earlier times. All these theories are speculative in nature, and the same applies to below visualization.
I should stress here that regardless of these disclaimers, below visualization honors Einstein's well-tested general theory of relativity, and at the same time it avoids any singularities that would make the math blow up. As such it provides us with an excellent tool to sharpen our intuition when it comes to issues like the horizon problem. The whole point here is: learn from this visualization and use it to sharpen your thinking about issues surrounding big bang theories, but don't get carried away into thinking that this is the last and final word on what happened at time zero.
Having said this, despite the physics at time zero being unknown to us, the big bang phenomenon in itself is not in any way speculative. The fact that our universe is expanding is as certain as the fact that earth's surface is curved. The picture that will be presented below gives a description of the universe akin to the spherical earth description. It provides us with the most symmetric description of our universe: a 'spherical space-time' model. As space-time distances don't behave like spatial distances, a 'space-time sphere' takes the shape of a hyperbolic geometry that enforces a description of an accelerating "open universe". Sounds enigmatic? Read on and all will be clear in a few minutes.
Beauty Bouncing Back
In 1917, just two years after Einstein published his general relativity theory, the Dutch mathematician and astronomer Willem de Sitter came up with a four-dimensional space-time that fitted Einstein's equations. The way he obtained his solution was remarkable: De Sitter had started from a five-dimensional hyper-space-time in which he 'carved out' a four-dimensional hyper-surface at constant distance from a given point.The resulting hyper-space-time sphere, he discovered, satisfied Einsteins equations of general relativity. Amazingly, this solution was obtained in the absence of matter. The space-time that De Sitter had created was purely driven by vacuum energy. Upon hearing of the De Sitter solution, Einstein was convinced this solution could not correspond to any physical reality, and he frantically started looking for errors in De Sitter's calculations. He soon gave up his attempts. De Sitter's math was flawless.

Einstein and De Sitter arguing the intricacies of empty universes
Einstein was shocked by De Sitter's results, as he was convinced that his theory of general relativity embodied his beloved Mach's principle. Loosely speaking, this principle states that dynamics and inertia only exists in relationship to distant stars and all other matter composing the universe. His theory of general relativity stated how matter curved space-time, and how space-time curvature in turn made the same matter move. From a Machian point of view, a most satisfying self-consistent construction. A construction now thorn apart by a solution that contained no masses at all. Einstein was forced to conclude that no matter how valid his gravitational field equations, they allowed for massless solutions and therefore did not embody Mach's principle.
Five years later, in 1923, British astronomer Arthur Eddington and German mathematical physicist Hermann Weyl discovered that the universe described by De Sitter's space-time hypersphere is not static. Rather, De Sitter's equations describe an expanding universe. Einstein, and many others who were convinced they lived in a stable and static universe, immediately brushed De Sitter's model aside as a mathematical artifact. An artifact that unfortunately was contained in the equations for general relativity. Six years later, in 1929, Edwin Hubble published hard evidence that our universe is expanding. By that time De Sitter's work had fallen in disgrace and other cosmological models were available based on Friedmann's and Lemaitre's work that, although less elegant, had the distinct advantage of allowing the effects of mass to enter the model.
De Sitter's model lay dormant for more than half a century. However, as is often the case with beautiful math, it has the tendency to pop-up again and to re-enter physics. Indeed, in the 1980's De Sitter's model bounced back into mainstream physics and cosmology. This time as the key model to describe the very early universe and as a solution to the horizon problem. Finally, the place of De Sitter's model in cosmology got permanently secured when at the very end of the twentieth century it was discovered that the expansion of the universe is accelerating, and that our own universe is inevitably heading for an evolution described by De Sitter's model.
From Minkowski To De Sitter Universes
As mentioned above, we will be constructing a two-dimensional space-time that describes a universe with one spatial and one temporal dimension.How does it feel to live in such a linear universe? Imagine an astronomer living in this narrow linear world. Where we have at our disposal two hemispheres of sky, the full sky available to our linear astronomer consists of no more than two antipodal points. That's all.Two points of light at the opposite ends of a long tunnel of vanishing width. Imagine this astronomer to look deep into both ends of the tunnel. The latest technology available allows the astronomer to observe the deepest light emerging from these two points. The light emitted at the dawn of time. Amazingly, both lights appear to shine with exactly the same intensity and the same color. How can this be? These far-away starting points of the universe can not have been in prior communication with each other, so how can they shine as two copies of the same light?
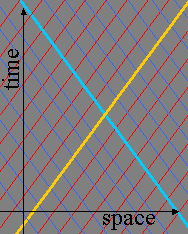
Minkowski's flat spacetime
The astronomer knows relativity theory and is fully aware that in his narrow universe causations are observer-independent and absolute. In a space-time description the causations can be visualized as parallel straight lines. In the above plot these are shown in red (causations from left to right) and blue (causations from right to left) lines. The slope of the lines of causation represents the speed of causation, also referred to as the speed of light, again an observer-independent absolute quantity. Each point in this so-called Minkowski space-time is crossed by two causations, reflecting the fact that any event is the result of causations arriving from the left as well as from the right. One such pair of causations is highlighted with thick yellow and blue lines.
In this Minkowski picture it is quite enigmatic that the left-propagating and right-propagating light emitted at the dawn of time are observed to have the same color. The emission of both light signals at the dawn of time are two separate events the don't share any common cause (see below figure).
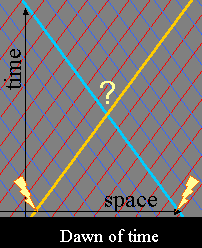
A Minkowski description leaves an observer located at the question mark puzzled how come the two opposing light rays reaching her from the distant past are strongly correlated
Could it be that the space-time our astronomer lives in is not Minkowskian but curved? Curved in such a way that both light rays reaching the astronomer originate from one and the same event? The answer is "yes", this is very well possible. One can build a curved space-time consisting of left- and right-oriented lines of causations that cross each other. What might surprise you is that this can be achieved without bending the straight paths of causation. There is one unique way to achieve this, and it requires us to go one dimension higher than the space-time we want to describe. The curved space-time thus created is again two-dimensional (one spatial and one temporal dimension) and takes the shape of a hyperboloid embedded in a three-dimensional (two spatial dimensions and one time dimension) space-time.
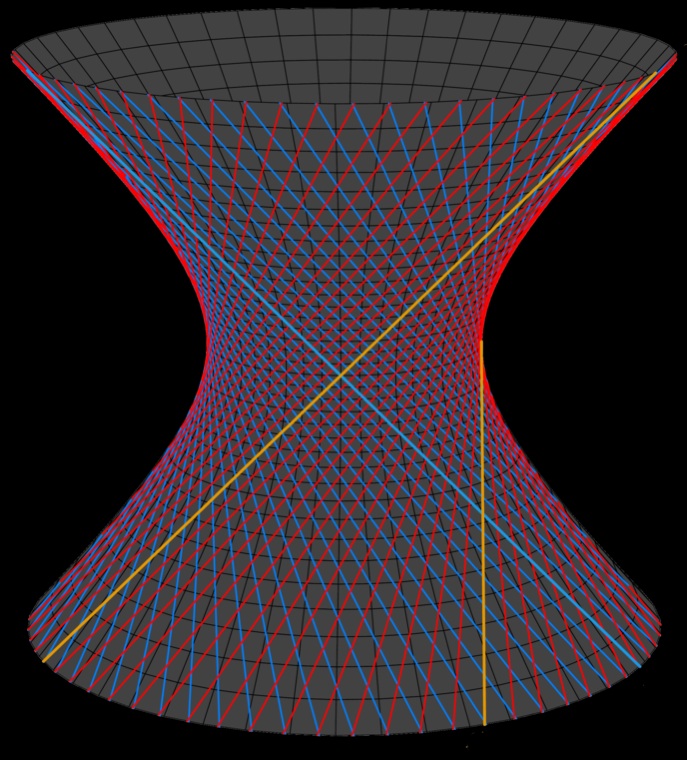
De Sitter universe with one spatial (circumferential) and one time (upward) dimension. This universe is build from straight light paths (red and blue lines) embedded in a 3D Minkowski space-time. This 3D background serves as an aid in visualizing the universe, and is not in any way part of the universe.
This is the De Sitter universe with 1+1 space-time dimensions. The lines of causation (red and blue lines) remain straight, and run without beginning or end. The universe thus created is past and future infinite, and the big bang is replaced by a compact phase: a 'big bottleneck' also referred to as a 'big bounce'. At this bottleneck the universe is hot and dense and opaque to any light. Away from the bottleneck, the universe expands both towards future infinity and towards past infinity.
This is an utterly simple universe model that at one fell swoop eliminates a multitude of issues surrounding big-bang cosmologies. Firstly, there is no singularity plaguing the model. At the 'big bottleneck' the universe attains a minimum size, but at no stage of evolution does the size of the universe drop to zero. Secondly, there is no issue of lines of causation terminating at a time zero. No fine-tuning nor any special boundary conditions are required at time zero. Thirdly, the universe is time-symmetric and therefore fully compatible with the known fundamental laws of physics that are strictly time symmetric. And finally, with this cosmological model the "dawn of time" has disappeared and with it has the horizon problem. More in particular, when tracing back the opposing red and blue light rays arriving at an event in the distant future (and event at a distance from the bottleneck much further away than the bottleneck diameter), one notices that both light rays, when continued through the bottleneck towards time "minus infinity", get arbitrarily close in terms of distances expressed in the local diameter of the universe (the local circumference of the hyperboloid).
Big Bounce, Big Symmetry, Big Speculations
I have argued before in favor of a 'big bounce'. The argument at that time was based on thermodynamic considerations and the need to eliminate the special character of the low-entropy starting point of the universe. Here, the big bounce follows from a search for the most symmetric solution to Einstein's equations. Other speculative approaches such as 'Loop Quantum Cosmology' also point towards big bounce scenarios. It is tempting to interpret these results as diverse hints all pointing towards our universe having bounced 13.7 billion years ago. Although merely a speculation, this is a very tempting speculation.
Some researchers go even further and contemplate whether the ultimate symmetry present in the De Sitter space-time is perhaps directing towards a kinematics more general than the relativistic kinematics derived by Einstein. If it is indeed the case that Einstein didn't go far enough, and modelling the full evolution of our universe requires a new kinematics that goes beyond special relativity, all of modern physics needs to be rebuild... Another subject to be added to the ever growing list of intriguing speculations to be discussed here.





Comments