Still reading?
Ok, I have warned you. Brace yourself. I am going to argue against what many believe to be the most fundamental law of physics. A sacrosanct law. A law that you experience everyday and that is so obviously true that no one should meddle with it. You all know this law. It's the law referred to as 'the second'. The second law of thermodynamics.
Ok, don't blow it hammock guy. You can argue against every concept in physics, but don't touch the second law of thermodynamics! You don't want to place yourself in this group, do you?
Has anyone ever dared to attack the second law of thermodynamics? I am not aware of even a single attempt. Eddington's famous remark on the second law of thermodynamics says it all. This law occupies a special position in physics and rules supreme. Beware the person who dares to meddle with it:
It was Rudolf Clausius, the inventor of the term 'entropy', who already told us that the entropy of the universe* can go only one direction: it can only increase. And once Ludwig Boltzmann and Claude Shannon were done, we became familiar with the true meaning of the term entropy, and it all started to make sense. Entropy simply is the information content of a physical system, the number of digits needed to fully describe the system down to its smallest details. So the second law tells us that the number of digits needed to describe the universe keeps increasing. Seems fair enough, right? The whole universe expands, so probably its information content increases as well.
One-way Universe
Wait a second. Take Newton's laws, or any other fundamental law of physics. All these laws are reversible. They describe a two-way universe. Look at two elastically colliding billiard balls. Now consider the same collision reversed in time. This reverse collision is as valid as the collision going forward in time. Our laws of physics describe a two-way universe. A universe without an 'arrow of time'. This holds for all fundamental dynamical laws, including the las that describe the dynamics of atomic and subatomic particles.Yet, our human experience that focuses on scales much larger than microscopic scales is vastly different. We seem to live in a one-way universe. Glass can brake, but it can't unbreak. You can turn a piece of wood into ashes, but no one has managed to reverse that process. We grow older, never younger. We all can remember the past but not the future.
What is the origin of this arrow of time? Why does time present itself as a one-way road?
Feynman contemplated these issues, and considered them of enough relevance to bring to the attention of undergraduate students at Caltech. In his 'Feynman Lectures on Physics' he points towards the big bang as the cause of the one-way-ness:
Many years later another Caltech physicist and science communicator, Sean Carroll, continues to study the puzzle of entropy increase breaking the two-way nature of our universe:
So the current consensus is that entropy increases simply because there are many more configurations that require a large number of digits to describe them, then that there are configurations described by fewer digits. We all now that with four digits you can describe a total of 10,000 configurations, with two digits only 100. So statistically, a physical system will be likely to end up in configurations described by more digits. But as Sean Carroll stresses, that still leaves the question why the universe started in such a particular low entropy configuration described by very few digits.
Since his 1989 book 'The Emperor's New Mind', Roger Penrose has been drawing the attention of the wider public to the remarkable low entropy of the big bang. In his magnum opus 'The Road to Reality' he revisits the issue, and finally in his latest book 'Cycles of Time' he presents a whole new cosmology aimed at explaining the low entropy beginning of our universe.
In my last blog post I discussed 'Cycles of Time' and made the statement that the big bang must have had a low entropy, but that very fact should not surprise us. The best way to explain this is by studying a simple toy model.
Fibonacci Universe
Imagine a universe much simpler than ours. A universe in which time progresses in discrete steps. At each tick this universe jumps into a new spatial configuration. The physicists living in this universe have managed to describe these configurations, down to their most minute details, in terms of simple numbers. They discover that at a certain step their universe is in a configuration that can be described by the number 4,298,034,510. One tick later the universe is in configuration 6,954,365,922. Then in 11,252,400,432, and next in 18,206,766,354. Scientists study these numbers and try to find a pattern. "If we find the mathematical law that generates these numbers, we will have a theory of everything" they exclaim. "We will know the mind of God!"They readily observe that all numbers are even, and coin this 'the first law'. They also recon that the numbers keep growing, this provides them with their 'second law'. Next they discover how to quantify this growth: each next number appears to be about 1.618034 times the previous number.
Based on experiments in their particle accelerators the scientists start contemplating how the Second Law of configuration number growth would apply to an anti-universe obtained by replacing all particles by anti-particles. It is not before long that theorists come up with a growth rule for anti-universes: each next configuration number in an anti-universe will be -1.618034 times the previous number. The negative sign causes negative configuration numbers to appear, but the second law will still hold as the configuration numbers would not just oscillate but also grow in size. There is a lot of discussion about the meaning of the minus sign in the growth number. However, this discussion subsides when the scientists start realizing that growth laws can only be an approximation to a deeper truth. Simple reason being that a repetitive multiplication by a non-integer number can't produce pure integers. Many scientists frantically try to find out how exactly each integer determines the next. No one succeeds.
Then a young scientist starts toying with the idea that a law that determines the next configuration based solely on the previous one might not exist. Could it be that two or more subsequent configurations are needed to determine the next? He immediately stumbles upon an amazingly simple pattern in which each number is nothing more the sum of the previous two numbers.
This hits the scientific community like a bomb shell.The scientist now realize they were pursuing the wrong approach by assuming the state of the universe requires only one configuration number. So they start considering pairs of subsequent configuration numbers as describing the universe:
It is as if the number of dimensions of the universe they live in have doubled overnight! For reasons no one remembers, the scientist start referring to the space of configurations described by pairs of numbers as the phase space. This to distinguish it from the configuration space that carries only a single number.They next discover that the anti-universe to their own universe is obtained simply by changing the sign of one of the numbers in the phase-space pair. So
would describe the anti-universe of
and vice versa. By applying the 'add-the-last-two' rule to the numbers appearing in subsequent pairs, they can reproduce the observed evolution in terms of the configuration pairs:
and they can do the same for the anti-universe:
A new riddle has appeared. Why do a universe and its anti-partner evolve differently? This can't be right as universes and their anti-universes are related by a simple sign change in the configuration pairs.
It doesn't take long before a bright mind realizes a universe and its anti universe both evolve according to the 'add-the-last-two' rule, but they do so in opposite directions in time.
This means that by knowing a configuration pair, it is not only possible to compute forward in time, but also to trace back the history of their universe. And the amazing thing is: this can be done by using the very same 'add-the-last-two' rule, provided one changes the configurational pair into the corresponding anti-pair and reverses the order of the two numbers in the pair (an operation referred to as time reversal):
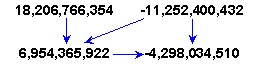
Now all pieces of the puzzle have fallen in place. By transforming universes in their anti universes and back again, the scientists can compute the phase-space state of the universe forward and backward in time. They can now answer the mother of all questions "how did it all start?". So they begin computing back in time. Starting from the pair
they reach lower and lower numbers:
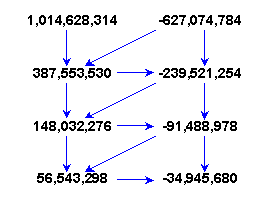
No small task given the rudimentary computational resources in their rather limited universe. But they keep calculating and reach still lower numbers:
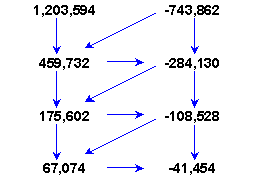
The computations continue further. And further. The numbers reduce in size to 3-digit and then 2-digit numbers. Then something remarkable happens, the numbers start growing in size:
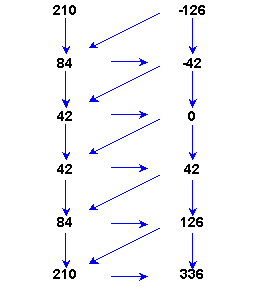
Did they make an error? They check their calculations, and check them again. Everything seems right. What is happening here? Have they stumbled upon an exception to the second law? If the numbers grow in size when going backwards in time, they shrink going forward in time. But the second law forbids this. And this law rules supreme. Or does it?
Big Bounce
Pick a cellular automata rule, take the Hotel Boltzmann dynamics, use Langton's ant, or construct a much more complicated dynamics based on Loop Quantum Gravity. It doesn't matter which model of the universe you create. As long as you create a model that is reversible and that grows without bounds, the very same behavior is observed: a bounce. The bit size of your reversible model universe will go through a contracting phase followed by an expansion phase.The conclusion seems inevitable: if the second law of thermodynamics doesn't hold true for any of these simple model systems, it is probably neither true for our own universe. One could argue that all of this just means the second law of thermodynamics holds true only at one side of the bounce. That would be compatible with the observed entropy increase following the big bounce that we refer to as the big bang.
This is a too restrictive view. It is much more insightful to start from a timeless description and to view an unbound reversible dynamics as a chain of states that never retraces its steps and that therefore has no beginning and no end. In terms of the length of the description of the states (the entropies of the states), such a chain can not be monotonic. The entropy of the states has to feature a bounce. This is inevitable, simply because the length of the descriptions can't drop below zero. With a bounce, the direction of entropy increase at either side of the bounce is pointed away from the bounce. And as low entropy states can not carry the memory of high entropy states, a temporal direction with an unknown future results.**
Where does this leave us with the Second Law? Clearly when expressed a-la Clausius "The entropy of the universe can only increase" does not hold true. However, we can redefine the Second Law such that it does cover the observed bounce behavior:
"The entropy of the universe is a convex function of time."
With S(X) denoting the entropy of the universe in state X, Clausius formulaition of the second law reads:
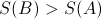if B comes after AThe above findings suggest a replacement of the form:
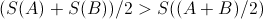for any states A and BIs this the correct formulation of the second law? I don't know. But I do know that when considering model systems, this convexity formulation makes more sense than the standard formulation. Also this new formulation, in contrast to Clausius' formulation, makes no use of an ordering of events, and fits naturally with reversible laws of physics.
An important corollary of a convex function or bounce-description of the second law is that one should not wonder about the smallness of the entropy of our universe about 13.7 billion years ago. If the universe does not retrace its steps, it has to have a minimum entropy at some point. That point we refer to as the big bang, but that should be more appropriately be referred to as the big bounce.
Assuming that the big bang represents a temporal singularity that marks the start of time is an unnecessary assumption. An assumption that gets you in all kind of trouble and forces the question why the starting point was so special and had such a low entropy.
A big bounce seems to me a cleaner description that more easily survives Occam's razor than a big bang singularity. Let's remind ourselves of the fact that there is no single piece of evidence that would make us believe that our universe is in any way bounded, either in spatial extend or in time. For all we know, the universe will keep expanding indefinitely in all directions. Similarly, the universe can extend in both time directions without limit. There is no reason to believe that our universe won't reach everywhere and everywhen.
Only when we know the ultimate theory, will we know for sure the character of the state referred to as the big bang. In the meantime, you have to make a choice in what answer you are going to give to the question "what was there before the big bang?". Will your answer be the traditional
A) "This is a nonsense question, you might as well have asked what is south of the South Pole!".
Or will it rather be a bounce-inspired
B) "An universe that is a mirror universe to our own, consisting of anti-particles moving back in time and mirrored in space."
Faites vos jeux.
Notes
* Throughout this blog post, wherever the term 'our universe' appears, this refers to our observable universe.** I am making some big jumps here that deserve a separate blog post. Note that I am not making any statement on how the laws of physics can lead to memory in conscious beings. No one knows how to make that link.
Comments