Answers to these questions can be found at many places on the internet. However, you can work out all these answers yourself, and in the process learn a few things about the universe. All you need as input is one number. One single number, plus some elementary physics insight in the form of scaling relations. I will give you the number.
Have a pen handy?
Ok, the number you need is 0.00... plus one-hundred-twenty more zeros... followed by the digit 1.
You may want to write this down as 10-123. In fact, as we will deal with lots of numbers scattered over many orders of magnitude, I would suggest from now on you write down just the base-10 exponents of all numbers you encounter. Ok, so you note down the number -123.
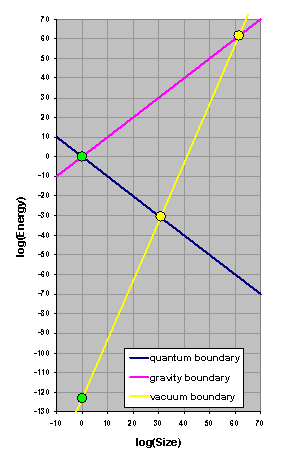
Now take a piece of paper. Draw the axis of a graph, the horizontal axis running from -10 to +70, the vertical axis running from -130 to +70. These numbers also represents exponents in base-10. So both axes are logarithmic with the vertical axis covering a whopping 200 orders of magnitude. (Yes, we'll need that!)
The horizontal axis represents size expressed in Planck lengths, and the vertical axis represents energy also expressed in natural (Planck) units. Now you don't need to worry about how to express Planck units in SI units or any other units of your liking. In fact, it doesn't matter what units you work in. All the physics is captured in ratios, and these do not change when going from one set of units to another. When the size of the universe is two-hundred-gazillion times larger than some subatomic particle, it is so in any set of units. So let's chose Planck units as these make our task much easier. (You will soon see why.)We will mark down two reference points. The first is the point that labels the Planck scale (Planck length and Planck energy). Well, that is easy. As we are working in Planck units, both the Planck length and the Planck energy equal 1 = 100. So both points have base-10 exponent 0, and hence we mark the point (0, 0).
 Now we mark the vacuum energy. The vacuum energy in a Planck-size (100) cube is 10-123 Planck units. So, this is where you need the number you noted down: mark the point (0, -123) in the graph.
Now we mark the vacuum energy. The vacuum energy in a Planck-size (100) cube is 10-123 Planck units. So, this is where you need the number you noted down: mark the point (0, -123) in the graph. You now have two points marked along the vertical axis. In the above figure, I have highlighted these two points with green symbols. Now draw two 45-degree lines away from the point marking the Planck scale. The line going up (shown in purple in above figure) represents the 'gravity boundary'. What happens if this boundary gets crossed? For instance, what happens with an object with a given total energy content (mass energy plus kinetic energy) shrinks in size such that the corresponding point in the plots crosses the gravity boundary? You have guessed it: the object turns into a black hole. So the gravity boundary describes black holes of various sizes.
The line going down (dark blue in above figure) represents the 'quantum boundary': quantum physics (more specifically Heisenberg's uncertainty principle) prevents objects to have size and energy such that these would plot below this quantum boundary.
 Now we turn to the vacuum energy point. Draw a straight line with slope 3 from the vacuum energy point to the upper right (the yellow line in above figure). This line denotes the 'vacuum boundary'. It represents the energy contained inside an empty cubic box of given size. This might seem a very strange concept: “how can vacuum have weight?” The right way to think about this is to consider that the existence of absolute nothingness would mean that within arbitrary small volumes of that nothingness the energy and momentum would be known to be zero. Such an infinite accuracy is incompatible with the quantum mechanical uncertainty relations. The bottom line is that you can not get any physical system at the right-hand side of the vacuum boundary, as this would require you to create a system that is 'more empty' than a perfect vacuum. Quantum fluctuations prevent you from doing so.
Now we turn to the vacuum energy point. Draw a straight line with slope 3 from the vacuum energy point to the upper right (the yellow line in above figure). This line denotes the 'vacuum boundary'. It represents the energy contained inside an empty cubic box of given size. This might seem a very strange concept: “how can vacuum have weight?” The right way to think about this is to consider that the existence of absolute nothingness would mean that within arbitrary small volumes of that nothingness the energy and momentum would be known to be zero. Such an infinite accuracy is incompatible with the quantum mechanical uncertainty relations. The bottom line is that you can not get any physical system at the right-hand side of the vacuum boundary, as this would require you to create a system that is 'more empty' than a perfect vacuum. Quantum fluctuations prevent you from doing so.Why did we draw the vacuum boundary with slope 3? The reason is that the vacuum energy within a given volume is proportional to that volume. And as volume scales with the third power of the linear size, the vacuum boundary is represented in the figure as a line with slope 3. You can not get any physical system at the other side of this boundary, as this would require you to create a system that is 'more empty' than a perfect vacuum.
Look at the figure you just created. The three straight lines drawn form a triangle. This is the grand arena of physical reality. It entails all known physics, from the smallest possible (Planck length) scales, to cosmic length scales spanning the whole observable universe.
 What defines the corners and edges of this grand triangle? Well, the point (0, 0) where the gravity horizon crosses the quantum horizon is easy. This point is defined by the Planck scale. We know very precisely the location of this corner, but we have no clue what physics it represents. It is the corner of the triangle that is governed by the yet-to-be-found 'theory of everything'. This theory requires a merger of the laws of gravity (general relativity) with the laws of quantum physics. Many believe that string theory will provide such a merger, others claim that loop quantum gravity will disclose this corner. The truth is that despite huge efforts and many, many years of research by the brightest theoretical physicists, we still have no clue how to combine the laws of gravity with the principles of quantum physics. The Planck corner of our triangle is a big mystery and is likely to remain so for a while.
What defines the corners and edges of this grand triangle? Well, the point (0, 0) where the gravity horizon crosses the quantum horizon is easy. This point is defined by the Planck scale. We know very precisely the location of this corner, but we have no clue what physics it represents. It is the corner of the triangle that is governed by the yet-to-be-found 'theory of everything'. This theory requires a merger of the laws of gravity (general relativity) with the laws of quantum physics. Many believe that string theory will provide such a merger, others claim that loop quantum gravity will disclose this corner. The truth is that despite huge efforts and many, many years of research by the brightest theoretical physicists, we still have no clue how to combine the laws of gravity with the principles of quantum physics. The Planck corner of our triangle is a big mystery and is likely to remain so for a while. The part of the triangle boundary we know best is the part represented by the blue line away from the Planck area. This is the realm of quantum physics. Electromagnetic waves ranging from ultra hard gamma rays to less hard gamma rays, ultraviolet and visible light, and finally microwave radiation, bring us along this quantum boundary from the Planck scale to the yellow point at the bottom. This is the path followed by the photons created at the big bang. These photons reach us in the form of cosmic microwave background radiation. The yellow point at (30.75, -30.75) denotes the reduced wavelength and energy of the photons that constitute this microwave background.
The part of the triangle boundary we know best is the part represented by the blue line away from the Planck area. This is the realm of quantum physics. Electromagnetic waves ranging from ultra hard gamma rays to less hard gamma rays, ultraviolet and visible light, and finally microwave radiation, bring us along this quantum boundary from the Planck scale to the yellow point at the bottom. This is the path followed by the photons created at the big bang. These photons reach us in the form of cosmic microwave background radiation. The yellow point at (30.75, -30.75) denotes the reduced wavelength and energy of the photons that constitute this microwave background.
 As already mentioned, the purple edge depicts the mass-size relationship for black holes. Away from the Planck scale, the behavior of black holes is well understood. This behavior is governed by Einstein's general theory of relativity. Closer to the Planck corner, we are less certain. The nearer to the Planck scale, the more enigmatic black holes behave. In fact, closer to the Planck scale we deal with quantum objects that can hardly be labeled 'black holes': these ultra-dense quantum objects evaporate by sending out radiation at wavelengths roughly comparable in size to their circumference.
As already mentioned, the purple edge depicts the mass-size relationship for black holes. Away from the Planck scale, the behavior of black holes is well understood. This behavior is governed by Einstein's general theory of relativity. Closer to the Planck corner, we are less certain. The nearer to the Planck scale, the more enigmatic black holes behave. In fact, closer to the Planck scale we deal with quantum objects that can hardly be labeled 'black holes': these ultra-dense quantum objects evaporate by sending out radiation at wavelengths roughly comparable in size to their circumference.
 Moving along the gravity boundary towards the top right-hand side we move to larger and larger black holes. Finally we reach the corner of the triangle at the point (61.5, 61.5). This point marks the radius and total energy content of the observable universe. The fact that this point is at the boundary describing black hole behavior, suggests that our universe is close to the threshold of collapsing. Well, that would be the case, were it not that a significant portion of the energy content of the universe is dark energy. This dark energy behaves as if it is ruled by laws of anti-gravity, and creates a repulsive force that seems to create an accelerating expansion of the universe.
Moving along the gravity boundary towards the top right-hand side we move to larger and larger black holes. Finally we reach the corner of the triangle at the point (61.5, 61.5). This point marks the radius and total energy content of the observable universe. The fact that this point is at the boundary describing black hole behavior, suggests that our universe is close to the threshold of collapsing. Well, that would be the case, were it not that a significant portion of the energy content of the universe is dark energy. This dark energy behaves as if it is ruled by laws of anti-gravity, and creates a repulsive force that seems to create an accelerating expansion of the universe.That brings us to the yellow boundary in the figure. The vacuum energy line. In the triangle this line is opposite the Planck corner. That would suggest that this is part of the triangle that is best understood. Nothing could be more besides the truth. In some mysterious way, the combined effects of quantum physics and gravity conspire to create this vacuum energy. The fact that there is such a vacuum energy line is not surprising. What is surprising is the position of this line in the graph. Based on general quantum physics considerations, one would expect such a vacuum energy line to cross (or get near to) the Planck point. Yet, in the triangle of physical reality the vacuum energy represents the boundary furthest away from the Planck corner.
All-in-all, we have absolutely no clue why the vacuum energy is characterized by the absurdly small value of 10-123. This value is not backed up by theory. It simply is a value derived from the observed acceleration in the Hubble expansion of the universe. This also means that we have no clue why the yellow line crosses the quantum boundary at the point that characterizes the remnants of the big bang: the microwave background radiation (the lower yellow dot). If you ask a cosmologist why the vacuum energy at lengths comparable to the reduced wavelength of the cosmic microwave background photons equals the energy if these photons, you most likely get the answer that it is just a coincidence. In a future article I will come back to this issue, and present some evidence that the cosmic repulsion driving the accelerated expansion of the universe might in fact be completely unrelated to vacuum energy. But let's not go into these puzzles. For the purpose of creating a visual overview of the arena of physics, we go along with the generally accepted view that the cosmic expansion is due to a vacuum energy. So let's go back to our triangle.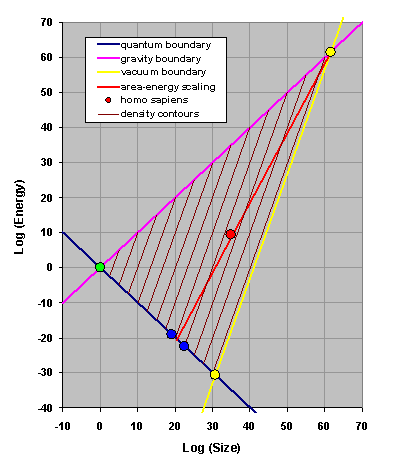
We zoom in a bit. In this zoomed-in view I have included density contours (thin lines parallel to the vacuum boundary, with each contour line representing a factor 10 billion jump in density), as well as a red line and some additional symbols. The red line is the line with slope 2 drawn through the point representing the observable universe. As this red line is in between the purple line with slope 1 and the yellow line with slope 3, it should be clear that this red line is the only line with integer slope that crosses the triangle and goes through the corner describing the universe. This line can be thought of as an area-energy scaling: objects of different sizes but with an energy:area ratio corresponding to that of the observable universe fall on this line. Remarkably, this line crosses the quantum boundary exactly where the known subatomic particles are located. (The blue dots shown represent the electron and the proton.) So in terms of areal density, the smallest known objects (subatomic particles) are no different than the largest know object (the observable universe).
 And then there is this red dot in the middle, also described by the same area-density scaling. Positioned at (35, 9.5) it interpolates between subatomic particles and the scale of the universe. It is a slow-moving lazy object, with virtually all of its energy contained in mass. That is a mass of 109.5, more than a billion and less than ten billion Planck masses. Yet, due to its large size (1035 Planck lengths), it is characterized by a very low mass density of 10-95.5. Obviously, this is an ultra-sparse object that surely would not have existed if the vacuum density would not have been even smaller than this low density.
And then there is this red dot in the middle, also described by the same area-density scaling. Positioned at (35, 9.5) it interpolates between subatomic particles and the scale of the universe. It is a slow-moving lazy object, with virtually all of its energy contained in mass. That is a mass of 109.5, more than a billion and less than ten billion Planck masses. Yet, due to its large size (1035 Planck lengths), it is characterized by a very low mass density of 10-95.5. Obviously, this is an ultra-sparse object that surely would not have existed if the vacuum density would not have been even smaller than this low density.
So what is this ghost type object in the middle of the arena of physical reality?
It is a living creature. From its central position it manages to look deep into the universe up to the top right hand corner of the triangle, and at the same time it is capable of studying the very small world along the quantum boundary at the bottom.
It is you.
So after all, could it be that the splendor of the whole universe at all its length scales does center around you? Are you median, rather than mediocre?
------------------------------------------------
More Hammock Physicist articles: The largest distance between two points. What you didn't know about E=mc2. Time's arrow. Quantum telepathy. Booting up the universe. Fibonacci chaos. Powers of six-billion. Quantum Virus.





Comments