The paper is titled "The Probable Fate of the Standard Model". Here, contrarily to what is fashionable nowadays, rather than predicting the demise of the Standard Model because of the discovery of this or that brand of new physics unexplained within its boundaries, the authors consider whether the SM can survive a precision measurement of the Higgs mass, given the fact that only a narrow range of mass values allows the SM to work at arbitrarily high energies.
The theoretical arguments at the basis of the study are not trivial to understand, and even less trivial to summarize to non-experts. I honestly think it is above my head to provide an explanation below (or above) the graduate student level, so I will just provide a "summary for experts", whatever that may mean. However, some of the conclusions I report on at the end might be readable by all.
Aim of the study
The authors start by recalling the theoretical shortcomings of the Standard Model, in particular the need to fine-tune the Higgs mass, but they make it clear that they are not challenging the model on that ground:
"There are, of course, plenty of theoretical arguments why the Higgs sector of the SM is inadequate, many of them related to the apparently unnatural fine-tuning of its parameters, but we have in mind a more direct empirical argument based on the available experimental information about the Higgs sector".
What they set out to do is to examine in the light of the "available experimental information" the theoretical boundaries within which the Higgs mass must lie in order to allow the SM to be a good theory of Nature at any energy scale. The first boundary is given by vacuum stability bounds of the Higgs potential: as the energy scale at which the model is tested increases, these bounds become tighter, and basically allow the SM to be valid for all energies up to the Planck scale (set at
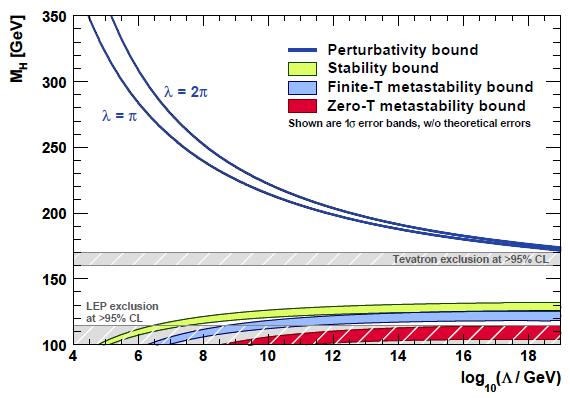
The boundaries are shown in the figure below, taken from the paper. You can see as a function of the logarithm of the energy scale Lambda at which the SM is supposed to be a valid, perturbatively-calculable theory, the range of Higgs masses which make this possible.
A Higgs mass close to the LEP II lower limit runs into trouble at high energy, when the Higgs potential may develop additional minima which can be reached by quantum tunneling, depending on the temperature of the Universe. The green area shows the lower bound and it is not a narrow line because of uncertainties in the calculation. The blue and red areas are more stringent bounds below which metastability occurs. At high Higgs masses, instead, two different blue lines mark the fuzzy boundary of the region where perturbative calculations are enabled or prevented by the size of the Higgs boson self-coupling. Also shown in the figure are direct search limits, in grey.
 The recent precise measurement of the top quark and W boson masses, together with the machinery of global fits to Standard Model observables (most of which are still those determined by LEP and SLD in the nineties) and with the direct limits on the Higgs mass coming from LEP II (
The recent precise measurement of the top quark and W boson masses, together with the machinery of global fits to Standard Model observables (most of which are still those determined by LEP and SLD in the nineties) and with the direct limits on the Higgs mass coming from LEP II (Results of the study
The results of the analysis of all experimental inputs are nicely summarized in another figure (below), which presents the probability that current data give to different scenarios, as a function of Higgs mass. Here, the behavior of the Higgs potential at infinitely high energies is considered, to check whether the SM can or cannot be valid at any energy scale. The red region is the one where the Higgs potential is liable to become unstable in time scales shorter than the age of the Universe; the blue one marks situations where the quantum tunneling out of the ordinary minimum of the Higgs potential is slow enough to make it an acceptable solution; the dark green area shows a situation where the Higgs potential is stable against thermal fluctuations defined by the Planck scale; and the light green area is the solution which makes the SM a candidate for a theory that survives to the Planck scale untroubled by changes of behavior of the Higgs potential or by non-perturbativity of the Higgs coupling. The grey area is the region which makes the theory non-calculable at high energy.
Finally, overlaid with those areas, is the computed value of the probability of Higgs boson masses, extracted by the most recent experimental inputs as discussed above.
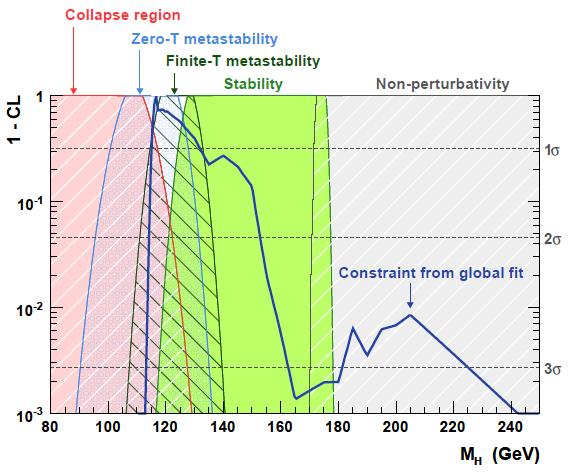
It transpires that there is a wide chunk of green in a region where the blue curve has respectable values of probability (1-CL). The authors compute that the probability that the Higgs mass lies in a region where the Higgs self-coupling becomes non-perturbative at high energy (the grey area on the right) is less than 1%: this is an important addition to our understanding of the limitations of the Standard Model, because the "blowing up" of the Higgs self-coupling has at times been cited as one of the potential shortcomings of the Standard Model at high energy, and a reason for believing that new physics should set in at energy scales well below the one of quantum gravity.
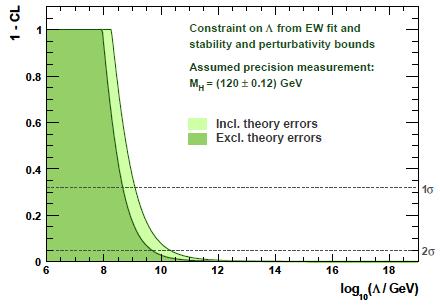
Another point to make from the figure shown above is that the highest probabilities match with a region where it is not perfectly clear whether the Higgs potential is well-behaved in the ultraviolet regime. Because of that confusion at low masses, the authors consider two specific scenarios in the second part of their paper, where the Higgs mass is thought to be measured by a long LHC run at 115 or 120 GeV, with a small (0.1%) uncertainty.
In such scenarios, one could indeed conclusively prove that the Standard Model has to break down at energy scales well below the Planck scale! Take for example the case of
In Summary...
The authors note in their conclusions that:
"the present data exhibit no clear preference between scenarios in which the SM survives up to the Planck scale, and in which it develops new minima at a scale Lambda and becomes metastable with respect to either thermal or zero-temperature fluctuations."They finally make the point that the
"discovery of the Higgs boson might reveal quite conclusively the possible fate of the Standard Model. For example, if the SM Higgs boson were to be discovered with a mass of 120 GeV, the effective potential of the SM would develop a new vacuum at log_10(Lambda/GeV)<10.4 and remain in a metastable state, unless new physics beyond the SM intervenes."All in all, I found this study a fresh new look at data we have seen and scrutinized for quite a few months by now. The point that a discovery of the Higgs boson at specific values of mass may prove that the SM is bound to break down, rather than making it even a greater, unsinkable success, is remarkable. The SM might be sentenced to death by the discovery of the very particle which crowns it!





Comments