The conservation of energy is an insight that stood the test of time. It was Julius von Mayer who first worded it in its clearest form: "Energy can be neither created nor destroyed". That was nearly 170 years ago.
So why question energy conservation?
The interesting thing about physics is that the deeper you dig, the more you are forced to doubt existing principles. Dig deep into the universe, allow gravity to become a dominant feature, and the conservation of energy becomes much less obvious.
Recently, several physics bloggers have tackled the issue of how energy conservation plays out at cosmic scales. You might be surprised to hear that they all seem to conclude that at cosmic scales, total energy can be created and destroyed. Sean Carroll at Cosmic Variance comes to the conclusion:
"it’s better to [..] just admit that energy is not conserved"Sascha Vongehr here at Science 2.0 does not agree with Sean's particular wording, but reaches the same conclusion:
"Energy conservation just does not hold in general relativity"I think they are both wrong. Energy is conserved also at cosmic scales, but one has to look at it from the right perspective. Trying to define the total energy of the universe in the conventional way in terms of a volumetric addition gets you quickly in all kinds of difficulties. The total energy can not be defined as the sum of energies of many small subvolumes. Key to this problem is that there is no such thing as 'the density of gravitational energy'. Gravitational energy is non-local. Or more precisely: it is holographic in nature.
To get a handle on the holographic nature of gravitational energy, we first need to understand the concept of space-time horizons.
From black hole horizons to cosmic horizons
In a recent post I elaborated on what could be referred to as a Bohr model of black holes. The picture that emerged is the following:
A black hole can be described purely in terms of its horizon. For an outside observer this horizon can be thought of as a spherical surface along which a large number of photons move at the speed of light. The number of photons is proportional to the surface area of the sphere, and each photon has energy proportional to the curvature of the sphere or, in other words, an energy inversely proportional to the circumference of the sphere. Multiplying the number of photons with the energy per photon, it follows that the total energy of the horizon, and thereby the total mass or energy content of the black hole, is proportional to its circumference. Working in natural units, this proportionality works out as:
Black Hole Horizon Energy = Horizon Circumference / 4
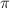
The right-hand side, the horizon circumference divided by 4pi, we will refer to as the horizon half-radius, or HHR.
Outside observers experience the horizon as a boundary from beyond which light can not emanate. This is what makes a black hole 'black'. Light emitted by an object approaching the horizon, can reach distant observers, but experiences difficulty in doing so. This difficulty manifests itself as a redshift that increases as the object approaches the horizon. The closer to the horizon, the more stretched the light that reaches distant observers. At the horizon the redshift becomes infinite, the light from the object stretches to infinite wavelength, and the object disappears out of sight.
So a black hole horizon can be interpreted as a limiting boundary to the region of space that we can observe. The region of space from which photons can reach us with finite redshift.

A cosmological horizon bounds the universe observable to us. The closer an object is to this horizon, the more red-shifted it will be.
But we have another such boundary: our cosmic horizon. The boundary that delimits the part of the universe observable to us. The closer galaxies are located to this cosmic horizon, the more they are redshifted. Right at the cosmic horizon, the redshift becomes infinite. This cosmic horizon, just like a black hole horizon is a spherical surface. It encloses our 'look-back universe'. The observable history of the universe. The HHR of the observable universe expressed in natural units measures a whopping 1061 (yes, that's a one followed by sixty-one zeros...).
And now comes the key point: if we associate with a black hole horizon an energy equal to its HHR or half-radius, then we have to associate a similar energy to the cosmic horizon. But... this cosmic horizon energy carries a minus sign. There is several ways to make plausible the cosmic horizon energy must have a sign opposite to black hole horizon energies. The easiest way is to recognize that the cosmic horizon is curved towards us rather than away from us like black hole horizons. So the total energy of the cosmic horizon, the horizon area times its curvature, carries a negative sign due to its curvature having a sign opposite to that of black holes.
Another way of expressing this is by saying that the cosmic horizon is a black hole horizon turned inside-out. Some prefer to refer to such a horizon as a white hole horizon. This all becomes rather vague and suggestive wordplay. For the present purpose you should just accept the fact that the cosmic horizon that we observe 'from the inside' and black hole horizons that we observe 'from the outside' carry opposite signs when it comes to determining their energy.
With this, all cosmic-scale energy conservation issues have all evaporated. It is the energy associated with the cosmological horizon that fixes the bookkeeping of the total cosmic energy. We have already determined the size of the HHR of the universe, so we know the energy of the associated horizon:
Cosmic Horizon Energy = - HHR = -1061 Plancks
The total mass in the observable universe (including non-luminiferous matter) is about 2x1053 kg or 1061 Plancks. So the total energy of the universe adds up to
Energy of universe = mass energy + horizon energy = 1061 - 1061 = zero zilch nada...
Credits and debits add up to zero. That is how it was at the very start, and that is how it is now. Our cosmos has its bookkeeping in perfect balance.
Expanding baby universes
The fact that the total energy is not just conserved, but more specifically conserved such that it adds up to zero, is essential when considering the origin of the universe. The universe was born in an infinite flash of light. And it will probably also end in a flash of light. Can we model this evolution based on the above derived horizon description? The answer is "yes", and it is surprisingly easy to do.
We don't have a theory that describes Planck-scale physics, but we can make an educated guess on some key aspects of the big bang by audaciously extrapolating the above horizon description to the Planck scale origin of the universe.
The universe started hot. Imagine an infinite space filled homogeneously with ultra-hot thermal radiation. Infinitely many photons with energy close to the Planck energy. Our early universe constituted a tiny fraction of this infinite space. How tiny? We extrapolate back to a universe containing just a few (say three) photons and a total energy content of one Planck. For this baby universe to have sprung out of nothing without violating total energy conservation, it must have a vanishing total energy and therefore an HHR of one balancing the energy content of one Planck. Only a very tiny three photon universe fits into such a half radius. Notice that another observer at a slightly different location in the infinity of space experiences an entirely different universe, also containing just a few photons. Each of these infinite number of baby universes has total energy zero.

The all-too-familiar expanding balloon analogy explaining cosmological redshift: radiation stretches to larger wavelengths due to the expansion of the universe.
How did one of these tiny and dull few photon baby universes grow into the present grandiose display we call our universe? The secret is expansion. Things get more interesting and the number of features grow as soon as the baby universes starts expanding. The wavelengths of the photons as well as their mutual distances increase, and the baby universes grow into larger universes that start to overlap. When the photon wavelengths and inter-photon distances have increased to twice their original sizes, the baby universes have increased their HHR to four times their original value. As a result, each baby universe has grown to 43 = 64 times its original size and now contains 23 = 8 times as many photons.
Does energy conservation still hold?
Let's check this. Each photon has doubled its wavelength and thereby halved its energy. Eight times as many photons at half the energy adds up to four times the energy content in each baby universe. The HHR of each baby universe has quadrupled, and therefore the horizon energy of each baby universe has quadrupled as well into minus four Plancks. Four Plancks of photon energy added to minus four Plancks of horizon energy: the total energy of these baby universes still adds up to zero.
We conclude that for each factor of two expansion, the universe grows a factor of four. In other words: for a given expansion factor, the boundary of the observable universe must have receded away from it's observer by a factor equal to the square of the expansion factor.
A one-third Planck energy baby-universe photon has wavelength equal to 6pi (again in natural units). Expand this wavelength by a Hubble expansion factor of 3 1030, and you get a wavelength of about 6 1031 Planck lengths or about 1 mm. That is the central wavelength of the cosmic microwave background (CMB), the remnant of the big bang. The universe itself is much larger than the Hubble expansion times the size of the baby universe. According to the above, the universe's present HHR should be equal to the size of the baby universe times the square of the Hubble expansion factor.
Let's see if that works out OK. An initial HHR of one times 3 1030 times 3 1030 gives a HHR of 1061. You have seen that number before: it is the observed HHR of our current universe.
Let's recap what we did. We introduced the concept of a horizon energy, a quantity proportional to the circumference of the horizon. With nothing more than this and the law of total energy conservation, we described the Hubble expansion including the redshift of the big bang photons.
Impressive?
Well, I have to admit that I have somewhat reverse-engineered the above derivation. Would I have started with baby universes containing different numbers of photons, or photons at different energy, things would have worked out less precise. Key point, however, is that using a simple horizon energy picture, one can understand the energy balance that leads to zero total energy, and also grasp the expansion of a radiation-dominated universe. The same horizon picture can be used to also derive the expansion of a matter-dominated universe (the size of which increases with the 3/2th power of the expansion factor).
So when asked "is it possible to build a perpetual motion machine that generates energy?" you know what to answer. You reply: "Such a machine would perhaps be possible, but only if you are able to extend it beyond the cosmic horizon." An answer that will leave them in utter confusion and probably shut them up. If they are witty enough to ask the follow-up question "how far away is that horizon?", you reply "not that far actually, the square root of that distance is roughly the wavelength of the light from the big bang, and that's about a millimeter". Never destroy their hope.





Comments