The argument against the splitting of a black hole is elegant in its simplicity. It is based on a geometrical interpretation of black hole thermodynamic properties such as black hole energy and black hole entropy. The reasoning is most straightforward for Schwarzschild black holes. From perspective of a stationary external observer these are nothing more than spherically-shaped glowing gravitational horizons. Whatever is behind these horizons, it is no part of his/her observable universe. As is well-known, all thermodynamic properties of the black hole can be expressed in terms of horizon parameters. The total energy content of a black hole can be identified with the horizon circumference, and the total entropy with the horizon's area. This means that in terms of black hole horizons, the first law of thermodynamics (energy conservation) manifests itself as conservation of circumference, and the second law (entropy non-decrease) as non-decrease of surface area.
And the thing is: you can create multiple smaller spheres such that their total circumference is equal to that of a given sphere, but you can do so only by generating a total surface area that is smaller than that of the original sphere. Mathematically this translates into the statement that the set of equations
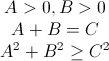
does not allow for solutions. Geometrically this means that starting with three edges with one being the sum of the two others, you can not build a triangle with none of the angles exceeding 90°. This is immediately obvious as out of the edges provided you can build only a degenerate triangle with one angle equal to 180°.
The conclusion is that the splitting a black hole is thermodynamically forbidden. No matter what tools you bring, you can not cut, crush or crumble a black hole.
Unless..
It Takes Two To Tango
Unless you throw at the black hole... another black hole. You can't split a single black hole, but it is easy to see that no law of thermodynamics forbids the splitting of a pair of black holes in three or more components.
To explore the threshold at which splitting becomes thermodynamically feasible, we focus on reversible collisions. This means we try to find black hole collisions that don't lose or produce entropy and that can be played back and forth in time without violating the laws of thermodynamics.
To make this a nice recreational math exercise, we define Schwarzschildean multiplets. First, recall that Pythagorean multiplets (C; A1, A2, .. , An) are defined as sets of integers satisfying the equation C2 = A12 + A22 + .. + An2. An example being the triplet (5; 4, 3). Analogously, we define Schwarzschildean multiplets (C1, C2; A1, A2, .. , An) as whole number solutions to the set of equations
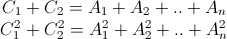
Such a Schwarzschildean multiplet describes a reversible collision between black holes with masses C1 and C2 into n black holes with masses A1, .. , An.
It is easy to see that Schwarzschildean multiplets do exist. The trivial case (1, 1; 1, 1) is obvious, but represent an elastic collision between two black holes rather than a splitting of black holes. The smallest non-trivial case (3, 3; 4, 1, 1) is a valid Schwarzschildean multiplet that does describe a genuine splitting. It tells us that two black holes of mass 3M can in principle collide and split into three black holes of mass 4M, 1M and 1M.The Schwarzschildean multiplets (1, 1; 1, 1) and (3, 3; 4, 1, 1) can be extended to more complex cases: (13, 13; 16, 9, 1), (21, 21; 25, 16, 1), and so on (do you see the pattern?). All of these describe the splitting of two equal mass black holes into three.
Spray Collisions
Is the splitting of two black holes into more than three black holes thermodynamically allowed?
The answer is 'yes'. In fact, the laws of thermodynamics allow two black holes to split into arbitrary many black holes. This can be inferred from the fact that the Schwarzschildean multiplet (3, 3; 4, 1, 1) can also be extended to multiplets (6, 4; 7, 1, 1, 1), (10, 5; 11, 1, 1, 1, 1), etc. (again there is a pattern...) Such multiplets represent 'spray reactions' between two black holes resulting into one large black hole and a shower of small black holes.
It becomes clear the possibilities are almost endless. Effectively, a black hole colliding with a much larger black holes is allowed to split and fragment in any number of small black holes as long as the large black hole grows sufficiently larger in the process.
One final question. The above spray reactions are between a pair of black holes of unequal mass. Is it also possible to have two black holes of equal mass produce unlimited numbers of black holes?
Also here the answer is 'yes'. This follows directly from the fact that when considering Schwarzschildean multiplet describing the collision of two equal mass black holes. You can turn any such multiplet describing the production of k black holes into a multiplet describing the production of one more black hole. More specifically, if (M, M; m1, m2, .. , mk) is a valid Schwarschildean multiplet, then so is (3M, 3M; 4M, m1, m2, .. , mk). Starting from the trivial multiplet (1, 1; 1, 1) and using this recursion relation, one can generate multiplets describing the collision of an equal mass pair into two, three, four, and ever more black holes: (1, 1; 1, 1), (3, 3; 4, 1, 1), (9, 9; 12, 4, 1, 1), etc.
True spray reactions between two equal mass black holes can also occur. We define these as collisions described by a multiplet of the form (m, m; M, 1, 1, .. , 1). The multiplets (1, 1; 1, 1) and (3, 3; 4, 1, 1) can be viewed as i=1 and i=2 cases of a chain of multiplets (mi, mi; Mi, 1, 1, .. , 1) created by starting from these two cases using the simple recursive equations: mi = 6 mi-1 - mi-2 - 2, and Mi = 6 Mi-1 - Mi-2 - 2. This generates multiplets (15, 15; 21, 1, 1, 1, 1, 1, 1, 1, 1, 1) and so on. The iteration leads to exponentially growing shower reactions, with deep iterations describing 29.3% (a fraction 1-sqrt(1/2)) of the total mass being converted into a spray of arbitrarily small black holes.
Milky Way-Andromeda Cataclysm
Our Milky Way galaxy is on a head-on collision course with Andromeda. Both galaxies will merge, and both galaxies harbor a supermassive black hole a their centers. The black hole in our Milky Way weighs in at 4.2 million solar masses, and the black hole in Andromeda has grown into a true giant containing 100 million solar masses. What will happen to these black holes during and following the galaxies merger?
A similar but much smaller merger likely happened a few million years ago. The satellite galaxy that merged with our galactic core carried a much smaller (probably a several thousand solar masses) black hole. Both black holes almost certainly have found each other, and all signs indicate the fireworks that resulted must have been spectacular.
When Andromeda merges with our galaxy, it brings a 10,000 times heavier black hole. It is commonly assumed that ultimately this black hole and our own central black hole will meet. Applying the above 'multiplet math' to the collision of both supermassive black holes tells us that in theory the vast majority of the 4.2 million solar masses contained in the supermassive black hole in our Milky Way could transform into a shower of many millions or billions of black holes. Not a pleasant perspective.
So...
... do you believe all of this?
Surely, the laws of thermodynamics do not forbid these black hole showers. But are these physical? Does all of the Schwarzschildean multiplet stuff represents true physics or is it nothing more than 'frolicking with numbers'?
I hope one of you will put the correct answer in a comment below. Failing that, my next post will be dedicated to the physical reality of black hole collisions producing showers of mini black holes.
Follow-up blog post: here.
–––––––
More Hammock Physicist articles on black holes:
How to count a black hole, Cosmic flash memory, Black hole in our backyard?, Quantum galaxy: NGC 1277.
Comments