So, is it or is it not possible? Can black holes be split?

In my last blog I demonstrated that the laws of thermodynamics forbid the splitting of a single black hole. However, I also demonstrated the same laws don't forbid the splitting of a pair of black holes into many.

This leaves the door wide open for splitting black holes by smashing them together.

Or does it?

I got some good reactions to my 'splitting black holes' blog post. I am happy to see that most of the Hammock Physicist readers who reacted consider such a process, although thermodynamically not forbidden, still to be deeply unphysical. You guys are doing better than the commenters at Physics Stack Exchange! Over there, the claim that multiple black holes can be split went unchallenged.

The conclusive argument against black hole splitting is surprisingly simple and provides us with a nice instance of the thoughts behind a given law being more useful than the law itself.

A simple example will make it perfectly obvious that the second law of thermodynamics (the requirement of entropy non-decrease) is only part of the story.

Colliding Trays

Imagine trays containing colored balls. Let's say we have two trays: one containing eight slots filled with four red and four yellow balls, and another tray with the same number of slots filled with four green and four blue balls. We smash these trays together. This leads to a chaotic process in which the balls redistribute over the trays. Suppose the outcome is one tray filled with four red and four green balls, and the other tray with four yellow and four blue balls.

Would you be surprised?




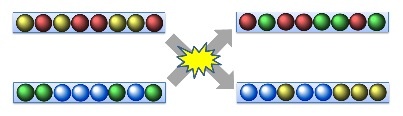
Of course you would be. Yet, I could come up with the argument that the entropy has not decreased. There are a number of ways (70 ways, to be precise) to distribute an equal number of balls of two contrasting colors over eight slots. This count is obviously independent on the choice of colors, as long as these provides a means to distinguish the two groups of balls. Therefore, the initial state can be realized in 70x70 or 4,900 ways, and the final state can be realized in exactly the same number of ways.

With entropy being nothing else than the logarithm of the number of realizations compatible with the large-scale physical description of the system, it follow that the entropy has not changed. Before, as well as after the collision, the entropy is given by Ln(4,900) = 8.5.

As the entropy hasn't decreased, I can argue that the outcome of the collision is in accordance with the second law of thermodynamics, and is therefore entirely feasible.

This, obviously, makes no sense.

This simple example makes it immediately clear how to resolve the issue. Key is that the entropy of the post-collision state could have been much higher. In fact, distributing four red, four green, four blue and four yellow balls over sixteen slots can be done in 63,063,000 ways. As we don't control the detailed configuration that is produced, we should be very surprised if we observe a state that can be realized in only 4,900 out of a total of 63,063,000 ways. In other words, we should expect a post-collision entropy close to Ln(63,063,000) = 18.0, and not a post-collision entropy of Ln(4,900) = 8.5.

Colliding Black Holes

Now back to black hole collisions. Does the same argument work for these?

You bet. Also for black hole collisions, to determine what is a statistically favorable collision outcome requires a comparison between alternative results. If there is an outcome that can be realized in overwhelmingly more ways than any of the alternatives, that is the outcome that will result.

Let's see how this works out. As an example we take two black holes of 3N Planck masses each. We consider two alternative scenarios:

A) 'splitting': 3N + 3N --> 4N + N + N

B) 'merging': 3N + 3N --> 6N

We don't need Einstein's general relativity, we don't need to consider curved four-dimensional spaces, and we even don't need any serious math. All we need as input is the fact that a black hole containing M Planck masses has entropy S=4πM². From this we deduce that the initial state has total entropy S=72πN², and can be realized in e^S = e^72πN2 ways.

The end products from scenario A) has exactly the same entropy as the initial state (S=72πN²) and can therefore also be realized in e^72πN2 ways. For large N, the number of realizations of this final product is spectacularly large. Even for a very modest N=5 there are e^1,800π = 10^2,456 realizations, a figure that dwarfs astronomical numbers like Googol (10¹⁰⁰). For N=20 the number of realizations is a staggering 10^39,294.

Although these are numbers beyond comprehension, scenario A) does not represent the statistically favorable transition. This is because scenario B) leads to twice the entropy S=144πN², encompassing a number of micro states that is the square of the number obtained under scenario A). For N=20 this corresponds to 10^78,588 micro states, a figure overwhelmingly larger than the corresponding figure for scenario A).

The conclusion is that although non entropy-decreasing black hole splitting reactions can be defined, these are not realizable from a statistical physics perspective.

No black hole collision will form a spray of mini black holes. Not now, not on the 21st of this month, and not in four billion years when our galaxy collides with Andromeda. Sorry to disappoint you. I'm afraid you have to place your bets on another Armageddon.