OK, that was not too difficult. As astute Scientific Blogging reader you got that right. Somalia has made the step to metric (SI) units already half a century ago, and therefore does not belong in one list together with the three remaining countries that haven't embraced the metric system yet.
The word 'yet' seems appropriate, as with 95% of the world population adhering to metric units, it seems it will just be a matter of time for the remaining tiny fraction to go metric. The more so as the 5% BUL minority (Birma, US, Liberia) is divided amongst themselves with Birma and the US each adhering to their own customary systems of units, and Liberia not having made up their mind between SI and Imperial units.
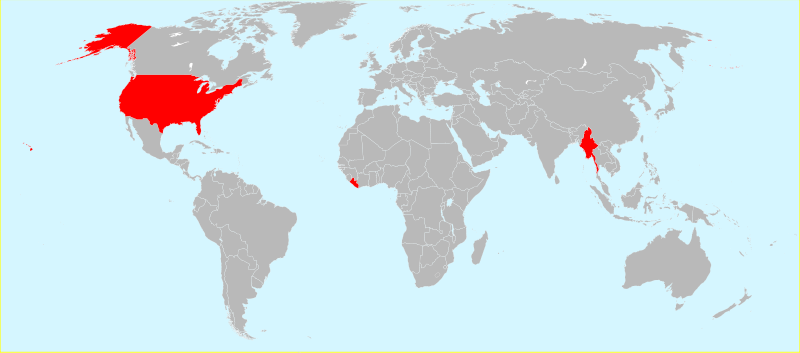
The BUL gang: the rogue nations (Birma, US, Liberia) that stubbornly refuse to accept international standards on measurements.
So give it a few years, and the world has unanimously embraced metric?
Well, don't hold your breath. Liberia will no doubt at some stage make the transition, and Burma might do the same, but the US appears to be an anti-metric stronghold. Judged solely upon the 'metrication battles' raging at internet fora, the opposition against the 'European socialist metric plot' sneaking 'commie units' into God's own country, seems deeply rooted in American society and has unmistakingly acquired distinct political and moral angles. US columnist Dave Barry clarified these sentiments in a hyperbole that might not be too far from true feelings:
"[..] my belief, as an American, is that if I have to start understanding the metric system, then the terrorists have won."
It should not come as a surprise that, to again quote Dave Berry:
"The metric system is not going to catch on in the States, unless you count the increasing popularity of the nine-millimeter bullet."
A physicist's perspective
I don't think that you will be surprised to hear that, like any physicist, I hold a strong opinion on the matter. It goes without saying that metric SI units outperform non-metric units such as the Burmese and the US units in terms of reduced ambiguity and ease of use. Anyone capable of shifting decimal points can work with metric units. Working with non-metric systems is a much more elaborate undertaking.
Let's take a simple example. How large a cube do you need to build for it to contain 1 liter? That's easy. One liter is a decimeter cubed, so a cube with sides of 1 decimeter (0.1 m) a side will do.
Now the same problem in US customary units. How large a cube should you build for it to contain a gallon?
Ehhm, that depends: do you mean a liquid gallon or a dry gallon?
Hmmm, don't see why that should matter, but let's say the cube is to contain water. I guess that should make it liquid gallons?
Right, liquid gallons it is. Let's see, if I remember correctly, 77 cubic feet equals 576 liquid gallons. So that would make one gallon equal to 77/576 cu ft. To get such a volume you need a cube with edges in feet that are equal to the third root of 77/576 which is... ehhh... got a pocket calculator?
Metric opponents often object that Burmese and US units, being based on the old British imperial system of units, are more convenient when it comes to calculations that involve division by three.* This is a nice example of the tail wagging the dog. If indeed the ease of division by three is so overwhelmingly important, one should not attempt to introduce these artificially into the measurement system, but rather work in a base six (or base twelve) numeral system, and adopt corresponding metric units. Such metric units will take shape as a senary (or duodecimal) metric system of units.
Clearly, as the world has unanimously opted for base ten rather than base six (or twelve), the ease of division by three is not all too important.
However, it is not just the calculational clumsiness of BUL units that make these inferior. More importantly, BUL units confuse matters by creating distinctions where these are not warranted (liquid volume versus dry volume), and by failing to make proper explicit distinction where such is required (pound for force versus pound for weight). The international system of units handles this much more rationally. This metric system fully recognizes dependencies between units and contains the key notion of base units from which other units are derived. For instance, volume is length cubed. Therefore, volume does not need a new unit (gallon) if one already has decided on a unit for length (foot). In SI units length is measured in meters, and volume therefore in meters cubed. Given the meter (foot) as unit for measuring length, there is no other rational choice for measuring volume than cubic meters (cubic foot).
So SI units are simply more rational than Burmese or US units. It is for this reason that no self-respecting physicist will ever utilise non-metric units.** And it doesn't matter whether she is from Birma, the US or any other part in the world.
So, should the BUL nations change over to SI?
Such a change would definitely be an improvement. However, I do not recommend this change. Yes, you read that well. I do not recommend the BUL countries to adopt metric units. Reason being that there is a much better alternative. An alternative in the form of fixing the imperial system. Overhauling imperial units to the extend that a hyper-rational system originates outperforming SI.
SI: the halfway metric system
The international system of units is broken in two aspect. Firstly, it quite arbitrarily defines the second as time unit, where a milliday (or any other decimal fraction of a day) would be more appropriate. The result is a system of units that allows derived units involving time to be non-metric. Have you ever seen a road sign indicating a maximum speed of 25 m/s? Probably not. But you will have seen traffic signs indicating values such as 90 km/h. With km/h units being used alongside m/s units, SI imports imperial-like conversion problems (with 5 m/s equating to 18 km/h) into the system.
The second aspect in which SI is broken is more subtle. To clarify the issue, we need to digress a bit.
Albert the seafarer
In a distant part of the Milky Way a nation of seafarers lives on a planet covered entirely by water. Over the course of many generations, these seafarers have perfected the art of measurement, which resulted in a system of metric units. Distance is measured in seameter (sm) and time in seaseconds (ss). Whilst they are skilled in the art of measuring horizontal distances, for a long time the word 'depth' did not enter their vocabulary. There was no such thing as 'depth' as measuring depth remained beyond their capabilities: the sea they sail simply happened to be way too deep to measure. Recently, however, the seafarers technology progressed such that by utilising acoustic echo technology they now can measure a quantity referred to as 'subsea depth. This subsea depth remains somewhat enigmatic to the seafarers as, quite naturally, they measure subsea depth as an echo time recorded in units of seaseconds.
Soon after the invention of acoustic echo technology, one clever seafarer, let's call him Albert, discovers that subsea depth is not an absolute quantity. Total depth (D) to a certain spot at the sea bottom is dependent on the position at sea, and attains a minimal value (Do) at one specific position. Albert works out a relation between both depths that involves the horizontal distance (H) between both measurement position:
D2 = Do2 + H2/c2
with the parameter c being a constant being measured in sm/ss and related to the speed of sound subsea. The discovery of this distorted Pythagorean relationship makes Albert instantly famous.
Subsequently, the seafarers make lots of efforts to measure the constant c in Albert's equation with ever increasing precision. They also successfully check c to be independent of the position at sea. The result is that c is measured to be very close to 299792458 sm/ss. A committee of wise seafarers discusses the situation, and decides that with c being a constant known to such a high precision, there is no longer the need to define the seasecond and the seameter separately. One might as well define the seameter as the distance that gives an acoustic echo in 1/299792458th of a seasecond. In doing so, c gets defined as being exactly equal to 299792458 sm/ss.
Everyone is happy with this simplification, but something keeps nagging a few seafarers. If c is defined to be a specific value, why can it not be defined to be equal to a more convenient value? Why not define c equal to unity? They discover that this can be accomplished by changing the unit of time in 1/299792458th of a seasecond. It is no coincidence that this very value happens to be the value that defines the seameter. In other words, defining c = 1 forces the seafarers to measure depth in the same unit they use for measuring horizontal distances. The choice c = 1 enforces upon the seafarers the true nature of the depth dimension: subsea depth is no different from the horizontal dimensions. The enlightened seafarers from now on no longer live in a flat world defined by the sea surface: their world has become three-dimensional, with Albert's relationship (with c = 1) simply describing the Pythagorean theorem applied to subsea distances.
Space-time seafarers
Like the seafarers in above story, we complicate things unnecessarily. Depending on the direction of measurement we use different units for measuring distance. Going from imperial-based units to metric units has not helped us simplifying things. All common units including SI fail to recognize the fact that we live in a four-dimensional world. As a result, we measure one dimension (the temporal or time dimension) differently from the other three (spatial) dimensions.
Can we elevate ourselves from the narrow perspective of three-dimensional seafarers sailing a four-dimensional sea of space-time?
Yes we can, but SI units are not the right starting point. We can achieve this goal more easily starting from imperial-based systems of units. Two key observation reveal that imperial units are much better suited to attain a relativistic perspective:
1) In a day, light happens to travel a distance very close to 1015 inches.
2) According to Einstein's E = m c2, a mass of one pound corresponds to an energy of about 1016 calories.
Based on these happy coincidences, I propose the post-imperial (PI) system of units. This system is based on the pound and the inch. The pound is the common (Avoirdupois) pound, and the inch, in PI defined as the distance traveled by light in a femto day, is about 2% larger than the common imperial inch.*** This post-imperial pound-inch system fixes both problems hampering SI units: time measurement becomes fully metric, and all four space-time dimensions are measured by the same unit.
How does this work in practice?
Space-time measurements in PI
Times and distances are measured in inches (or femtodays) a unit representing both a length and a duration. Depending on the quantity to be measured, powers of ten multiples of the inch can be used: a peta-inch equals a day, and a tera-inch is a milliday or a beat. A meeting that used to be scheduled for an hour, in post-imperial units is listed as a 40 beats meeting**** and the distance to the sun is close to 6 beats. A tick is a micro-day or giga-inch, slightly less than 0.1 seconds, or a distance twice the diameter of the earth. A marathon equals a flash or a mega-inch, and the fastest PCs operate at frequencies close to a third of a cycle per inch. Speed (spatial distance over temporal distance) works out to be a dimensionless quantity conveniently measured in nano speeds, which can be converted in mph readings simply by inflating them by 50% (with a nano speed of 90 corresponding to 60 mph).
Post imperial units do not need yards, feet, miles or any other non-metric derived units (such as parsecs or lightyears). The whole range of distances ranging from sub-atomic to astronomical is covered by decimal powers of the pinch:
Gigaday (yotta-inch): distance to Andromeda galaxy, time since start of ice ages
Megaday (zetta-inch): thickness of Milky Way, time since first Olympiad (700 BC?)
Kiloday (exa-inch): 2/3rd of distance to nearest star, life expectancy of sparrow hawk
Day (peta-inch): furthest a manmade object (Voyager 1) has travelled
Beat (milliday or tera-inch): 1/6th of the distance to the sun, one-and-a-half minute
Tick (microday or giga-inch): twice earth's diameter, fastest human reaction time
Flash (nanoday or mega-inch): 2/3rd of a marathon, cycle time for highest human audible tones
Kilo-inch (picoday): height of an eight storey building, bit lag for P-code GPS systems
Inch (femtoday): width of human thumb, cycle time for a 10 GHz processor
Milli-inch (attoday): quarter of the width of a human hair
Micro-inch (zeptoday): size of a small virus
Nano-inch (yoctoday): radius of hydrogen atom
Mass-energy measurements in PI
In the PI system, mass and energy are also measured using a common scale. This scale is based on the pound. A convenient decimal multiple of the pound, the post imperial calorie, is defined as the energy contained in 10-16 pound of matter. This makes the PI calorie about 2.5 % smaller than the common calorie.*****
As a result we can measure mass and energy ona common scale:
One micropound or ten gigacalories: energy released by burning one ton of oil
One nanopound or ten megacalories: mass of a small grain of sand, human metabolic energy consumption over a working week
One picopound or ten kilocalories: metabolic energy in one gram of fat
One femtopound or ten calories: highly energetic cosmic ray
Temperature units can be integrated into this mass energy scale by defining a post-imperial 'millidegree' as corresponding to an average molecular kinetic energy of 10^-24 calorie (10^-40 pound). As a result, room temperature is 1000 millidegree, and zero millidegree corresponds to absolute zero temperature, as it should.
Outlook
Main advantage of the PI system is that children learning the basics of PI and growing up with these units will build an intuition of space and time (and also energy and mass) being one and the same thing. Later, when they get exposed to relativity theory in science classes, math will be considerably simplified. For instance, E = m c2 simplifies into the much more insightful (and almost trivial) result E = m. The more general energy-momentum relationship E2 - c2 p2 = c4 m2 reduces to the simple Pythagorean result E2 - p2 = m2, etc. Using PI units, new generations will grow up as enlightened four-dimensional 'seafarers'.
Being a metric system based on the inch and the pound, PI provides a compromise between the gang of three and the rest of the world. Will the PI system therefore stand a chance of getting accepted?
Well, again I have to advise you not to hold your breath. And if you do, don't do it much longer than a few hundred giga-inch.
More reading
The unfortunate saga of Joseph Dombey
Notes
* Burmese units actually seem optimised for ease of division by seven.
** Most physicists employ natural units. These take the idea of SI units one step further.
*** More precisely, and in direct analogy to the definition of the meter in the international system, the inch (or femtoday) can defined as the length (or duration) of 0.794243385 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.
**** Notice that this in itself implies a 4% efficiency increase. The post-imperial world contains many of these added benefits!
***** Another distinct advantage: when adopting the PI system, your daily calorie intake can increase by 2.5% without increasing the risk of getting obese.





Comments