Do you need a dedicated yardstick for each quantifiable property?
Would the answer to this question be 'yes', then physics as we know it, would not be possible. We would not be able to relate the various properties to each other, physics laws would not exist. Fortunately, the answer to the question is a clear 'no'. We need far fewer units than one might expect based on the number of physical properties.
Consider measuring velocity. You do not need a unit of speed if you already have agreed on a yardstick for distance (a meter, a foot, a yard, a mile or whatever you agree upon) and a unit for duration (a second, a day, a heartbeat or whatever you can define as a repeatable duration). An alternative way of saying the same is: "you can build a speedometer with nothing more than a yardstick and a stopwatch".
So what is the minimum number of distinct yardsticks needed to quantify physical reality?
The widely accepted answer is 'three'. With a ruler, a stopwatch and a weighing scale you can in principle measure all elements of reality. In physics jargon, this is usually phrased as "the number of physical dimensions of reality is three". I prefer to refrain from using the term 'number of dimensions' to indicate the number of independent yardsticks, as this might suggests a link to the spatial dimensions we perceive. Just like the number of physical dimensions, the number of spatial dimensions is also widely agreed to equal three*, yet both numbers have absolutely nothing to do with each other. In fact, as we will see, the number of physical dimension we carry reflects our ignorance of physical reality more than anything else.
But there is another number of three that pops up in fundamental physics, and that number is related to the number of yardsticks. It is the number of fundamental physical constants that need yardsticks to express their magnitude. Physicists again use the term 'dimension' and refer to these as dimensionful constants. These are to be contrasted to dimensionless constants that are pure numbers such as the proton-to-electron mass ratio and the fine structure constant. The number of fundamental physical constants that are not pure numbers, but numbers dependent on the system of units used, is three. These three are: Maxwell's speed-of-light constant c, Planck's quantum constant h, and Newton's gravitational constant G. For reasons that soon will become clear, I prefer to represent these three constants in a slightly modified but equivalent way: c, h, and c4/G.
In the following it will become evident that the number of dimensionful physical constants must equal the number of independent yardsticks. This is related to the character of the ultimate theory of physics, the still elusive theory of everything (TOE). A direct consequence of this identity is that it allows the use of the fundamental dimensionful constants as natural yardsticks. This was first proposed back in 1899 by Max Planck, and the resulting natural units became known as Planck units.
Spurious units and apparent constants of nature
So our question on the required number of yardsticks is answered. But that answer triggers another question:
If we need only three units of measurement, why does the metric SI system contain as many as seven base units, and imperial systems like the US customary system even an almost uncountable number of units?
From a physics perspective, all systems of units currently en vogue are flawed, but to different degrees. When it comes to defining a system of units, the adage "less is more" is key. The fewer units, the better. The level of sophistication of a system of units is inversely proportional to the number of base units it carries.
The imperial systems - and also the metric system - contain spurious units, units that are expressible in the other units. Case in point being the American system that contains the unit 'gallon' for volume next to the unit 'foot' for length. Having the unit of foot, one does not need a separate unit for volume: with the yardstick 'foot' available, one can construct a volume of one cubic foot, and use that as yardstick for volumes.
Another way of looking at this issue is to start from the fact that 7.48051948052 gallon fit in a cubic foot. Is this number a fundamental constant of nature? A number yielding insight into the relationship between volume and length?
No, it is a manmade conversion factor. It is an exact number that can be written as 576/77 gal/ft3. Whenever an exact number is assigned to a dimensionful physical constant, you can be sure you are dealing with an artifact, a conversion factor, rather than a constant of nature that can only be known within a finite precision. Keep this observation in mind, we will encounter other such examples at deeper levels.
The metric SI system is only marginally better than the various imperial systems. Amongst its seven base units (the yardsticks for time, distance, mass, temperature, electrical current, amount of substance, and luminous intensity) several spurious units are hiding. An example being the unit for electrical current, the Ampere. Carrying the Ampere as a unit next to the units meter, second and kilogram, causes the conversion factor of 5,000,000 A2/(kg.m2/s2) to appear. Also here, the occurrence of an exact number indicates the presence of a spurious unit, in this case the unit Ampere.
A mathematical constant (2 pi) divided by the conversion factor 5,000,000 A2/(kg.m2/s2) is known as the magnetic permeability of the vacuum. Sounds pretty much like a natural constant, right? By now you should know better. Natural constants carry an uncertainty, the magnetic permeability of the vacuum does not. The vacuum permeability is a conversion factor similar to the gallon-per-cubic-foot conversion factor. A constant created by mankind, not by nature.
The same holds for Boltzmann's constant relating temperature to energy. Contrary to popular belief, Boltzmann's constant is not a natural constant, but a conversion factor. A conversion factor resulting from the introduction of the Kelvin as unit for temperature, a spurious introduction related to the failure at that time to notice that temperature is nothing more than energy per atom. Another way of saying this is that one can get rid of thermometers provided one is capable of measuring the individual energies of large collections of atoms.
Extending this critical review of SI base units, one can derive that a total of four out of the seven base units are spurious. In SI, all that is needed to measure reality, are the three units 'kilogram', 'meter' and 'second'. As remarked earlier, there are only three physical dimension.
Yet, something is not right. In the SI system, the meter is operationally defined in terms of the second using the speed of light c as conversion factor. But this conversion factor is defined as exactly 299,792,458 meters per second. And we just argued that any presence of an exact dimensional constant indicates a spurious unit.
What is happening here? Is the speed of light a fundamental constant of nature, or is it a manmade conversion factor? And as the speed of light is defined with zero uncertainty, does it mean we have a spurious unit of measurement hidden amongst the three fundamental units?
We need to delve a bit deeper into fundamental physics. Starting from Newtonian mechanics, we will explore the route that brings us via special and general relativity to quantum gravity (the 'theory of everything'). The tool that we will be using is dimensional analysis. So, rather than attempting to represent the full theories, we will zoom in on the 'yardsticks' required to describe the features of the progressively more general theories. The outcomes of this exercise will probably surprise you.
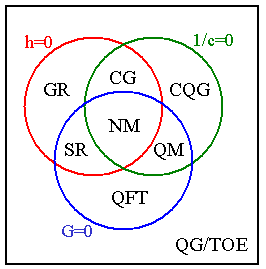
Centuries of physics condensed in a single Venn diagram. The various theories are grouped according to which aspects of reality are ignored. Red circle (h = 0): theories ignoring quantum effects, blue circle (G = 0): theories ignoring gravity, green circle (1/c = 0): theories ignoring relativistic effects. Specific theories are labelled NM: Newtonian mechanics, SR: special relativity, QM: quantum mechanics (non-relativistic), CG: Newton-Cartan gravity, GR: general relativity, QFT: quantum field theory, CQG: Cartan quantum gravity, QG/TOE: quantum gravity also known as theory of everything.
From Newton to Einstein
At the end of the 19th century, when the reality of atoms and molecules did sink in, it became apparent that a physical reality of atoms and molecules behaving according to Newton's laws, should need no more than four different yardsticks:
Newtonian Reality <--- Energy + Momentum + Distance + DurationDistance and duration (or space and time) is 'the stage' on which all of Newtonian dynamics takes place. Momentum changes in accordance to Newton's second law, and energy provides the link between momentum and velocity, thereby allowing the momentum changes to be linked to movements relative to 'the stage'.
In the above, energy could be replaced by mass, and momentum could be replaced by velocity, etc. This is not relevant. What is relevant is that a Newtonian description seems to require four physical quantities. However, as we have already seen, these four quantities can not be independent, as the number of independent yardsticks is limited to three. Apparently the above Newtonian perspective gives a too rich description of physical reality.
This was the situation that Albert Einstein faced in 1905. His view on physical reality dramatically reduced the number of physical units required. In a stroke of genius he reduced the number of physical dimensions, not by one, but by two. He did so by clarifying that distance and duration are two manifestations of one-and-the-same thing.** For lack of a better term I will refer to this more fundamental physical dimension as 'SpaceTimeExtent'. Interestingly, in order to combine distance and duration into one physical dimension, Einstein also had to combine energy and momentum into a single more general concept, which I will refer to as 'SpacetimeContent':
(Distance)2 ---> (c) * SpaceTimeExtentThe result of this transformation is a special relativity description of physical reality that contains only two physical dimensions:
(Duration)2 ---> (1/c) * SpaceTimeExtent
(Energy)2 ---> (c) * SpaceTimeContent
(Momentum)2 ---> (1/c) * SpaceTimeContent
Special Relativistic Reality <--- SpaceTimeContent + SpaceTimeExtentThe quantity 'SpaceTimeExtent' is effectively a space-time area (in SI measured in units of meters times seconds), and 'SpaceTimeContent' is the product of energy and momentum (one might say: an area in energy-momentum space). Both quantities are more fundamental than the four Newtonian concepts of distance, duration, energy and momentum. The quantity SpaceTimeExtent measures the square of the separation between two events in space-time. In a later post I will elaborate on SpaceTimeExtent as a means to understand Special Relativity without being burdened by any math.
We haven't discussed yet the constant c used in the above transformation from Newtonian to Relativistic reality. As you probably have guessed: it is the same c that we encountered above, the constant known as 'the speed of light', relating 299,792,458 meters to a second.
As long as we work with the more fundamental concepts SpaceTimeContent and SpaceTimeExtent, we do not need this constant c. Progressive insight (describing reality using the more fundamental concepts SpaceTimeContent and SpaceTimeExtent) has effectively made this constant disappear. This gives us a clear answer to the question "is the speed-of-light a fundamental constant or not?" Obviously, if it were a fundamental constant, it would not have been possible to make it disappear from theory. The speed-of-light is a manmade conversion factor that doesn't raise its ugly head, unless we decompose SpaceTimeExtent into the less fundamental but more familiar variables distance or duration, and only so if we use an awkward system of units. A system containing incompatible units for time and distance.
In essence, Einstein managed to demote the speed of light from it's status as a fundamental physical constant, into a mere conversion factor equal to 299,792,458 m/s. A conversion factor not in any way more fundamental than the volume-to-length conversion factor 7.48051948052 gal/ft3.
Note that before Einstein we required three yardsticks (in the metric system the units kg, m and s) as well as three fundamental constants: c, h and c4/G. When Einstein completed his special theory of relativity, we were left with only two yardsticks (in the metric system: m*s and kg2*m3/s3) and two fundamental constants: h and c4/G.
But Einstein wasn't finished yet.
Einstein strikes again
Einstein worked ten more year, and in 1915 presented his general theory of relativity. A magnificent generalization of his earlier theory of relativity. A generalization that allowed him to include the effects of gravity. And again, Einstein managed to reduce the number of yardsticks required. This time, he did so by clarifying that SpaceTimeContent and SpaceTimeExtent are two manifestations of one-and-the-same thing.*** the 'thing' is known as the action, or more specifically, the Einstein-Hilbert action:
SpacetimeExtent ---> (G/c4) * ActionThe result of this transformation is a description of physical reality that contains only one physical dimension:
SpacetimeContent ---> (c4/G) * Action
General Relativistic Reality <--- ActionWith this result, Einstein eliminated SpaceTimeExtent from the description of physical reality. Thereby demonstrating there is no room and no need for a stage on which the physics takes place. The stage got replaced by something more fundamental, the action, the play itself.
The constant c4/G appearing in the transformation from SpacetimeExtent and SpacetimeContent into Action, is a force constant associated with gravity. It represents the self-gravitational force generated when space-time is deformed to its maximum. This maximum is reached when a black hole horizon shields further curvature from our observation. Also this force constant is no more than a conversion factor. A conversion factor that pops up when working in terms of physical properties less fundamental than the Einstein-Hilbert action.
All-in-all, Einstein reduced the number of independent yardsticks from three to two and finally to one. The only remaining yardstick being the one that measures the action, in SI represented as the unit kg*m2/s. The number of dimensionfull physical constants got similarly reduced from three to two and finally to one. The only remaining constant being Planck's constant h, measured with the same yardstick as the action.
It seems physical reality got reduced to one yardstick and one fundamental constant. But we are not done yet, as I haven't told you about an amazing path of research that ran partly in parallel to Einstein's efforts: quantum physics.
From Einstein to Feynman
Einstein was instrumental in realizing the advent of quantum physics, but turned his back to this theory when he felt its philosophical consequences were getting too weird. Others continued, and eventually a younger generation including brilliant physicists such as Richard Feynman took over. As a result of these efforts, quantum physics became what is without doubt the most successful theoretical framework ever constructed in physics. A success that left Einstein sidelined in his later life.
Some profound new insights resulting from quantum theory is that one can not associate one single number to the concept 'action'. This is directly related to Werner Heisenberg's uncertainty relations that stipulates products such as distance times momentum, and duration times energy, can be determined no more precisely than roughly within Planck's constant h.
It was Richard Feynman who in 1948 showed how to represent the concept 'action' into a form compatible with the principles of quantum physics. Effectively, to describe a system quantum-mechanically, the action expressed in units of Planck's constant gets associated with a sum over all alternatives such that constructive and destructive interference takes place between the alternatives summed over:
Action/h ---> SumOverAlternativesThe precise way in which Feynman sums are constructed is beyond the scope of this post.**** What is relevant, though, is that this Feynman sum approach yielded highly successful theories known collectively under the name Quantum Field Theory (QFT). QFT describes the whole physical reality except for gravitational phenomena. In particular, all of modern particle physics is based on QFT. It is no exaggeration to state that QFT is the most strictly tested theory of nature.
The Final Frontier
Congratulations, now that you have digested all the above, it should be obvious how to derive the ultimate physics theory, the long-awaited Theory Of Everything (TOE). We take Feynman's SumOverAlternatives approach, and apply it to the action in Einstein's general theory of relativity.
With the Einstein-Hilbert action divided by Planck's constant replaced by a Feynman sum, the result will be a description of physical reality based on one single dimensionless quantity:
TOE Reality <--- SumOverAlternativesA description of physical reality that requires no physical units at all. A physical reality that reduces the whole universe to mere counting. Why has no-one thought about this?
Well, fact is that countless numbers of physicists tried exactly this. Feynman was one of them. Each attempt, however, result into disappointment. No matter how the Feynman sum for the general relativistic action is constructed, when evaluated it invariably adds up to infinity. Generations of physicists have tried to tame the divergences in the theoretical description, but no-one succeeded in preventing meaningless infinities popping up.
Does this mean a TOE does not exist?
Not at all. The conviction that a TOE can be constructed might seem wishful thinking, but there are reasons to believe that a divergence-free TOE exists but requires a profound rethinking of the fundamental concepts of physics. A potential solution could be realized by finding a way to transform the Einstein-Hilbert action into a holographic description, and to apply the Feynman sum approach not to the Einstein-Hilbert action, but to the corresponding holographic action. The hope is that the vastly reduced number of paths in the holographic Feynman sum would tame the divergences.
Here I can not go into any depth into these issues. Rather, I want to conclude with some thoughts on what a TOE would realize in terms of its description of physical reality. As should be clear from the above, a TOE will describe the whole physical universe in terms of one single dimensionless quantity, the Feynman sum. All of physics will in essence be reduced to counting rather than measuring. Dimensionful physical constants will be absent from this theory. TOE will be a theory written in pure numbers that don't require any yardsticks.
The character of the TOE will be that of a probabilistic theory. The sum over all alternatives will yield a result that need not be a positive number. The square of the absolute value of this number will be the probability assigned to the predicted outcome. The TOE will predict the large scale features of the universe such as the cosmic acceleration likely within a narrow uncertainty range. But a vast majority of small-scale detailed outcomes such as coin flips will be predicted with 50/50 probabilities. The TOE will not be a magic crystal ball.
Is this disappointing? Not at all. As James Hartle has stressed: this is a hopeful message for all working on the construction of the TOE. It is only because so little of the complexity of the present universe will be predicted by the TOE, that we stand a chance to discover it.
The real value of a TOE will stretch far beyond it's predictions. It is the identification of the true elements of reality, the unification of all of physical reality into one single concept that will yield the TOE its value. Less is more, particularly when it comes to understanding nature.
Notes
* Yes, I know: modern physics makes us doubt even this very fact, hence the phrasing "widely agreed to equal three". Given that both numbers are unrelated, all conclusions from this blogpost hold regardless the exact number of spatial dimensions.
** Einstein actually did not achieve this on his own. Einstein was gifted with a brilliant physical intuition, but was less than brilliant when it came to casting his intuition into the most general and most elegant mathematical format. It was the mathematician Hermann Minkowski who, in 1907 formulated Einstein's ideas in terms of a four dimensional space-time.
*** Again, Einstein needed help from a mathematician to formulate his theory into an elegant form. This time it was David Hilbert who showed Einstein the way.
**** if things go as planned, the next Hammock Physicist post will be a special guest post written by an extraordinary guest. In this guest post you will be presented a beautiful and simple example of a Feynman sum. Watch this space...





Comments