It is easy to marvel at Einstein's relativity theory. It is less easy to really understand relativity. At least so it seems. Understanding relativity requires abilities in predicting with confidence the outcomes of relativistic experiments. For that you need a PhD in physics. Right?

I believe this to be a too pessimistic thought. Special relativity forces you to abandon some deep-rooted concepts about time and simultaneity, yet once you have accepted this, Einstein's theory is remarkably simple and elegant. In a recent blog entry, I made the case that the essence of relativity can be captured in the form of a simple graphic display: the mass-energy-momentum triangle. I demonstrated that this simple Pythagorean construct captures a variety of relativistic notions, such as mass being equal to rest energy, the speed of light setting a limit to the speeds attainable by massive particles, and light having momentum despite the absence of mass.

But that is all conceptual stuff. You might be tempted to brush all of it aside as theoretical blah blah. Stuff that doesn't tell you how to predict the outcome of a relativistic experiments. Although you have read about mass-energy-momentum triangles, you still have no clue how to predict the outcome of, say, a relativistic collision.

But hold on. Let me demonstrate that mass-energy-momentum triangles can be used to operationalize relativity theory. We are going to draw some triangles that will predict the outcome of relativistic collisions.

Sticky collisions
Let's consider two sticky objects of equal mass. One of these gets accelerated to relativistic speed, and collides at 15/17^th of the speed of light on the other object that is at rest. Due to their stickiness, both objects get glued together in the collision. At what speed will the resulting composite object travel?

This is by no means an easy calculation. As we will see, a lot happens: momentum gets transferred, energy gets converted, masses change, etc. And all of this at breakneck speeds close to the speed of light at which Newton's laws of mechanics are no longer valid. Yet, this collision problem is easy to solve provided one is able to draw the relevant mass-energy-momentum triangles.

Do you recall the mass-energy-momentum triangle for a particle traveling at speed v and with total energy E? This is a right-angled triangle with hypotenuse of length E, and one edge represented by an arrow of length E v/c (see figure), with c representing the speed of light.


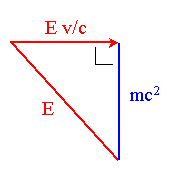
The mass-energy-momentum triangle that summarizes Einstein's special relativity theory. The total energy E, momentum E v/c (or more precisely c times momentum), and rest energy mc2 form a right triangle. The red edges represent conserved quantities, with momentum possessing a direction and being represented by an arrow. The blue edge, whilst not conserved, is independent of the frame of reference chosen.

Let's apply this construction to the collision as described in the problem. We have two particles entering the collision, and one particle emerging from the collision. So we need two triangles to describe the pre-collision configuration, and one triangle to describe the post-collision configuration. The state prior to the collision involves a particle moving at v/c = 15/17 towards a particle at rest (v/c = 0). It immediately follows that we have one right triangle with hypotenuse 17 and edge 15, and a degenerate right triangle with edge of zero length. These triangles being right angled dictates the length of the unknown edges. Using the Pythagorean theorem, it follows that the pre-collision triangles have sides 17:15:8 and 8:0:8.


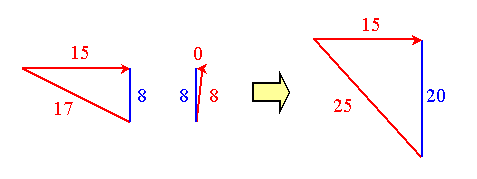
Sticky collision represented in mass-energy-momentum triangles.

Energy and momentum conservation now define the final state. The total energy prior to the collision is represented by the two hypotenuses: 17 + 8 = 25. The total momentum is represented by the two edge arrows: 15 + 0 = 15. So the final state we can represent by a triangle with hypotenuse 25 and momentum arrow 15. To render this triangle rectangular, according to Pythagoras the mass edge needs to have length 20. The resulting triangle is shown at the right-hand side of above figure. We conclude that the composite particle emerging from the collision moves with speed 15/25 = 3/5 times the speed of light.

That was easy, isn't it? By drawing just three right triangles, and using energy and momentum conservation, the answer to the question followed without the need for any tedious math. One thing is worth noticing: whilst energy and momentum are both conserved in the collision, mass (or rest-energy) isn't. The rest-energy prior to the collision is 8 + 8 = 16, whilst after the collision it is 20. A gain in rest-energy has occurred. There is nothing wrong with this: whilst the total energy is conserved, this does not hold for the various forms of energy. Effectively what happened is that the collision caused some of the kinetic energy being transferred into rest energy. I will come back to this point later.

Another perspective
The beauty of relativity theory is that the same outcomes for physics experiments can be predicted from any perspective. For instance, we can investigate the same sticky collision from the perspective of an observer co-moving with the center-of-mass.

Such an alternative perspective changes the lengths of the energy and momentum edges in the various triangles, but leaves all the rest-energy (mass) edges untouched. It follows that the center-of-mass state prior to the collision is described by two mirror-image right triangles with rest-energy edges of length 8, and momentum edges with equal (as of yet unknown) lengths but oriented in opposing directions. The final state is characterized by a momentum edge that is the vector sum of both pre-collision momenta and therefore has length zero. So we have a degenerate final-state triangle with rest-energy edge equal to that observed before (20). The final-state energy edge must have the same length, and total energy conversion now tells us the the pre-collision center-of-mass triangles must have hypotenuses of length 10. The Pythagorean theorem completes the center-of-mass description by prescribing pre-collision momentum edges of length 6.


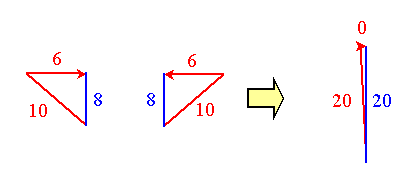
The same sticky collision from a center-of-mass perspective. All triangles change in shape, but the rest-energy (mass) edges remain unchanged.

Relativistic velocity addition
Both descriptions of the collision are equally valid and fully consistent. These represent the same physics from two different perspectives. This is the essence of relativity theory. However, if you have paid close attention, you must have witnessed a strange thing happening. In the center-of-mass description we observe two particles colliding head on, each with speed 6/10 = 3/5 times the speed of light. In the original description, we observed the collision from the perspective of one of the two particles, and saw the other particle approaching at 15/17 times the speed of light. According to our triangle-based model, two times a speed of 3/5 c equals a speed of 15/17 c. This is at odds with what one would expect based on Galilean velocity addition. But it is exactly in line with Einstein's predictions.

Evidently, the full relativistic velocity-addition formula is contained within the same simple triangle that captures mass-energy equivalence. All you need to know about Einstein's special relativity theory is summarized in a simple annotated triangle. Can you imagine that some physicists claim special relativity theory is in essence simpler than Newtons laws?

From triangles to atom bombs
I promised you to come back to the mass gain observed between the initial and final state of the collision. Can we observe such a mass gain when we throw two sticky balls against each other? Not really. The fact is that you would need a very, very special glue to ensure both balls stick together when you smash them towards each other at speeds close to the speed of light. Such glue you won't find at your local Walmart.

But we can observe the reverse process: a ball splitting in halves, thereby losing mass and propelling the ball fragments to relativistic speeds. Such balls with the capability to transfer significant portions of its rest energy into kinetic energy have had a profound impact on the recent world history and continue to cause deep conflicts. This despite the fact that virtually all sovereign countries in the world have signed an agreement to refrain from putting large masses of such balls together.

As you might have guessed, these balls are tiny. Considerably smaller than atoms. And the glue that keeps them together is truly spectacular. Break that glue and you become Dead, the Shatterer of Worlds.