In posting my answers, which are of course as cryptic to outsiders as are the questions themselves, I will try to provide some additional explanation for the non-experimental particle physicists among you; experts are instead advised to skip altogether the text in italics which follows each answer, lest they find something incorrect -I usually sacrifice some accuracy for clarity when I explain things to non-insiders.
The selection of which questions to pick has been made arbitrarily -part of it was driven by my lazyness in using latex, which drove me to skip answers with too many formulas. You can however request specific answers to the questions left over if you so desire, and I will try to provide them.
Q 1.5: An electron with medium-high energy releases in a BGO block energy which generates a signal of about 10^6 electrons per GeV, and in a block of lead glass of the same dimensions a signal of about 10^3 electrons per GeV. What is the reason for this difference ?
A 1.5: Bismuth germanate (BGO) is a scintillating material, and relativistic charged particles release blue light (
In lead glass, which does not yield scintillating light, photons are instead released by Cherenkov effect. One typically obtains
E 1.5: Scintillation is a phenomenon occurring in many materials, when a fast-moving charged particle traverses them. It consists in the production of light by atomic electrons which get excited by the crossing charge and then release the energy by yielding blue or ultravioled photons. Typically a scintillating material which is transparent to its own generated light can be coupled to a photomultiplier tube, a device which has an optical window accepting the light quanta. Photons release electrons when they hit a photocathode, by means of the photoelectric effect (alkali materials have one outer electron which is easy to kick off the atom). The electron is then accelerated in a strong electric field inside the tube, which multiplies the yield. Finally the electrons are collected and release an electric pulse.
Cherenkov light emission is instead a different phenomenon, which arises when a charged particle travels in a medium with a speed faster than that of light (light speed in a medium of refractive index n is c/n). It is a sort of "shock wave" generated by the fast-moving particle, and it consists in bluish light. The Cherenkov angle
Q 1.6: In a given e.m. calorimeter the statistical contribution to resolution is
A 1.6: No, since besides the resolution due to the statistical fluctuations of the detected signal, which for a 50 GeV electron entirely absorbed equals 0.07/7.1=0.01, there are constant contributions (
E 1.6: A high-energy electron hitting a dense medium generates additional electrons by two coupled processes, bremsstrahlung and production of electron-positron pairs. Bremsstrahlung occurs when the electron's velocity is affected by traveling in the strong electric field of a high-Z atom, and consists in the radiation of an energetic photon. The photon can then yield electron-positron pairs if its energy is sufficiently large, as it iself interacts with the heavy nuclei of the material. The process results in a multiplication of the number of electrons, and the number of produced electrons is a linear function of the incident energy. From the proportionality between N and E a calibration allows to measure E from N; N fluctuates according to Poisson statistics, so its uncertainty is
Q 1.8: A cube of NaI(TI) scintillator read out by a photomultiplier tube measures the line of cesium; estimate the resolution in energy, listing the factors that contribute.
A 1.8: The principal line of cesium has an energy E=0.662 MeV. The efficiency of a scintillator NaI(TI) is of 13%, so that the luminous energy released equals 86 keV. If the average energy of released photons is of 3 eV, there are about 29,000 of them per decay. This signal is sufficient to guarantee a small stochastic contribution to energy resolution. The latter is dominated by constant contributions (noise) and non-linearity in the crystal output.
E 1.8: Similarly to what is explained in E 1.6 above, the fluctuation in the expected number of secondary photons produced in the scintillation process follows Poisson statistics and is thus
Q 1.9: In a measurement where a threshold
A 1.9: If the rise time is of 10 ns and the signal equals 1 Volt, the threshold fires after 4 ns, while for a 0.5 V signal the threshold only fires after 8 ns. There is thus a uncertainty of 4 ns on signal arrival time. A differentiation of the signal may reduce this uncertainty.
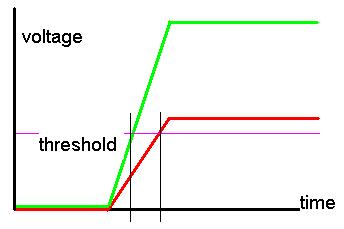
E 1.9: The figure shows visually what is explained above: if the electronics responds to a signal by raising a voltage as shown, the non-instantaneous rise time does affect the time resolution, if the plateau voltages change. The green voltage curve is quicker to go above threshold than the red one, and this causes signals of different strengths to trigger at different times.
Q 2.1: Compute the average number of interactions per bunch crossing for a luminosity L=2.5E31 cm-2 s-1, if the total cross section is sigma=20mb and bunch crossings occur every T=4 us. What is the probability of having zero interactions in a bunch crossing ?
A 2.1: The rate at 2.5E31 is
E 2.1: Luminosity is a parameter of a particle collider. It is a product of the particles in each beam intersecting per second in the collision point. The smaller the area where the beams intersect, the larger the luminosity, for a given number of particles. The master formula which connects luminosity to the rate of collisions of any given kind is
Q 2.5: An experiment with continuous beam is endowed with a trigger with efficiency 20%. The natural frequency of events to be selected by the trigger is f=5 kHz. The acquisition system generates a dead time T=1 ms per every collected event; during dead time the trigger and detector are ineffective. Determine the average frequency of data collection.
A 2.5: If the trigger efficiency to accept data is 20% the input rate is 5kHzx0.2=1 kHz, or on average one event every T=1 ms. Each accept generates a dead time of 1 ms, following which a new event is collected on average every T seconds, since the average time needed to get another accept is the integral from zero to infinity of the Poisson distribution of average t/1ms evaluated at N=0, or
E 2.5: The trigger system of a particle physics experiment is a software or hardware device capable of reading out the detector and determining whether some conditions have been met. If the answer is positive, the trigger "fires" and the detector is readout; otherwise, the event is discarded. This allows experiments to run high rates of collisions, collecting only the most interesting and rare ones, still at a manageable rate. In the exercise some trivial calculations are made to determine what rate can be acquired, if the system becomes temporarily inactive every time an event is collected (dead time).
Q 2.7: To monitor the luminosity of a collider two scintillation counters A and B are used, which are located before and after the interaction region. The packets cross every
A 2.7: Let us call A,B,C the average frequency of signals for each beam crossing in counters A,B and their coincidence. One has A=0.753, B=0.667, C=0.543. If D is the average frequency of true coincidences in C due to the presence of a real event, one may write the average counting frequencies in A and B not due to real events as
and the frequency of C coincidences really due to real events as
where the last factor (1-D) accounts for the fraction of crossing between the bunches when casual coincidences may occur. One thus finds for D the expression
With the data in the question, one finds D=0.331,
E 2.7: This question is a classic example of how the computation of coincidences among different counters is affected by the rate of fake rates. The setup is meant to determine the rate of real coincidences due to beam crossings that produced an interaction: the interaction causes particles to be emitted in all directions, firing the counters A and B; the rate of firing of A and B not due to interactions has to be accounted for, as described by the formulas above.
Q 2.9: A spectrometer for particles with unit charge and momentum of few GeV/c is made by three parallel planes of position detectors with a resolution dx=100 um, distanced a=20 cm and immersed in a uniform magnetic field B=1 T, parallel to the detector planes and orthogonal to the measured coordinate. Particles incide almost perpendicularly to the detector planes. Estimate the transverse momentum resolution at p=2 GeV/c.
A 2.9: For particles of unit charge and momentum p the curvature radius is
R=p/0.3B = 2/0.3 = 6.67 m and the angle theta in the figure below is
For simplicity, let us consider the situation where the particle hits the first layer with an angle of incidence equal to the exit angle out of the third layer, as in the figure below.
Under such conditions, if one measures the difference of position between the hit in the second layer and the hits in the first and third layers, one finds
and the error on delta x is equal to
Delta x can be expressed by R and the angle theta as
Since
E 2.9: Charged particles moving in a magnetic field experience what is called Lorentz force, a force that acts orthogonally to the direction of the velocity, causing the trajectories to follow curved paths. From the curvature, the momentum can be deduced by the simple formula p=0.3 BR, which results from equating Lorentz and centripetal forces. The curvature can be determined if one measures at least three points of the trajectory; uncertainty in the position of the points results in uncertainty in the determined momentum.
Q 3.1: An experiment selects signal events with a frequency f and events of background with a frequency b. Calculate the data taking time necessary to observe the signal with a statistical significance of n sigma.
A 3.1: To observe a signal with significance of n standard deviations (only due to statistics), one needs a data taking time t such that
One must thus have
E 3.1: If a signal has frequency f, the number of events that are collected is obtained by multiplying f by the collection time t; the same can be said for background events. One can attribute to the signal a statistical significance if one imagines to perform a counting experiment: if one expects only background at a rate b, after a time t one will observes an excess, whose significance is the number of signal events divided by its uncertainty. The uncertainty is given by the fluctuation in the number of collected background events. The latter equals the square root of the collected background, hence the formulas above.
Q 4.6: Consider the decays
A 4.6: As can be seen by the schematic diagram below, the two amplitudes are related by the ratio
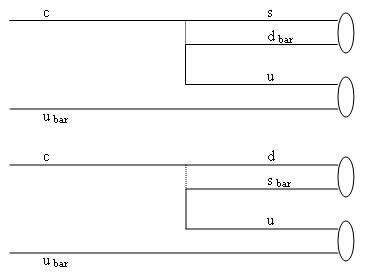
E 4.6: Weak interactions change the flavor of quarks by the emission of "charged current" weak bosons. These W bosons are very massive, so the probability of their virtual emission by the much lighter quarks involved in reactions such as the ones pictured on the left is very small -hence the slowness of the reaction, and the "weakness" of the interaction.
In the picture time flows from left to right. The top diagram shows a D0 (c ubar) decay into the anti-K0 (s-dbar) pi0 (u-ubar) final state, the bottom diagram shows the other considered decay (c-ubar going into a d-sbar plus u-ubar state). The line connecting the top quark line and the second line from top represents the propagation of the exchanged W boson. At each ends of the W propagation line, the top diagram has a charm quark turning into a strange one, and a u and d quark; the bottom diagram instead sees the connection between a charm and a down quark, and between a up and a strange quark.
In addition to the general weakness of weak interactions, whenever a quark changes into another, there is a "vertex factor" to account, equal to the element of the Cabibbo-Kobayashi-Maskawa (CKM) quark mixing matrix, denoted as
Q 4.8: What is the value to first order of the ratio
A 4.8: The ratio R is equal to three times the sum of squares of quark charges, where only quarks contributing to final states have to be counted. At 6 GeV the four lightest quarks contribute, so R=10/3. For the branching ratio BR of W bosons into leptons one has the value 1/9 for each lepton species, since the possible final states are
E 4.8: When an electron and a positron collide at high energy, they annihilate into a virtual photon which has a large energy (twice the energy of the beam, for a symmetric machine). The photon then "converts" into a pair of charged fermions -quarks or leptons- in a democratic way: each fermion pair gets an equal share, after accounting for the proper "coupling" of the fermions to the photon -basically, the electric charge they carry, which has to be squared in the formula. From this one derives the ratio R between the number of quarks and muons that are produced. This ratio is very important since it is a direct probe into the number of quarks which exist below a certain mass (the photon energy has to be larger than twice the mass of the fermion, to produce it).
A different argument, still involving fermionic democracy (or, for HEP physicists, universality), determines the different branching fractions of W bosons into quarks or leptons. The color of quarks has to be accounted when computing the different shares of branching fractions or productions.
Q 4.13: What is the ratio between
A 4.13: The ratio of branching fractions depends on the coupling of the Higgs boson to b-quarks and tau leptons, and is thus proportional to the square of fermion masses. There is then a factor 3 to account for the colour of quarks. At 120 GeV the b-quark mass (which runs with the energy at which it is probed) is roughly double as that of the tau lepton (which does not run), so one can estimate a ratio equal to
E 4.13: Higgs bosons can decay to any particle-antiparticle pair if these have a non-null mass: in fact, the Higgs "couples" to elementary particles with a strength proportional to the square of the mass of the particles. When computing the possible decays, one must account for the relative strength of the couplings, as much as the different kinds of particles that may be produced -if we cannot distinguish them. That is the case of bottom quarks: since the colour of quarks is a unobservable characteristics, we must add the contribution of the three colours when we compute the branching fraction to quarks. The other subtlety in the problem is due to the fact that b-quarks have a "rest" mass of 4.2 GeV, but when one considers these particles in high-energy interactions, their effective mass is smaller: this is due to the fact that strong interactions become less strong as energy increases, and the quark mass is affected by this variation.
Q 4.17: A photon may convert into an electron-positron pair next to an electron rather than next to a nucleus. In such case, what is the threshold energy ?
A 4.17: The minimum energy of the process can be obtained when the three final electrons are at rest in the center-of-mass system, in which case energy conservation gives
from which follows immediately
E 4.17: The process called "photon conversion" consists in the materialization of a pair of charged fermions (electron-positron pairs are the most likely, due to the fact that the electron is the lightest charged fermion) by the quantum of light. The photon cannot convert into a pair in vacuum, however, because the process would violate the conservation of energy-momentum: there needs to be a matter field where the conversion takes place, capable of absorbing the excess momentum. These concepts are hard to explain and digest if one does not run the actual computations of relativistic kinematics on a piece of paper. In any case, the question entails a simple calculation of energy conservation.





Comments