The reason why CDF took it easy is that at the Tevatron this is really not the most sensitive way to search for a standard model Higgs boson: the Higgs decay to a pair of photons is predicted to be quite rare -only one in a thousand or so; and the Tevatron, however a lucky place for particle physics, is not an efficient factory of Higgs bosons. So rarity is a real hindrance in this case.
Rudiments of the Higgs decay to photon pairs
Rather than why the Higgs decays so infrequently to photon pairs, one would be more justified to ask why it decays that way at all. In fact, the Higgs particle interacts with other elementary bodies in measure proportional to the mass of these; thus the photon, having zero mass, cannot have any business with the Higgs! The argument can even be turned around: photons interact with elementary particles only by virtue of the electric charge those possess: and the Higgs boson is neutral, so there can be no direct coupling among them.
The key word here is "direct". In fact, the way the Higgs boson can indeed disintegrate in a double flash of energetic light quanta is via an indirect quantum process. It is quite instructive to examine it, so let me do it here very briefly.
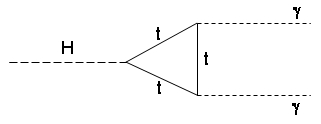Since the Higgs couples more readily to massive particles, let us take the top quark, the most massive of them all. One may imagine that the Higgs emits a top-antitop pair, and the latter pairinstead of leaving the crime scene lingers around, and produces a virtual loop. This loop is bound to radiate out again the energy it borrowed from the energy of its originating Higgs boson: and it can do so by emitting a pair of photons! This is what is described by the Feynman diagram on the right.
Of course, the process whereby a top quark radiate a photon is governed by the rules of quantum electrodynamics. In particular, each "top-photon" vertex has a probability of occurring which depends on the "fine structure" constant,
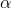. So the double photon emission must be proportional to 
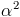, a small number (1/137^2 = 0.000053).Now take instead the quantum-chromodynamical radiation of a pair of gluons from the top quark loop: this is governed by very similar physics considerations, and -except from some proportionality constant- the only difference with photon pair emission is that now we must use
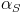, the strong coupling constant. Aha!Since
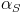is more than one order of magnitude larger than alpha, one expects that the decay 
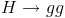be over two orders of magnitude more frequent than the beautiful 
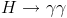one. Beware, here I am ignoring color factors -which increase the difference-, as well as the fact that the decay to photon pairs may occur also thanks to a loop of W bosons -which does not contribute gluon pairs, and favors photons. The estimate we made is rough, but it suffices to demonstrate that the decay to diphotons is rare. In fact, even the one to gluon pairs is not one of the principal decay modes of the Higgs boson, regardless of its mass.The different branching fraction of the Higgs boson to gluon pairs and photon pairs can be checked on the graph below, which shows how the two have a quite similar behaviour as a function of the unknown mass of the Higgs boson: the probability peaks at about 120 GeV, to then decreases rapidly because of the strong competition from the direct decay of the Higgs to W boson pairs, which at high mass becomes the most frequent mode of disintegration.
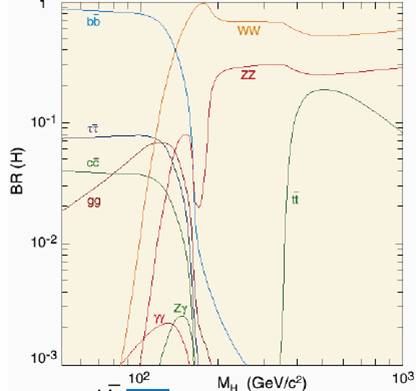
The red "bump" at the bottom left is the one describing the probability of a decay to diphotons; the brown one sitting 30 times above is the one sizing up the branching ratio to gluon pairs.
Once we have sized up the Higgs branching ratio of interest, we can more meanginfully go back to computing how many decays to photon pairs one might expect CDF to collect in its 5-femtobarn dataset: the one-in-a-thousand branching fraction is understood.
The calculation is easy to do on the back of an envelope: with five inverse femtobarns of collisions, and with a total Higgs boson cross section of one picobarn (=1000 femtobarns), one expects to have produced of the order of
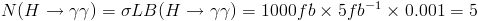such decays. Five is a nice number, but it is small if compared to the large number of events yielding photon pairs from sources totally unrelated to Higgs boson production. And it becomes even smaller when one considers that the detector efficiency to correctly identify a energetic photon is smaller than 100%.
On the plus side, CDF is endowed with a surprisingly good electromagnetic calorimeter. One of its "wedges" -the 48 15-degree azimuthal pieces making up the central part- is shown in the picture; note the alternating horizontal layers of lead sheets and scintillating plastic material. The oblique segmentation in "towers" allows to read out and distinguish the signal of particles emitted at different angles with respect to the beam. The surprise doubles if you consider that this detector was built in the early eighties -over 25 years ago!! Now, admittedly the progress in electromagnetic calorimetry in these 25 years has not been overwhelming; and yet, the excellent resolution for a Higgs decay to two photons that CDF may boast in the figure below is indeed quite pleasing: 2.4% !
The histogram above is obtained by a Monte Carlo simulation of Higgs decays to photon pairs. CDF can claim that the prediction is correct based on the extreme care with which the simulation is tuned on experimental data: and not just proton-antiproton collisions but critically, test-beam results performed a long time ago!
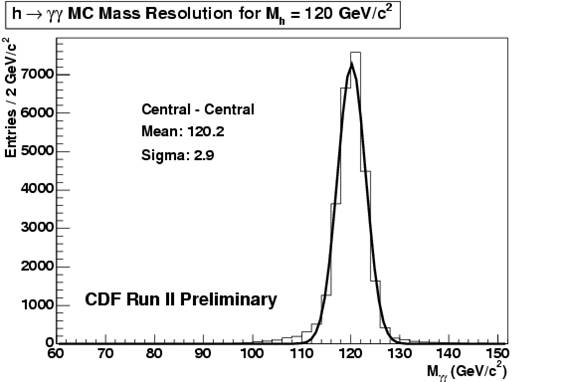
To compare the CDF resolution on photon pairs with something which is "state-of-the-art", let us take the one expected by the CMS detector, which may legitimately boast about its homogeneous bars of lead tungstate, a material very difficult to produce and extremely costly. The projected resolution for a Higgs decay to diphotons in CMS can be deduced from the signal shown on the right, which CMS may see with 100 inverse femtobarns of proton-proton collisions. It is quite nice to see how the Higgs signal will stand out from backgrounds; but the resolution is not overwhelmingly better than that of good old CDF! Twice better, perhaps.A couple of words on the detection of photons
So the energy of photons is measured well in the CDF calorimeter. To understand how the measurement is done, we need to discuss for a second the physics of the interaction of photons with matter.
Photons, also known as gamma rays, do not leave a signal in the inner tracking system of CDF -a combination of silicon detectors and a multi-wire chamber- because they are electrically neutral: most of them traverse without interacting the five thin layers of silicon, and a fortiori the gas vessel. They also do not get deflected by the strong magnetic field: so they plunge straight into the dense layers of lead which make up the electromagnetic calorimeter; in the photograph above, they enter from the bottom of the wedge, traveling upwards.
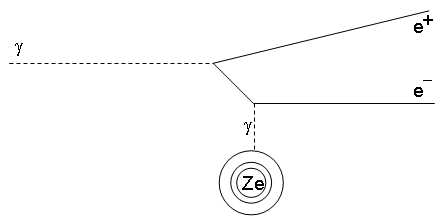Lead has a high atomic number Z, such that its nuclei produce a large electric field around them: when a photon passes close to a lead nucleus, it interacts with its electromagnetic field as shown in the graph on the right. The result of this interaction is called "pair production": the outcoming electron and positron inherit the energy of the originating photon. Note that the photon cannot undergo pair production in the absence of a source of the field, the circle labeled "Ze" at the bottom: the process 
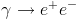does not conserve energy and momentum by itself!
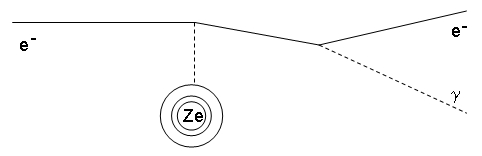The produced electron and positron soon interact with another nucleus , producing an additional photon by what physicists call with the German word bremsstrahlung: braking radiation. The electron is "deflected" by the electromagnetic field, and its change of direction produces a quantum of radiation. Again, this process (shown on the left) is only possible if there is a heavy nucleus that "absorbs" the imbalance in four-momentum of the process. 
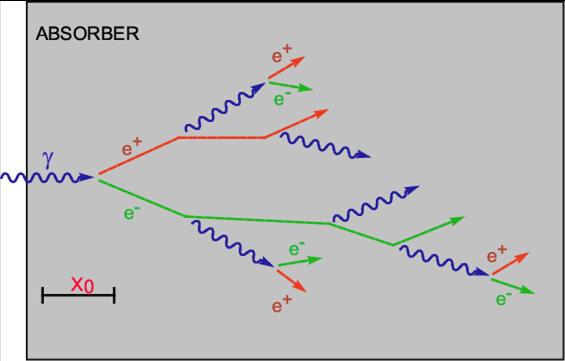The result of the consecutive processes of pair production and bremsstrahlung is that the original photon produces a cascade of secondary particles, as shown in the sketch on the right. By measuring the amount of light that the electrons and positrons yield when traversing the layers of scintillating material, it is possible to precisely determine the total energy of the incoming originating gamma ray. That is because of the direct proportionality of the photon energy with the number N of secondary charged particles produced, and the proportionality between the latter and the light yield which reaches the photomultipliers.There is a lesson to take home from the study of the above physical processes: if the energy is proportional to N, and if N is governed by Poisson statistics, as it is, then since the typical fluctuation of N is its square root, we get that the uncertainty in the energy of the photon scales with the square root of the energy! This so-called "stochastic term" in the energy resolution is what dominates the 2.4% resolution on the Higgs boson mass shown above -a critical number for this search!
The CDF analysis
There are many details in the CDF analysis, but most of them need not concern us here. The critical thing is to manage to select a sample of events with two energetic photons as pure as possible. Purity is essential, because the signal is tiny!
The detection and measurement of a energetic photon therefore implies the following ingredients: a localized, large release of energy in the electromagnetic calorimeter; and no charged tracks pointing at the energy deposit. The requirement that the energy "cluster" be isolated from nearby activity also helps rejecting background from hadronic jets. A candidate diphoton event is shown in the event display below.
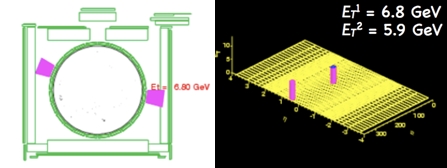
On the left you see a transverse cut-away of the CDF detector. The central tracking system, which lies at the center of the circle, sees no charged tracks at all -in particular, none pointing at the purple energy deposits in the calorimeter. On the right, you see the calorimeter "unrolled" along the rapidity axis, with the two clean energy towers sticking out. This is most likely a clean diphoton event, but backgrounds are nasty, and photons are rare objects in hadron collisions: the possibility that the two photon candidates are the result of the fragmentation of two quarks, leading to mostly neutral particles, is significant.
So backgrounds are an issue. But they cannot really be separated much from the signal after clean photon candidates are selected. The search, in fact, does not employ an ultra-sophisticated multi-dimensional method to enrich the sample with signal. All that can be done is to search the invariant mass distribution of pairs of photons for a narrow bump! In fact, most of the selected events are contributed by QCD background.
The method to assess the presence of a Higgs decay in the data is to exclude a narrow window in the mass distribution, fit the background shape with a suitable parametrization, and then extrapolate and compare the expectation in the signal window with what is actually observed. This method is described graphically in the figure below.
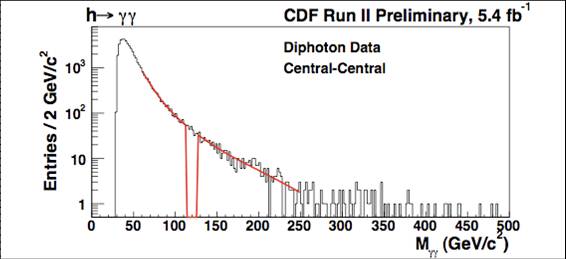
The black histogram shows how the diphoton candidate mass for experimental data is distributed. The red curve is a fit which excludes the mass region around 120 GeV,which is where the signal is sought in this particular case. A comparison of the counts expected for the background with the actual number of events seen in the excluded window provides a test for the presence of an excess of Higgs decays.
Unfortunately, there are no excesses anywhere in the spectrum. Of course! CDF did not in fact expect to see any, at least not from standard model production of Higgs bosons. In fact, the search is not sensitive enough to detect five events! Still, a signal 20 times larger would have produced a detectable deviation. This is not observed, so the authors proceeded to place 95% confidence level limits on the rate of Higgs production entering their selection. What they actually do is to divide the limit found on the signal cross section by the expected cross section for Higgs production. The limit is thus on the "R ratio", which -if it went below 1.0- would imply that the standard model Higgs boson is non-existent at that mass value. No such thing happens, of course: the limit is at R=20 or above, as shown below.
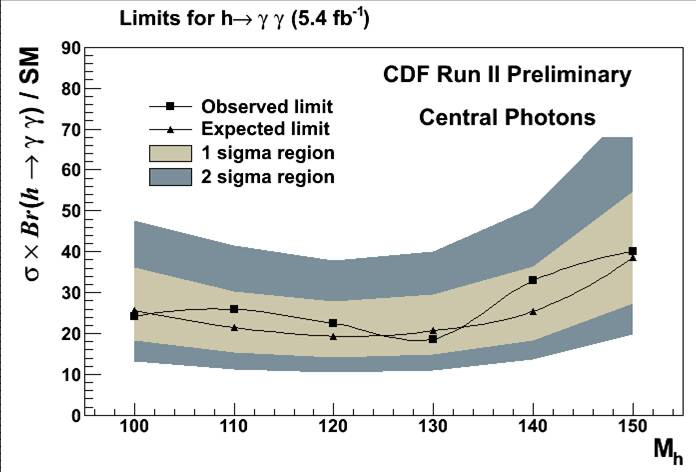
The observed limit is shown by the black squares, and it agrees well with the one that the authors expected to obtain, given the methodology of the analysis and the size of the analyzed dataset.
A last figure, which clarifies how the signal would look like in the mass distribution if its production rate was much larger than the standard model expectation, is provided below.
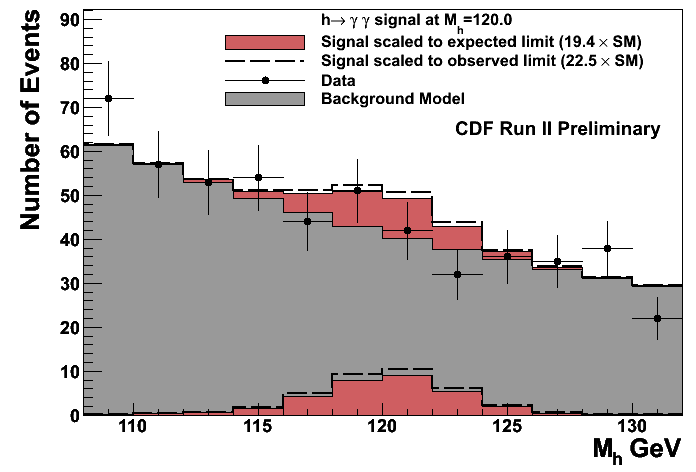
Here the signal is shown in red. The background is in grey, and the CDF data are shown with black points with error bars. The signal shown corresponds to the one that CDF was able to exclude at 95% confidence level, for a Higgs mass of 120 GeV: it is about 20 times what the standard model predicts.
This analysis fills a visible gap in the spectrum of Higgs boson searches that the CDF collaboration has performed with its first five inverse femtobarns of collected proton-antiproton collisions. I am thus very pleased to congratulate with the authors: Karen Bland, Ray Culbertson, Jay Dittmann, Craig Group, and Jamie Ray. Those of you willing to get more details on the search and a public document describing the nitty-gritty details are advised to please follow this link.
Comments