If you are familiar with this blog, you may have noticed that I have often expressed my belief of how the idea of a fourth (or a fifth, etcetera) generation of matter fields is insufficiently pursued both in theoretical and in experimental physics. As nice and "perfect" the number three is, it is really hard to believe that there are just three generations of quarks and leptons. Why so, indeed ?
When the LEP collider experiments ALEPH, OPAL, L3, and DELPHI conclusively determined that there are exactly three kinds of neutrinos with mass below 45 GeV -lighter than half the Z mass, that is, such that their presence would influence the natural width of that particle- the above question became unfashionable: if only three neutrinos exist, the same must apply to charged fermions and quark families, otherwise a very nasty theoretical problem will make the theory inconsistent. However, since neutrinos have later been demonstrated to have a non-zero mass, albeit a small one, there is no real reason to believe that the LEP measurement is a constraint to the number of generations: one may envision that only three neutrinos have masses below 45 GeV, while others are more massive, making the Z decay insensitive to them.
Experimentally, masslve particles belonging to additional generations of matter are not excluded by direct measurements, although they do appear to be indirectly disfavoured by precision electroweak measurements. Those indirect constraints however depend on the validity of some unforced assumptions. Nature (the bitch, not the magazine) might certainly choose to ignore those assumptions.
All in all, the motivations for the search of a fourth kind of quark are quite convincing to me. Fourth-generation quarks produced in high-energy hadronic collisions would manifest themselves in spectacular decays involving several heavy objects. Take a b' quark, a member of a fourth generation of matter, with charge -1/3, and further assume that its mass is above 260 GeV (past searches have excluded the existence of b' quarks with mass below 338 GeV). If a pair of such objects were produced at the Tevatron, they would most likely yield in their decay two W bosons and a top-antitop quark pair. The top quarks would in turn decay immediately into two W bosons and two b quarks, bringing the total count of W bosons to four! The decay of this unheard-of crowd of W bosons would create a firework of energetic leptons, neutrinos, and hadronic jets. This ain't SUSY, but such a decay chain has nothing to envy to the classical cascading of squarks or gluinos into sleptons and neutralinos.
But let us not stray. Instead, I should perhaps remind you here how a W bosons disintegrates. The W is a quite democratic particle: it decays with equal frequency into all the possible lepton pairs and quark pairs that are energetically allowed. Electron-electron antineutrino, muon-muon antineutrino, and tau-tau antineutrino pairs are equally likely; down-antiup and strange-anticharm quark pairs are three times more likely than the lepton pairs, because they exist in three colour-anticolour combinations. So there are a total of nine possible decays: six of them involve quarks, and one each involve electrons, muons, and taus. What this boils down to, when we consider four W bosons and we ignore for simplicity the difficult tau-lepton signature, is the following scheme:
- Four decays to electrons or muons: these produce a striking final state, but they unfortunately happen with a probability of (2/9) to the fourth power, or only once in 400 times.
- Three decays to electrons or muons, plus one decay to jet pairs: the relative rate of this decay can be computed by taking the product of 4x(2/9)x(2/9)x(2/9)x(6/9), where the three (2/9) factors are due to the chance of decay to electron-neutrino or muon-neutrino pairs, and the 6/9 factor tracks the quark-antiquark decay. The factor of four is combinatorial, accounting for the fact that any of the four W bosons may yield the jet final state, without us noticing any difference. With a pocket calculator you may verify whether I am still capable of multiplying numbers by heart: I speculate that the product amounts to one part in 33 or so. Again, this is a spectacular signature yielding two jets, three leptons, plus neutrinos -not to mention the two additional b-jets produced in the top pair decays- but the chance of its occurrence is small.
- Two decays to electrons or muons, plus two decays to jet pairs: this is more common. Now the combinatorial factor is trickier: you may have bosons 1 and 2 decaying to jet pairs, or 1 and 3, or 1 and 4, or 2 and 3, or 2 and 4, or 3 and 4: six combinations. The total probability of the decay is 6x(2/9)x(2/9)x(6/9)x(6/9), or about one eight.
- One decay to electron-neutrino or muon-neutrino, and three decays to jet pairs: now this is quite frequent: the probability is 4x(2/9)x(6/9)^3, or little more than one fourth.
- Finally, we consider the fully-hadronic mode, involving eight jets. This happens with a probability of (6/9)^4, or one fifth! We discovered something here: the fully hadronic decay of W bosons is not the favoured one, if we have at least four of them.
So we may summarize the above facts in one sentence: because quark decays are more frequent, it makes sense to search for these decays of W bosons. However, it is convenient to search for events where at least one W boson yelds an electron or a muon: not only does the latter allow the efficient collection of such signal events at trigger level, but it also makes the total branching ratio higher!
The CDF experiment searched precisely for that final state of b'-anti b' production, and now you understand why. But let us give a look at a Feynman diagram of that firework-like decay chain. It is shown below.
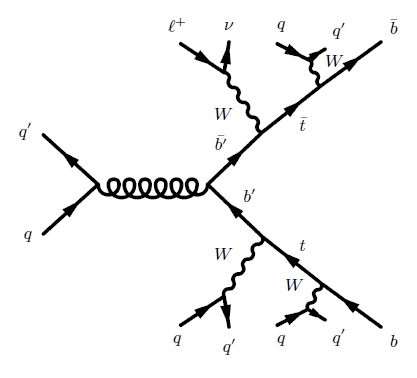
Quite impressive, if you ask me. Still more impressive would be the actual signature one would observe in the detector: up to eight jets all directly coming from energetic quarks emitted in the hard subprocess, plus a lepton and missing transverse energy from the neutrino. True, the missing energy would hardly be significant, given the large amount of energy from the jets that needs to be detected and measured in the calorimeter. Let me explain.
When a W decays to a lepton-neutrino pair, the neutrino escapes the detector unseen, with its bounty of about 40 GeV of momentum. 40 GeV is half the W boson mass, and we are neglecting boost factors and other subtleties, because I am about to produce an order-of-magnitude argument here. Imagine that all produced bodies travels in a direction transverse from the beam line: this is a very incorrect assumption but it allows us to focus on the issue at hand. On the transverse plane, the sum of momenta of all bodies must total zero. If we were capable of measuring with perfect precision the energy of all bodies but we failed to see the neutrino, we would have a 40 GeV imbalance: a smoking gun that the neutrino has left unseen, and a quite distinctive feature of the signal events, likely useful to discriminate backgrounds.
Now, the accuracy with which we measure the total sum of transverse momenta depends on the energies of the bodies we measure. That is because our calorimeter, as good as we managed to build it, has an intrinsic resolution which usually scales with the square root of the detected energy. If the total detected energy is 100 GeV, the missing transverse energy will be known with a uncertainty of about 10 GeV; if it is 400 GeV, the uncertainty will be of about 20 GeV; and so on.
Now we are confronted with the case of the decay of two 400-GeV bodies, the two b' quarks. If all their mass went to transverse energy, we would have about 800 GeV of detected energy in the calorimeter: this would give a rather imprecise measurement of the missing transverse energy, one with a uncertainty of about 25-30 GeV. A 40-GeV neutrino does not provide such a striking signature in these conditions: its momentum could be entirely washed away by an imprecise measurement of some of the energetic jets produced in the decay!
Because of the above fact, missing energy is not such an useful tool in the hunt for massive fourth-generation quarks we are considering. CDF does select events with at least 20 GeV of missing transverse energy for the search, but then they do not rely too much on that variable alone to isolate backgrounds not containing neutrinos. Instead, the discriminating variable of choice is taken to be the total sum of transverse energies of jets, lepton, and missing energy. This variable is called "Ht", and it is a good indicator of how "hard" was the collision that took place.
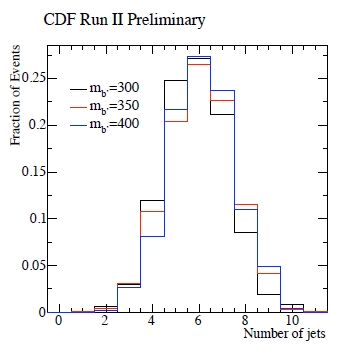 Events are classified according to the number of jets that are observed with transverse energy above 15 GeV, in a central region of the detector. Since it is quite likely that at least one or two of the quarks emitted in the complicated decay chain will be emitted at small angle with respect to the beam line, the nominal signature of eight jets accompanying the lepton and missing Et is loosened: a significant fraction of signal events will only produce five, six, or seven jets in the detector, as shown in the figure on the right. Different hypothesized b' masses produce slightly different distributions, but the message is clear: the most frequent instances involve 5, 6, or 7 jets.
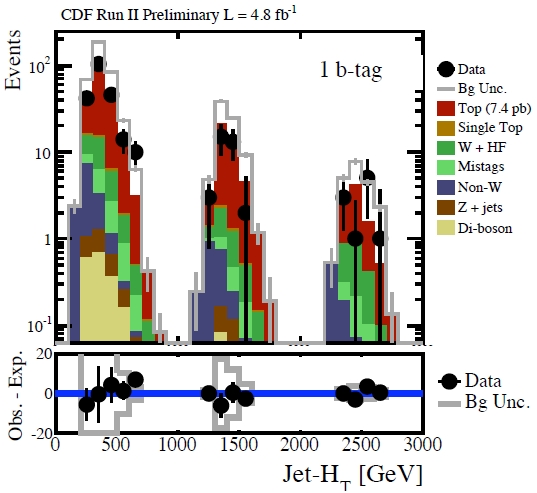
Events are classified according to the number of jets that are observed with transverse energy above 15 GeV, in a central region of the detector. Since it is quite likely that at least one or two of the quarks emitted in the complicated decay chain will be emitted at small angle with respect to the beam line, the nominal signature of eight jets accompanying the lepton and missing Et is loosened: a significant fraction of signal events will only produce five, six, or seven jets in the detector, as shown in the figure on the right. Different hypothesized b' masses produce slightly different distributions, but the message is clear: the most frequent instances involve 5, 6, or 7 jets.Now we must not forget that these events feature top quark decays: these yield two b-quark jets, which can be identified by the long lifetime and successive decay of the hadron incorporating the b-quark. CDF divides the data according to the number of b-tags, and fits the Ht distributions to search for a b' signal. The data is shown in the figure below (which represents the 1-b-tag category) as black points, and it is compared to the sum of contributing backgrounds; these include top production and QCD processes, as well as single-top production and various minor processes involving bosons. Needless to say, the data agrees with background predictions, and no excess is observed in any of the nine categories (5, 6, or 7+ jets; 0, 1, or 2 b-tags). The two distributions of Ht on the right are shifted by 1000 and 2000 GeV, respectively, to divide events with 6 or >=7 jets from events with exactly 5 jets.
In the end, CDF is able to set a limit on the production rate of the fourth-generation quark; from it, using the theoretical cross section for b' production, a lower limit on the b' mass can be extracted. This amounts to
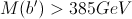 , at 95% confidence level. The graph below illustrates the extracted limit in the cross section versus mass plane; the red curve shows the cross section limit; the dashed line is the theoretical prediction for the signal cross section. Where the two cross each other, there you have your lower mass limit. You may jolly well ignore the Brazil-flag band, which describes the expected result in the absence of a signal: nothing much can be learned from it in this case.
, at 95% confidence level. The graph below illustrates the extracted limit in the cross section versus mass plane; the red curve shows the cross section limit; the dashed line is the theoretical prediction for the signal cross section. Where the two cross each other, there you have your lower mass limit. You may jolly well ignore the Brazil-flag band, which describes the expected result in the absence of a signal: nothing much can be learned from it in this case.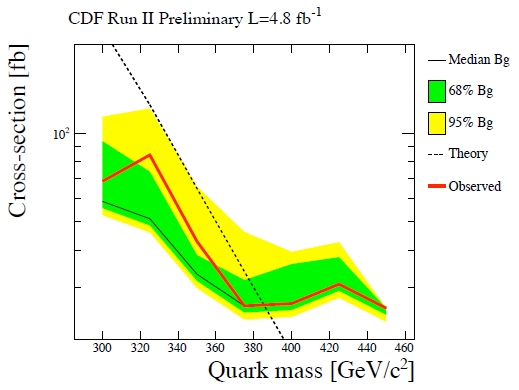
So CDF says, no fourth-generation b' quarks for today. Good to know, but the LHC next year will push the limit much higher, or hopefully see a first hint of a signal. Yeah, right. If it did, I would lose a 1000$ bet. You read correctly: I bet against new physics of any kind from the first few inverse femtobarns of LHC data, a few years back. 1000$ or new physics ? Hmm. 1000$ is a lot of good wine, for instance. New physics would make me ecstatic for a while, but a couple dozen bottles of Amarone also would. Tough choice. I am sure that Nature will choose wisely, though.





Comments