Quarks: properties and decays
According to the Standard Model of particle physics, matter at the subnuclear level takes two forms: quarks and leptons. What distinguishes these particles is that the former, in addition to an electric and a weak charge, carry units of an additional quantum number called colour charge. This peculiar kind of colour comes in three kinds, say red, green, and blue; and each has positive and negative units: quarks carry colour, antiquarks carry anti-colour.
The colour field of which they are a source binds quarks in colour-neutral combinations: a quark-antiquark pair with opposite colour is called a meson, and a combination of three quarks of the three different colour charges is called a baryon. Both mesons and baryons are colour-neutral.
The colour-neutral combinations of quarks are fundamental for the existence of all matter structure we know. But quarks also carry additional quantum numbers, which distinguish them and allow us to categorize them in three different "generations": up and down-type quarks belong to the first generation, charm and strange-type ones belong to the second, and top and bottom-type ones belong to the third. The up quark is the least massive, so it is stable, being unable to decay into anything lighter; all others are instead short-lived.
The decay of a heavy quark occurs when the particle "emits" a weak vector boson, the W particle. The W is the true object of desire of ancient-times alchemists, since it is the key of transmutation of matter. For example, a down quark inside a neutron may turn into a up quark by emitting a W boson: the latter immediately decays into an electron-neutrino pair, and the neutron has turned into a proton - changing an atomic nucleus of atomic number Z into its Z+1 neighbor in the periodic table of Mendeleev.
The above mechanism, radioactive decay (also known as "beta decay" to be more precise), is the one responsible of the turning of quarks of any kind into lighter ones. Experiments searching for new heavy quarks (heavier than the massive top quark, because lighter ones would have already been detected by earlier experiments) usually assume that this continues to work, although interesting searches have also been performed which hypothesize that Z bosons can be mediating the transmutation. ATLAS looks for W boson mediated decays in its new search.
If a quark is heavier than the W boson, its decay to a lighter cousin occurs at blitzing speed. There are two ingredients that determine this speed: the mass difference of the initial body and its daughters (the larger this is, the faster the decay takes place) and a factor called "Cabibbo-Kobayashi-Maskawa matrix element". Most searches for new heavy quarks, such as the one we are about to discuss, assume that such factor is not too small, otherwise the heavy quark would spend a significant amount of time inside a heavy colourless hadron before disintegrating into lighter particles.
But why additional quark families ?
Soon after the fourth quark, the charm, was discovered in 1974, physicists grew convinced that there needed to exist a third family. This would accommodate in a simple theoretical setting a funny property of weak interactions observed back in 1964, the phenomenon of CP violation. Kobayashi and Maskawa had in fact already postulated in 1970 that if quarks were real, then to explain CP violation in weak interactions there needed to exist three generations of quarks, at a minimum.
At a minimum. So you could think that by the time the sixth quark (the top) was discovered, in 1995 by the CDF and DZERO collaborations at the Fermilab Tevatron collider, one could have thought that more were in store. However, by then we were cooled down by the result of a study of the "invisible" Z boson decays: the LEP collider had produced millions of Z bosons in electron-positron collisions at 91 GeV, and only 20% of them had been seen to be "missing", decaying into three different kinds of neutrino-antineutrino pairs. If matter was made up of more than three generations, one would have expected more missing Z events.
Three kinds of neutrinos for a while meant the end of the hopes for a fourth generation of matter fields, including quarks -one could not introduce an additional quark family in the theory without adding a corresponding lepton-neutrino pair, lest the theory would become utterly inconsistent. But then, there came the discovery by SuperKamiokande, in 1998, that neutrinos do have a tiny but non-zero mass!
If neutrinos do have mass, then a fourth kind of neutrino might exist, and be more massive than half the Z boson mass: in that case, no contribution would be expected to invisible Z decays. Everything can be consistent again, with four, or five, or who knows how many more generations of matter.
Things are not so simple, however. Although the Z cannot decay into fermion pairs of mass larger than 45 GeV, the presence of these particles in virtual electroweak processes -ones to which the physics of Z bosons is very sensitive- would modify the observed values of measured quantities that LEP and other experiments have studied with care in the course of the last thirty years. The so-called "oblique" parameters would not be so oblique, the Z would take offence and decay more asymmetrically, and other electroweak processes would misbehave.
But we are well in the realm of detailed model predictions. And theoretical models, of course, are called such because they are only a description of reality. What if those models are incorrect ? Maybe the Standard Model could accommodate new families of quarks and leptons without requiring such a huge overhaul, after all.
The ATLAS search
So it makes sense for the LHC experiments to search for these new heavy particles. ATLAS did it by assuming that new quarks get pair-produced in QCD interactions (which occurs if new quarks are coloured as the good old ones), and that they decay by charged-current weak interactions -W exchange- as all others.
The picture suddenly becomes very close to that of top quark pair production and decay: the only difference is that the top quark decays into a W boson and a bottom quark, while the new hypothetical fourth-generation quark is taken to decay into a W boson and any kind of light quark. In fact, not knowing the relative value of the Cabibbo-Kobayashi-Maskawa mixing matrix for these new quarks, one must keep open the possibility that the heavy quark may decay into any of the lighter ones; except the top, which is too massive and would require a separate treatment.
So ATLAS looks for events with two W bosons and two hadronic jets, without trying to characterize the latter as coming from bottom-quark hadronization (as is instead the case of top quark searches). The cleanest final state involves the decay of each W boson into an electron-neutrino or a muon-neutrino pair, because high-energy electrons and muons are rare in hadronic collisions.
Once one selects events with two high-momentum charged leptons, two jets, and significant missing transverse energy (the latter due to the neutrinos), backgrounds are mostly due to leptonic Z decays and top pair production.
The Z decay background is reduced by requiring that the missing energy is large when the two leptons have the same flavour (electron-positron or positive-negative muon pairs), and that the lepton pair mass is outside of the 81-101 GeV window.
To discriminate the heavy quarks from top production, it would be good to reconstruct the mass of the decaying object: top has a mass of 175 GeV, while here we are looking for heavy quarks of masses above 250 GeV, so constructing an observable quantity connected to the mass of the quark would allow a good separation. But how to do this in dilepton decays, which involve two neutrinos ? We do not know where the neutrinos have gone, since we can only measure the combined transverse component of their momentum. A kinematical fit to the quark pair decay is insufficiently constrained, given that the constraints (quark and antiquark mass equality, plus known mass of the W bosons, plust total transverse momentum equal to zero) are fewer than the unknowns (mass of the heavy quark, and neutrino momenta).
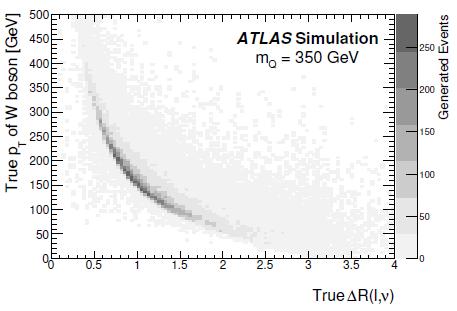ATLAS notices that the heavy quark mass causes the W bosons emitted from its decay will have a large boost: this causes the neutrino and the charged lepton produced in the subsequent W boson decay to travel close in angle, as exemplified in the figure on the right (on the abscissa is the angular separation in radians, on the y axis the transverse momentum of the W; the population shown refers to a heavy quark of mass 350 GeV). One can therefore assume that the neutrinos have been emitted in the direction of the leptons, and this suffices to allow a kinematic fit to the unknown heavy quark mass to converge meaningfully.The resulting "collinear mass" is shown for different heavy quark masses in the figure below: a good separation of signal and top background is achieved.
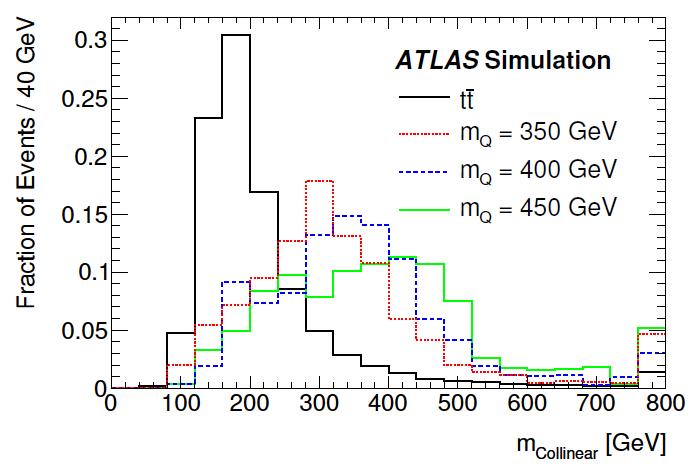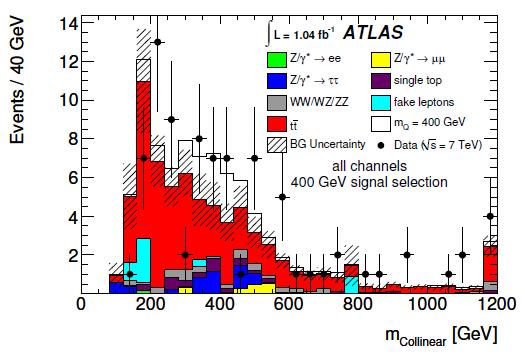
A selection of the data aimed at maximizing the "significance" (this is the term used in the ATLAS paper) S/sqrt(S+B) is then performed separately for each different mass hypothesis. The selection is based on the event kinematics and is derived from a comparison of simulated signal and background events. I will move some criticism to this criterion at the end...Finally, a likelihood fit is performed on the collinear mass distribution for each mass hypothesis. This allows to put a limit on the number of signal events present in the data, using the CLs criterion -basically a prescription on how to compute the probability of the observed data given a hypothesis on the number of signal present in it. Below you can see the mass distribution in the case of the search for a 400 GeV quark.
The set of upper limits in the number of signal events is translated into a corresponding set of upper limits in the signal cross section, and this in turn allows to obtain a lower limit on the mass of the hypothetical quarks by producing the graph below, which shows the cross section upper limit versus mass curve (in purple) along with the theoretical prediction for the signal cross section, which is also a (of course decreasing) function of the quark mass. The upper limit observed is complemented by a "brazil band" describing the possible ranges of limits that the search methodology was expected to return.
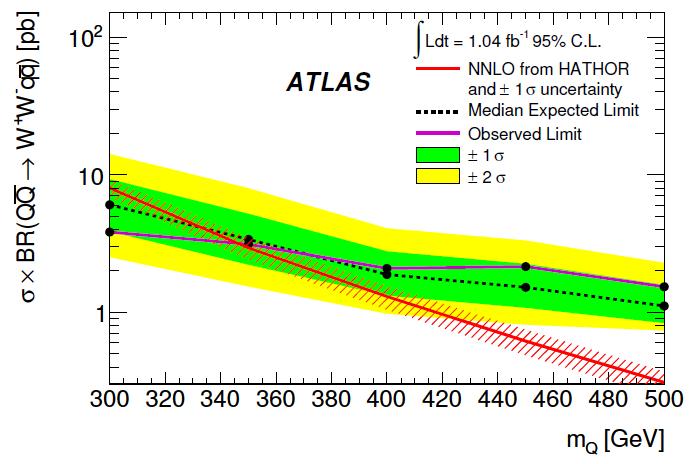
The point where the theoretical curve meets the upper limit is found for a quark mass of 350 GeV: ATLAS therefore rules out lighter new quarks, at 95% confidence level, under the assumption of 100% decay of the heavy quark into Wq final states.
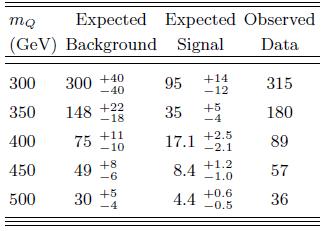The above results appear rather mysterious to me. If I look at the table of expected background events and observed data events for the various selections (see right), I see that ATLAS observe more events than they expect, in all cases. The departures are mild -of the order of one to 1.5 standard deviations- but they are all in the same direction; while the observed limit is seen to be below the expected one, for quark masses of 300 and 350 GeV. How come ?
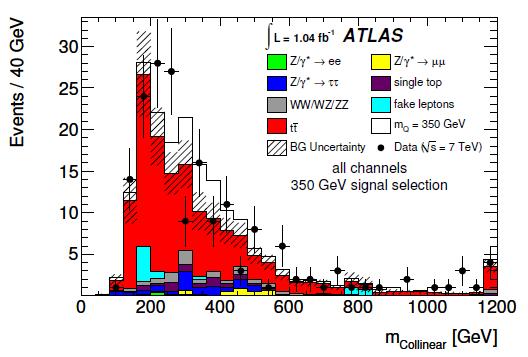The fact that collectively one sees more events than backgrounds does not mean that one must by force fit a positive signal in a likelihood fit using also the shapes of the distributions and background uncertainties; but it is highly peculiar to see the opposite behaviour -that is, obtaining a better result than expected, in the presence of an excess of data. At 350 GeV, ATLAS expects 148+22-18 events and sees 180. The relevant histogram is the one on the left.I might be wrong (and I have only read very quickly the ATLAS paper, so I might be overlooking something) but it seems strange to me that ATLAS obtains a better-than-expected limit by fitting the above distribution. I hope my ATLAS colleagues will correct me and clarify the observed behaviour.
The sting is at the end: a mild criticism of the ATLAS analysis
Besides the request for clarification just discussed, I promised above I would have something to say about the way the ATLAS search is optimized, so let me do that here. In general, the function Q=S/sqrt(S+B) is a good indicator of how much a signal will "stand out" in a given set of data, if one performs a counting experiment where one's background prediction is B. The reason is that upon observing a total number of events N=B+S, the standard deviation on N -a Poisson random variable- is sqrt(N)=sqrt(B+S), so the number of standard deviations separating the observation N=B+S from the prediction B is indeed Q=S/sqrt(B+S).
It is well-known that the above reasoning fails when N is small, because the approximation implicit in using the standard deviation of the Poisson distribution rapidly becomes invalid. Leaving aside statistical jargon, what happens with small event counts is that there is an added benefit in making B as small as possible, with respect to the above calculation. Let us take the number of background and signal events in the mass plot above as a starting point for a totally didactical example.
In the 280-480 GeV range, the one most populated by signal (and thus the region to which the ATLAS likelihood fit is most sensitive), I count about 10 expected signal events and 23 expected background events. It is fair to say that the likelihood results will be most affected by the amount of signal and background in that region, for the MQ=400 GeV hypothesis.
S=10 and B=23 corresponds to a Q-value of S/sqrt(S+B)=1.74. Let us take as a possible different working point one obtained by making a purely hypothetical tighter selection, causing (say) S=5 and B=4 events in the same mass region: a higher signal-to-noise ratio would be here paid by a worse value of Q=5/sqrt(9)=1.67. So ATLAS, maximizing Q for their "optimization", would choose to stick with the baseline selection of S=10 vs B=23, even if some different choice of cuts were to offer the chance of settling to the tighter, higher S/N, working point.
But if I naively compute the probability that 33 or more events are observed when 23 are predicted, I get a p-value of 3%; while if I compute the probability that 9 or more events are observed when 4 are expected from backgrounds, the p-value is of 2%: in other words, the lower-Q situation of S=5,B=4 should be privileged with respect to the higher-Q situation of S=10, B=23 that ATLAS chose in its "optimization", because the smaller S=5 event signal would "stand out" more -the background hypothesis would be more disfavoured by the data. This is just an example to stress that for small event counts, what matters is the S/N ratio rather than the Q-value.
The literature is full with possible improvements to the rather rough Q-value formula employed by ATLAS, which address the problem I highlighted above; nevertheless, all these "approximate" pseudo-significances may represent a meaningful way to optimize one's analysis only in the lack of the possibility of carrying out a full pseudo-analysis which would account for the fitting method, the related systematics, and all the other nuisances that make a end result better than another. What I wish to stress is that the word "optimization" should be used with paucity and caution in similar situations !
Comments