Most of the optimization tasks I am concerned with in fundamental science live in very high-dimensional spaces, spanned by continuous parameters whose interconnection is unfathomable by the human mind. This is the case, for example, of choosing the geometry and materials of a particle detection system for a new experiment. I can formalize that task by simply saying that given a total budget B, and a precisely defined objective function U (why not O? Because I write "objective function" but I always think at in in terms of the experiment's Utility), you want to find the arrangement of detection elements and materials that guarantees a maximization of U under the constraint that the total cost does not exceed B.
What is your objective?
The precise definition of U is absolutely crucial, and we could write books about it (I don't even bother searching and fear no error in saying somebody certainly has; I limited myself to writing an article about it, see here). But here, let us suppose it is a well-defined function of your apparatus performance (e.g. in terms of the precision of the measurement of particles crossing it, in some sense that one can better define - but we need not do so here).
What one is left with is a multi-dimensional continuous space to scan, where U must be evaluated in search of its absolute maximum value. Such a problem is typically intractable via likelihood maximization. That means the likelihood function does not exist because the physical processes that generate the data are stochastic. So one must sample the space of configuration parameters, evaluate U, and repeat until the max of U is found or the Universe comes to an end, whichever comes first. Hint: typically it will be the latter to happen first.
A solution to this intractability comes from machine learning, where problems with billions of parameters are solved routinely: e.g., the training of large language models involves setting weights and biases of gigantic deep learning systems. Granted, in those tasks one never really cares much if the absolute maximum of the utility (or the absolute minimum of the loss) is precisely located: one is happy with having "approximately" solved the problem, as typically there exists a broad peak where the highest utility values lay, and as long as you find a place near the peak you can call yourself happy. But the same may well happen for experiment optimization. So why not borrowing the methods used there?
Indeed, what one can do is to create a suitable continuous model of the performance of an instrument as a function of its design parameters, and optimize the parameters by stochastic gradient descent (SGD) exactly as is done in the training of LLMs or other deep learning tasks. One will not be concerned too much by the imprecise nature of the model: as long as it more ore less captures the correct interplay of the parameters, it is a good bid. There will always be time after a honest candidate of a optimal solution is found, to fine-tune and re-check the performance with full simulations that set aside the imperfect model.
With the MODE collaboration we have been following the above scheme in a variety of experiment optimization tasks during the past five years, and we have a few interesting outcomes to be proud of. In all these instances, we unleashed the power of SGD in the large space of design parameters, and reaped the benefits of the automatic "rolling up" of the configuration to the extremum of the utility. We did it by using what is called "differentiable programming" But this technique cannot be used in all problems: there are discrete parameters, too!
Discrete parameters
And there are many. For example, the number of elements of a detection system is an integer, not a real number; the number of signals a particle leaves behind in traversing an instrument is an integer; the number of electronic channels you connect to the detector is an integer. How to deal with discrete parameters? No, the answer is not "hell SGD" - gradient descent requires you to compute the gradient (doh) of the utility function with respect to a variation of the value of the parameter you are considering. If the parameter is "number of detection layers", the gradient is mathematically ill-defined, and SGD does not work out of the box.
We can, in many instances, fix the discreteness issues by "analytical continuation" of integers into the real domain. For example, if you have a detector made of two detection layers and a particle goes through it, it will generate two hits; if you now add a third layer in between, a third hit will be generated. But now, suppose you make the added layer a "phantom" one, which has only a p<1 probability of being there. The third hit will be recorded with the same probability. You are now in a position to compute the gradient of the utility with respect to p, which will tell you whether it is advantageous to grow p toward 1 (make the layer appear) or toward 0 (dump it).
Tricks like the one above are ubiquitous and computer scientists - and now physicists - have been making a living out of them. However, although they can in principle *always* be applied in a way or the other, they can become quite impractical in complex situations.
Hybridization
The alternative is to factorize the problem, and sublet the discrete part of the parameter space to a different optimization engine. SGD will still be tasked with navigating the continuous domain; the other algorithm will instead propose different combinations of the discrete parameter values, and try to learn whether the new proposed values are better than previous ones. So this is the idea: couple reinforcement learning (RL) with gradient descent in a hybrid optimization scheme. Note that RL is hardly the only option: there are tons of learning methods one may use. In general one talks of "evolutionary algorithms" to bundle together a class of tools that explore the parameter space in a sparse way, still being able to sniff the right direction where U is increasing. So why RL? Well, one has to start with something. And the simplest RL algorithms are quite easy to implement!
Now, as I was saying I am a rookie with RL, so when I started to investigate how to extend the search space to discrete parameters in the SWGO detector optimization problem I have been fiddling with as of late (see here for interim results), I started easy. There is an algorithm called "multi-armed bandit" that makes proposals for the value of the discrete parameters following a simple scheme, and upon receiving an evaluation of the resulting performance (values of U resulting from those choices, in our case), it stores that outcome in a memory. New proposals are made based on some probability distribution function that gets updated based on how successful previous combinations of values were in previous attempts, and little by little the system "learns" what works and what doesn't.
It took me a while to implement the above concept in my SWGO optimization code. The reason is not the RL algorithm itself, as that is quite simple; rather, the original SGD pipeline is rather complex today, and the code has become over 18,000 lines long. Also, it is written in a very chaotic way, as you would expect from a physicist: it works, but it is hard to modify it without breaking something.
Eventually, I think I have it - a software pipeline that models gamma ray and proton showers in the atmosphere in a continuous way, determines the signal left by secondary particles on hundreds of detector units on the ground, reconstructs the shower characteristics from those signals, classifies the signal as a gamma or proton, and computes a utility function. At that point, the original code used to propagate the derivatives of the utility function with respect to the movement of the detection units on the ground, to find their optimal positions. Instead, now the program also proposes discrete changes to the layout (in terms of number of units deployed, number of triggering stations collecting the signal, and so on). A bunch of different utility values are thus obtained, and the RL algorithm sorts them out to decide what configuration to propose at the next epoch. Then SGD kicks in and moves stuff around.
As you can see in the clip below, the whole thing works. The gif shows a number of different things, but you can just observe the top left graph, which shows how the utility (y axis variable) grows as the epoch number (x axis) increases; and the red points (detection units) in the second graph of the top line (or the second of the bottom line) move around by SGD and sometimes increase or decrease in number when RL decides so.
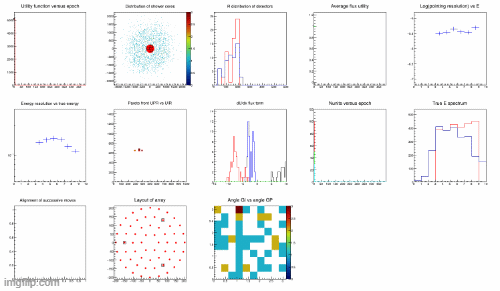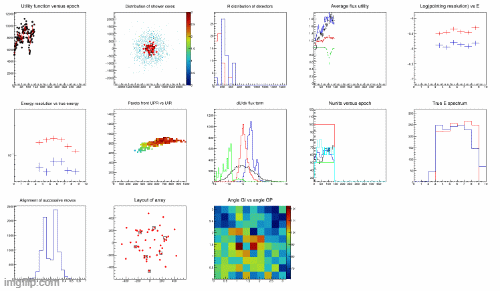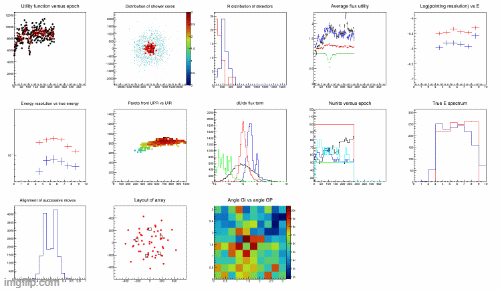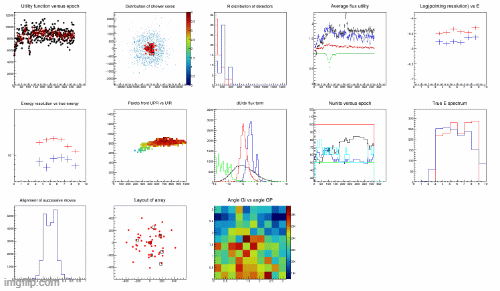
I have a lot more to learn about RL, but I am already satisfied by observing that a very simple concept - sampling from a dynamically varying probability density function, that is updated based on the outcomes of previous samplings - does produce the digital equivalent of "learning".
My final considerations
If you are used to read this blog you might have already been exposed to the fact that I have no big respect for human intelligence, as I liken it to the intelligence shown by language models these days. There is in my opinion no conceptual difference in the way we form sentences - and thence form reasoning with them - and LLMs do. But that idea is expanded in a different article. Here, however, I can draw a parallel with RL. We, in fact, as any other animal around, mostly learn by trial and error. We may be die-hard Classical Statisticians by belief and scientific practice, and yet we all function by Bayesian updating of our beliefs. The same idea, coded in very simple ways, provides powerful realizations of the same learning experience in silico. What makes us human different? Of course, the richness of our sensorial experiences, the self-reflection and consciousness, bla bla. But down to the bare bones, we are working by the same simple mechanisms that power learning of a 100-lines-of-code RL routine.
I also believe that artificial intelligence is the next evolutionary step of humankind. We will one day integrate with machines, and this will enable us to travel through the universe, become a multi-planetary species, and really become free - free from the way we fight for resources on this thin skin on the surface of Earth we call atmosphere. But that will take time.





Comments