Their names dominate, likewise, the history of philosophical reactions to the new physics of the twentieth century, Bohr for having identified complementarity as the chief novelty in the quantum description of nature,(2) Einstein for having found vindication in relativity theory for either positivism or realism, depending upon whom one asks.(3) Famous as is each in his own domain, they are famous also, together, for their decades-long disagreement over the future of fundamental physics, their respective embrace and rejection of quantum indeterminacy being only the most widely-known point of contention.
A well-entrenched narrative tells the story of the Einstein-Bohr debate as one in which Einstein’s tries, from 1927 through 1930, to prove the quantum theory incorrect via thought experiments exhibiting in-principle violations of the Heisenberg indeterminacy principle, only to have Bohr find the flaw in each, after which Einstein shifts his direction of attack, faulting the quantum theory now not as incorrect, but incomplete. In 1935, the Einstein, Podolsky, and Rosen (EPR) paper, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” (Einstein, Podolsky, Rosen 1935) represents the high-water mark of this critique. It is met by Bohr’s deep and devastating reply (Bohr 1935), after which Bohr grows ever more in stature and influence as the sage of Copenhagen, while Einstein slips into senility in Princeton, meddling, perhaps commendably, in the politics of the atomic bomb, but no longer capable of constructive contributions to physics, itself.(4)
That something is seriously wrong with this triumphalist narrative has been remarked upon by various authors for more than twenty years.(5)
More than anyone else, however, it was Mara Beller, in her Quantum Dialogue (Beller 1999) who forced a reassessment.(6) One need not agree with every detail in Beller’s own account of the way in which the community around Bohr in Copenhagen achieved consensus on questions of interpretation in order to appreciate the point that the writing or rewriting of history is, itself, one of the many tools with which communities define themselves and construct consensus. Reason enough always to be just a bit suspicious of any community’s telling its own story.
Some aspects of Beller’s new history I commend; others I do not. I commend Beller’s stressing, like James Cushing before her (Cushing 1994), the role of contingent social and historical circumstance in the achievement of consensus. More than Beller, I find cogency in Bohr’s arguments, but there can be no doubt that the victory of a “Copenhagen” point of view on interpretation is explained, in no small measure, by such factors as Bohr’s control over financial resources through his institute in Copenhagen, by his personal prestige, and even by a conversational manner that some regarded as persistent and others as bullying.
But Beller identifies Bohr as the chief enforcer of a Copenhagen orthodoxy, whereas I think that what later came to be regarded as Copenhagen orthodoxy owed more to Werner Heisenberg than to Bohr. On my reading, Bohr was never a positivist, did not endorse wave-packet collapse, and did not demand ideological conformity among his followers.(7) It was not by compulsion, but by the example of his dogged pursuit of the deep philosophical lessons of the quantum that Bohr created and sustained not a unitary “Copenhagen interpretation,” but what Leon Rosenfeld called the “Copenhagen spirit” (Rosenfeld 1957).
That the standard, triumphalist Copenhagen narrative requires significant revision is, however, as noted, a point upon which I wholeheartedly agree with Beller. It needs revision if only to redress the insult to Einstein. The present paper is a contribution to that revision. I argue that the standard history is wrong not only for the kinds of reasons cited by Beller, but also for the reason that it more or less completely misses the real point at issue between Einstein and Bohr.
Simply put, both Bohr and Einstein understood early and clearly that the chief novelty of the quantum theory was what we, today, call “entanglement,” the non-factorizability of the joint states of previously interacting quantum systems. Bohr embraced entanglement, seeing in it the roots of complementarity.
Einstein rejected entanglement as incompatible with the principle of the spatial separability of systems, a principle that he thought not only a necessary feature of any field theory like general relativity but also a necessary condition for the very intelligibility of science. Everything else is derivative, including Bohr’s defense of complementarity and Einstein’s charge of the incompleteness of quantum mechanics, a charge unsustainable without the assumption of what Einstein termed the “separation principle.”
On this way of revising the history, Bohr still emerges with the better arguments. Here, too, Beller and I disagree. But Einstein’s legacy is rehabilitated, his dissent being seen for what it was: principled, well-motivated, based upon deep physical insight, and informed by a sophisticated philosophy of science.
Why later apologists for Copenhagen orthodoxy preferred the senile Einstein as Bohr’s antagonist is hard to fathom, for Bohr’s defense against Einstein’s critique makes more sense and is more interesting when read as a reply to a good argument rather than a bad one. Putting a debate about entanglement at center stage has the additional salubrious effect of highlighting a still more general failure of the received history of quantum mechanics in the early twentieth century.
It was not just Einstein and Bohr who were arguing about entanglement. Everyone was. That the joint states of previously interacting quantum systems do not factorize and that the quantum mechanical story about multi-particle systems differs, thus, in a fundamental way from the classical story were facts understood by all of the major players, well before Erwin Schrödinger baptized the phenomenon as “entanglement” in 1935, and long before quantum information theory made entanglement the hot, new topic in the foundations literature in the 1990s.(8) Why the standard histories of quantum mechanics have not emphasized this is as puzzling as their penchant for letting caricature take the place of a sympathetic and accurate account of Einstein’s critique of the quantum theory.
Einstein, Bohr, and Entanglement before the 1927 Solvay Meeting
Standard histories of the Einstein-Bohr debate have it beginning in earnest during the personal encounter between Einstein and Bohr at the 1927 Solvay meeting. This was an important confrontation, but to understand what Einstein and Bohr were arguing about then and later, one must understand first their prior confrontations with the issue of entanglement. Einstein had been thinking about the problem for over twenty years, Bohr for nearly ten. From the very beginning, that is, from his 1905 paper on the photon hypothesis, Einstein understood that the emerging quantum theory was likely to incorporate some compromise with the fundamentally classical idea of the mutual independence of interacting systems.(9)
The reason was simple and obvious. Recall that Einstein’s route to the photon hypothesis was via a thermodynamic analogy. Einstein showed that expression for the entropic behavior of radiation in the Wien (highfrequency) regime exhibited the same functional form as the entropy of a classical, Boltzmann gas.
That analogy sustained the inference that radiation in the Wien regime had a microstucture like that of a Boltzmann gas, in the sense that it consisted of discrete, distinguishable, mutually independent, corpuscle-like carriers of the field energy that Einstein dubbed light quanta. In Einstein’s own words:
“Monochromatic radiation of low density (within the domain of validity of Wien's radiation formula) behaves from a thermodynamic point of view as if it consisted of mutually independent energy quanta of the magnitude Rßí /N ” (Einstein 1905, 143).
What did it mean to say that light quanta were “mutually independent”? It meant precisely that the Boltzmann formula applied or that entropy is an extensive property of the radiation gas, for the additivity of the entropy of a composite system is equivalent to the factorizability of the joint probabilities for the differently spatially situated component subsystems occupying given cells of phase space, this latter being the normal way of expressing the probabilistic independence of two events. Again, in Einstein’s own words:
If we have two systems S1 and S2 that do not interact with each other, we can put
S1 = φ1(W1),
S2 = φ2(W2).
If these two systems are viewed as a single system of entropy S and probability W, we have
S = S1 + S2 = φ(W)
and
W = W1 ∙ W2.The last relation tells us that the states of the two systems are mutually independent events.
(Einstein 1905, 140-141)
But this argument works only in the Wien limit. That such mutual independence is thus shown only to hold in the Wien limit and that it is likely to fail outside of the Wien regime is obvious, however much this obvious fact goes unremarked in much of the secondary literature on Einstein and the quantum.
The simple fact is that, from the very beginning, Einstein understood the limitations of the argument and understood that, in general, the radiation field could not be modeled in simple corpuscular terms. If there be any doubt that Einstein understood that mutual independence would not obtain outside of the Wien regime, consider what he wrote to Hendrik Lorentz four years later:
I must have expressed myself unclearly in regard to the light quanta. That is to say, I am not at all of the opinion that one should think of light as being composed of mutually independent quanta localized in relatively small spaces. This would be the most convenient explanation of the Wien end of the radiation formula. But already the division of a light ray at the surface of refractive media absolutely prohibits this view. A light ray divides, but a light quantum indeed cannot divide without change of frequency.
As I already said, in my opinion one should not think about constructing light out of discrete, mutually independent points. I imagine the situation somewhat as follows: . . . I conceive of the light quantum as a point that is surrounded by a greatly extended vector field, that somehow diminishes with distance. Whether or not when several light quanta are present with mutually overlapping fields one must imagine a simple superposition of the vector fields, that I cannot say. In any case, for the determination of events, one must have equations of motion for the singular points in addition to the differential equations for the vector field.
(Einstein to Lorentz, 23 May 1909, Einstein 1993, Doc. 163)
In other words, the idea of wave-particle duality is born out of Einstein’s effort to exploit the metaphor of interference for describing the manner in which light quanta outside of the Wien regime do not behave like mutually independent systems.
Over the next decade, many people in addition to Einstein struggled to understand what kind of statistics was appropriate for quantum systems behaving in such a non-classical manner. An especially illuminating moment in that history is recorded in a series of papers by Mieczyslaw Wolfke, who was Einstein’s colleague in Zurich for a short time in 1913-1914. Wolfke was seeking to understand exactly what kind of independence among light quanta was assumed in Einstein’s 1905 argument, and his remarks are interesting in part because they are based on direct communications from Einstein, himself.In the last of four papers, Wolfke wrote:
In fact the Einsteinian light quanta behave like the individual, mutually independent molecules of a gas . . . . However, the spatial independence of the Einsteinian light quanta comes out even more clearly from Einstein’s argument itself. From the Wien radiation formula Einstein calculates the probability W that all n light quanta of the same frequency enclosed in a volume v0 find themselves at an arbitrary moment of time in the subvolume v of the volume v0. The expression for this probability reads:W = (v/v0)n. This probability may be interpreted as the product of the individual probabilities v/v0 that an individual one of the light quanta under consideration lies in the subvolume v at an arbitrary moment of time. From the fact that the total probability W is expressed as the product of the individual probabilities v/v0, one recognizes that it is a matter of individual mutually independent events. Thus we see that, according to Einstein’s view, the fact that a light quantum lies in a specific subvolume is independent of the position of the other light quanta.
(Wolfke 1914, 463-464)
How deeply the problem of quantum statistics weighed upon Einstein’s soul before 1924 is clear from a far-too-little-known argument adduced by Einstein in 1920 for the purpose of opposing(!) a field ontology of trackable, mutually independent carriers of field energy. The setting is the lecture, “Äther und Relativitätstheorie,” delivered in May, 1920 as the inaugural address for Einstein’s visiting professorship in Leiden, home to Lorentz, whom Einstein held in high esteem.
In what is partly a gesture of respect for Lorentz, Einstein evinces surprising sympathy for the concept of the ether, arguing that, in many respects, the space-time of general relativity has taken over the role of the electromagnetic ether, at least inasmuch as it is the abode of field energy. To questions about the microstructure of fields, Einstein gives an interesting answer:
The special theory of relativity does not compel us to deny the aether. We may assume the existence of an ether; only we must give up ascribing a definite state of motion to it, i.e., we must by abstraction take from it the last mechanical characteristic which Lorentz had still left it. . . .(Einstein 1920, 9-10)
Think of waves on the surface of water. Here we can describe two entirely different things. Either we may follow how the undulatory surface forming the boundary between water and air alters in the course of time; or else–with the help of small floats, for instance–we can follow how the position of the individual particles of water alters in the course of time. If the existence of such floats for tracking the motion of the particles of a fluid were a fundamental impossibility in physics–if, in fact, nothing else whatever were discernible than the shape of the space occupied by the water as it varies in time, we should have no ground for the assumption that water consists of movable particles. But all the same we could characterize it as a medium.
We have something like this in the electromagnetic field. For we may picture the field to ourselves as consisting of lines of force. If we wish to interpret these lines of force to ourselves as something material in the ordinary sense, we are tempted to interpret thedynamic processes as motions of these lines of force, such that each individual line of force is tracked through the course of time. It is well known, however, that this way of regarding the electromagnetic field leads to contradictions.
Generalizing we must say this: There may be supposed to be extended physical objects to which the idea of motion cannot be applied. They may not be thought of as consisting of particles that allow themselves to be individually tracked through time. In Minkowski’s idiom this is expressed as follows: Not every extended structure in the four-dimensional world can be regarded as composed of world-threads. The special theory of relativity forbids us to assume the ether to consist of particles that can be tracked through time, but the hypothesis of the ether in itself is not in conflict with the special theory of relativity. Only we must be on our guard against ascribing a state of motion to the ether.
Savor the irony. Here is Einstein, the inventor of the photon hypothesis, arguing against modeling the electromagnetic field as being composed of distinguishable and, thus, trackable field quanta, and this because such a model is inherently non-relativistic. One easily imagines the relief Einstein felt when, prodded by Bose, he realized in 1924 that he could rescue a quantum field ontology by denying the distinguishability of quanta. Surely we see here another important reason for Einstein’s prompt and warm embrace of Bose, along with the fact that Bose’s new statistics yielded an elegant, first-principles derivation of the Planck formula for black body radiation.
Accepting Bose’s new statistics, however, meant facing up to the fact that the failure of the mutual independence of quanta outside of the Wien limit, suspected by Einstein since at least 1909, was going be a deep and pervasive feature of a still not yet established quantum mechanics. Einstein explained this point in his second paper on the extension of bosonic statistics to material particles:
Bose’s theory of radiation and my analogous theory of ideal gases have been reproved by Mr. Ehrenfest and other colleagues because in these theories the quanta or molecules are not treated as structures statistically independent of one another, without this circumstance being especially pointed out in our papers. This is entirely correct. If one treats the quanta as being statistically independent of one another in their localization, then one obtains the Wien radiation law; if one treats the gas molecules analogously, then one obtains the classical equation of state for ideal gases, even if one otherwise proceeds exactly as Bose and I have. . . . It is easy to see that, according to this way of calculating [Bose-Einstein statistics], the distribution of molecules among the cells is not treated as a statistically independent one. This is connected with the fact that the cases that are here called “complexions” would not be regarded as cases of equal probability according to the hypothesis of the independent distribution of the individual molecules among the cells Assigning different probability to these “complexions” would not then give the entropy correctly in the case of an actual statistical independence of the molecules. Thus, the formula [for the entropy] indirectly expresses a certain hypothesis about a mutual influence of the molecules–for the time being of a quite mysterious kind–which determines precisely the equal statistical probability of the cases here defined as “complexions.”(Einstein 1925, 5-6)
Einstein made the same point with equal clarity in a letter to Schrödinger in February of 1925:
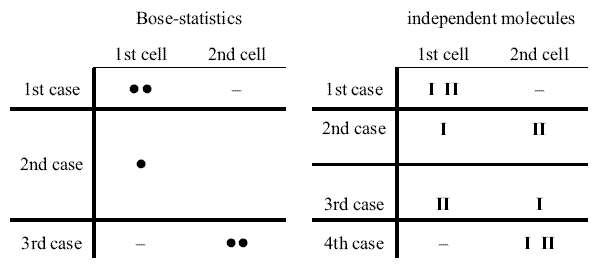
In the Bose statistics employed by me, the quanta or molecules are not treated as being independent of one another. . . . A complexion is characterized through giving the number of molecules that are present in each individual cell. The number of the complexions so defined should determine the entropy. According to this procedure, the molecules do not appear as being localized independently of one another, but rather they have a preference to sit together with another molecule in the same cell. One can easily picture this in the case of small numbers. [In particular] 2 quanta, 2 cells:(Einstein to Schrödinger, 28 February 1925, EA 22-002)
According to Bose the molecules stack together relatively more often than according to the hypothesis of the statistical independence of the molecules.
That the Schrödinger who later coined the term “entanglement” was the recipient of this letter is noteworthy, for when one reads Schrödinger’s work in developing wave mechanics over the next several months through the lens of his ongoing correspondence with Einstein, it is hard to avoid the conclusion that one of Schrödinger’s principal motivations was to find a wave-mechanical formalism capable of expressing precisely the curious failure of the mutual independence of quantum mechanical systems revealed in the new quantum statistics, just as Einstein, in 1909, deployed the metaphor of wave interference to model the failure of mutual independence outside of the Wien regime.
The key move of writing the n-particle wave function in 3n-dimensional configuration space, rather than 3-space, is necessary because only thus does one have access to a state space rich enough to comprise non-factorizable joint state functions. The price paid, famously, and much to Schrödinger’s regret, was the loss of visualizability, but that was precisely the price required by entanglement, as both Bohr and Einstein would quickly realize.
CONTINUED IN PART 2
Reprinted with permission from Iyyun: The Jerusalem Philosophical Quarterly,Volume 56, January 2007
ENDNOTES:
1. Useful histories of quantum mechanics include Jammer 1966, 1974 and Mehra and Rechenberg 1982-2001. Nothing of comparable scope or thoroughness has been attempted for relativity, but one helpful source is Kragh 1999, and much of the history of relativity can be learned from Pais 1982.
2. Some of the better literature on Bohr’s philosophy of physics includes Faye 1991, Faye and Folse 1994, and Murdoch 1987. An especially helpful source specifically on Bohr’s views on interpretation is Chevalley 1991. See also Howard 1979, 1994, and 2004, and Pais 1991,
3. Important primary and secondary sources on Einstein and philosophy include Schilpp 1949, Holton 1968, Fine 1986a, and Paty 1993. See also Pais 1982 and Howard 1990b, 1993, 2005, forthcoming.
4. Bohr 1949 and Jammer 1974, 1985 are the principal sources for this standard narrative. That the standard narrative still thrives is shown by the example of Bolles 2004.
5. For doubts about the standard narrative, see Fine 1981, Stachel 1986, Howard 1990a, and Cushing 1994.
6. Beller’s is but the culmination of a long series of works critically engaging the history of interpretations of quantum mechanics. See also Beller 1992a, 1992b, 1993, 1996a, 1996b, 1997, and Beller and Fine 1994.
7. Heisenberg’s role in creating the Copenhagen interpretation and how that view differed from Bohr’s views on interpretation are discussed in Howard 2004.
8. For a discussion of the early and enduring place of entanglement in the development of the quantum theory and in debates about its interpretation, see Howard 2006.
9. For a more detailed discussion of Einstein’s 1905 photon hypothesis paper and the subsequent history of Einstein’s worries about entanglement, see Howard 1990a.
REFERENCES:
Beller, Mara (1992a). “Schrödinger’s Dialogue with Göttingen-Copenhagen Physicists: ‘Quantum Jumps’ and ‘Realism.’” In Marcel Bitbol and Olivier Darrigol, eds. Erwin Schrödinger:Philosophy and the Birth of Quantum Mechanics. Paris: Editions Frontieres, 277-306.
——— (1992b). “The Birth of Bohr’s Complementarity – The Context and the Dialogues.” Studiesin History and Philosophy of Science 23, 147-180.
——— (1993). “Einstein and Bohr’s Rhetoric of Complementarity.” Science in Context 6, 241-255.
——— (1996a). “Rhetoric of Antirealism and the Copenhagen Spirit.” Philosophy of Science 63,183-204.
——— (1996b). “The Conceptual and the Anecdotal History of Quantum Mechanics.” Foundationsof Physics 26, 545-557.
——— (1997). “Against the Stream: Schrödinger’s Interpretation of Quantum Physics.” Studies in History and Philosophy of Science 28B, 421-432.
——— (1999). Quantum Dialogue: The Making of a Revolution. Chicago: University of Chicago Press.
Beller, Mara and Fine, Arthur (1994). “Bohr’s Response to EPR.” In Faye and Folse 1994, pp. 1-31.
Belousek, Darrin W. (1999).” Bell’s Theorem, Nonseparability, and Spacetime Individuation in Quantum Mechanics.” Philosophy of Science, 66. Supplement. Proceedings of the 1998 Biennial Meeting of the Philosophy of Science Association. Part I: Contributed Papers, S28-S46
Bohr, Niels (1928). “The Quantum Postulate and the Recent Development of Atomic Theory.”
Nature (Suppl.) 121, 580-590. Page numbers are taken from the reprinting in Atomic Theory and the Description of Nature. Cambridge: Cambridge University Press, 1934, 52-91.
——— (1935). “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Physical Review 48: 696-702.
——— (1938). “Natural Philosophy and Human Cultures.” In Comptes Rendus du Congrès International de Science, Anthropologie et Ethnologie. Copenhagen, 1938. Reprinted in Nature 143 (1939), 268-272. Page numbers are cited from the reprinting in Atomic Physics and Human Knowledge. New York: John Wiley&Sons; London: Chapman&Hall, 1958, 23-31.
——— (1949). “Discussion with Einstein on Epistemological Problems in Atomic Physics.” In Schilpp 1949, 199-241.
——— (1984). Collected Works, E. Rüdinger, ed. Vol. 5, The Emergence of Quantum Mechanics (Mainly 1924-1926), Klaus Stolzenburg, ed., Amsterdam: North-Holland.
——— (1985). Collected Works, Erik Rüdinger, ed. Vol. 6, Foundations of Quantum Physics I (1926-1932), Jürgen Kalckar, ed., Amsterdam: North-Holland.
Bolles, Edmund Blair (2004). Einstein Defiant: Genius versus Genius in the Quantum Revolution. Washington, DC: Joseph Henry Press.
Born, Max, ed. (1969). Albert Einstein–Hedwig und Max Born. Briefwechsel 1916-1955. Munich: Nymphenburger.
Bothe, Walther (1926). “Über die Kopplung zwischen elementaren Strahlungsvorgängen.” Zeitschrift für Physik 37, 547-567.
Bothe, Walther, and Geiger, Hans. (1924). “Ein Weg zur experimentellen Nachprüfung der Theorie von Bohr, Kramers und Slater.” Zeitschrift für Physik, 26, 44.
——— (1925). “Experimentelles zur Theorie von Bohr, Kramers und Slater.” Die
Naturwissenschaften 13, 440-441.
Bose, Satyendra Nath (1924). “Plancks Gesetz und Lichtquantenhypothese.” Zeitschrift für Physik 26, 178-181.
Chevalley, Catherine (1991). “Introduction: Le dessin et la couleur.” In Niels Bohr. Physique atomique et connaissance humaine. Edmond Bauer and Roland Omnès, trans., Catherine Chevalley, ed. Paris: Gallimard, 17-140.
Compton, Arthur H., and Simon, A. W. (1925a). “Measurements of ß-rays Associated with Scattered X-rays.” Physical Review 25, 306-313.
——— (1925b). “Directed Quanta of Scattered X-rays.” Physical Review 26, 289-299.
Cushing, James T. (1994). Quantum Mechanics: Historical Contingency and the Copenhagen Hegemony. Chicago: University of Chicago Press.
Davisson, Clinton, and Germer, Lester (1927). “Diffraction of Electrons by a Crystal of Nickel.” Physical Review 30, 705–740.
Einstein, Albert (1905). “Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt.” Annalen der Physik 17, 132-148. Reprinted in Einstein 1989, 150-169.
——— (1920). Äther und Relativitätstheorie. Rede gehalten am 5. Mai 1920 and der Reichs-Universität zu Leiden. Berlin: Julius Springer. Reprinted in Einstein 2002, 305-323.
——— (1925). “Quantentheorie des einatomigen idealen Gases. Zweite Abhandlung.” Preussische Akademie der Wissenschaften. Physikalisch-mathematische Klasse. Sitzungsberichte (1925), 3-14.
——— (1927a). “Bestimmt Schrödinger’s Wellenmechanik die Bewegung eines Systems
vollständig oder nur im Sinne der Statistik?” Prussian Academy of Sciences, 5 May 1927.
“Nachtrag zur Korrektur.” (EA 2-100)
——— (1927b). Contribution to “Discussion générale des idées émises.” In Solvay 1927, 253-254; quoted from English translation in Bohr 1985, 101-103.
——— (1948). “Quanten-Mechanik und Wirklichkeit.” Dialectica 2, 320-324.
——— (1949). “Remarks Concerning the Essays Brought together in this Co-operative Volume.” In Schilpp 1949, pp. 665-688.
——— (1989). The Collected Papers of Albert Einstein. Vol. 2, The Swiss Years: Writings, 1900-1909. John Stachel, et al., eds. Princeton, New Jersey: Princeton University Press.
——— (1993). The Collected Papers of Albert Einstein. Vol. 5, The Swiss Years: Correspondence,1902-1914. Martin Klein, et al., eds. Princeton, New Jersey: Princeton University Press.
——— (2002). The Collected Papers of Albert Einstein. Vol. 7, The Berlin Years: Writings, 1918-1921. Michel Janssen, et al., eds. Princeton, New Jersey: Princeton University Press.
Einstein, Albert; Podolsky, Boris; and Rosen, Nathan (1935). “Can Quantum-Mechanical
Description of Physical Reality Be Considered Complete?” Physical Review 47, 777-780.
Faye, Jan (1991). Niels Bohr: His Heritage and Legacy. An Anti-Realist View of Quantum Mechanics. Dordrecht: Kluwer.
Faye, Jan and Folse, Henry, eds. (1994). Niels Bohr and Contemporary Philosophy. Dordrecht:Kluwer.
Fine, Arthur (1981). “Einstein’s Critique of Quantum Theory: The Roots and Significance of EPR.” In After Einstein: Proceedings of the Einstein Centennial Celebration at Memphis State University, 14-16 March 1979. Peter Barker and Cecil G. Shugart, eds. Memphis, Tennessee:
——— (1986a). “Einstein’s Realism.” In Fine 1986b, pp. 86-111.
——— (1986b). The Shaky Game: Einstein, Realism, and the Quantum Theory. Chicago: University of Chicago Press.
Halvorson, Hans (2004). “Complementarity of Representations in Quantum Mechanics.” Studies in History and Philosophy of Modern Physics 35, 45-56.
Heisenberg, Werner (1927). “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik.” Zeitschrift für Physik 43, 172-198.
Holton, Gerald (1968). “Mach, Einstein, and the Search for Reality.” Daedalus 97: 636-673. Reprinted in Thematic Origins of Scientific Thought: Kepler to Einstein. Cambridge,Massachusetts: Harvard University Press, 1973, 219-259.
Howard, Don (1979). Complementarity and Ontology: Niels Bohr and the Problem of Scientific Realism in Quantum Physics. Dissertation. Boston University.
——— (1985). “Einstein on Locality and Separability.” Studies in History and Philosophy of Science 16, 171-201.
——— (1990a). “‘Nicht sein kann was nicht sein darf,’ or the Prehistory of EPR, 1909-1935: Einstein’s Early Worries about the Quantum Mechanics of Composite Systems.” In Sixty-two Years of Uncertainty: Historical, Philosophical, and Physical Inquiries into the Foundations of Quantum Mechanics. Arthur I. Miller, ed. New York: Plenum Press, 61-111.
——— (1990b). “Einstein and Duhem.” In Pierre Duhem: Historian and Philosopher of Science. Proceedings of the Conference at Virginia Polytechnic Institute and State University, Blacksburg, Virginia, 16-18 March 1989. Roger Ariew and Peter Barker, eds. Synthese 83 (1990), 363-384.
——— (1993). “Was Einstein Really a Realist?” Perspectives on Science: Historical, Philosophical,Social 1, 204-251.
——— (1994). “What Makes a Classical Concept Classical? Toward a Reconstruction of Niels Bohr’s Philosophy of Physics.” In Faye and Folse 1994, 201-229.
——— (1997). “Spacetime and Separability: Problems of Identity and Individuation in Fundamental Physics.” In Potentiality, Entanglement, and Passion-at-a-distance: Quantum Mechanical Essays in Honor of Abner Shimony, vol. 2. Robert S. Cohen, Michael Horne, and John Stachel, eds. Boston: Kluwer, 113-141.
——— (2004). “Who Invented the Copenhagen Interpretation? A Study in Mythology.” PSA 2002. Part II, Symposium Papers. Proceedings of the 2002 Biennial Meeting of the Philosophy of Science Association, Milwaukee, Wisconsin, November 7-9, 2002. A special issue of Philosophy of Science 71 (2004): 669-682.
——— (2005). “Albert Einstein as a Philosopher of Science.” Physics Today 58, no. 11 (2005), 34-40.
——— (2006). “The Early History of Quantum Entanglement: 1905-1935.” Lecture given at the conference on “Quantum Information and Entanglement,” Boston University, 24 March 2006.
——— (Forthcoming). “Einstein and the Philosophy of Science.” In the Cambridge Companion to Einstein. Michel Janssen and Christoph Lehner, eds. New York: Cambridge University Press.Jammer, Max (1966). The Conceptual Development of Quantum Mechanics. New York:McGraw-Hill.
——— (1974). The Philosophy of Quantum Mechanics: The Interpretations of Quantum Mechanics in Historical Perspective. New York: John Wiley&Sons.
——— (1985). “The EPR Problem in Its Historical Context.” In Symposium on the Foundations of Modern Physics: 50 Years of the Einstein-Podolsky-Rosen Gedankenexperiment, Pekka Lahti and Peter Mittelstaedt, eds. Singapore: World Scientific, 129-149.
Körner, Stephan, ed. (1957). Observation and Interpretation: A Symposium of Philosophers and Physicists. New York: Academic; London: Butterworths.
Kragh, Helge (1999). Quantum Generations: A History of Physics in the Twentieth Century. Princeton, NJ: Princeton University Press.
Mehra, Jagdish and Rechenberg, Helmut (1982-2001). The Historical Development of Quantum Theory. New York: Springer.
Murdoch, Dugald (1987). Niels Bohr’s Philosophy of Physics. New York: Cambridge University Press.
Pais, Abraham (1982). ‘Subtle is the Lord . . .’: The Science and the Life of Albert Einstein. Oxford: Clarendon Press; New York: Oxford University Press.
——— (1991). Niels Bohr’s Times, In Physics, Philosophy, and Polity. Oxford: Clarendon.
Paty, Michel (1993). Einstein Philosophe: La Physique comme philosophie practique. Paris: Presses Universitaires de France.
Pauli, Wolfgang (1985). Wissenschaftlicher Briefwechsel mit Bohr, Einstein, Heisenberg u.a. Vol. 2, 1930-1939. Karl von Meyenn, ed. Berlin: Springer.
Ramsauer, Carl (1920). “Über den Wirkungsquerschnitt der Gasmoleküle gegenüber langsamen Elektronen.” Physikalische Zeitschrift 21, 576-578.
——— (1921a). “Über den Wirkungsquerschnitt der Gasmoleküle gegenüber langsamen Elektronen.” Annalen der Physik 64, 513-540.
——— (1921b). “Über den Wirkungsquerschnitt der Edelgase gegenüber langsamen Elektronen.” Physikalische Zeitschrift 22, 613-615.
Rosenfeld, Leon (1957). “Misunderstandings about the Foundations of Quantum Theory,” in Körner 1957, 41-45.
Schilpp, Paul Arthur, ed. (1949). Albert Einstein: Philosopher-Scientist. Evanston, IL: The Library of Living Philosophers.
Schrödinger, Erwin (1935a). “Die gegenwärtige Situation in der Quantenmechanik.” DieNaturwissenschaften 23, 807-812, 824-828, 844-849.
——— (1935b). “Discussion of Probability Relations Between Separated Systems.” Proceedings of the Cambridge Philosophical Society 31, 555-562
.——— (1936). “Probability Relations Between Separated Systems.” Proceedings of the Cambridge Philosophical Society 32, 446-452.
Solvay (1927). Électrons et photons: Rapports et discussions du cinquième conseil de physique tenu a Bruxells du 24 au 29 Octobre 1927. Paris: Gauthier-Villars, 1928.
Stachel, John (1986). “Einstein and the Quantum: Fifty Years of Struggle.” In From Quarks to Quasars: Philosophical Problems of Modern Physics. Robert G. Colodny, ed. Pittsburgh: University of Pittsburgh Press, 349-385.
Wolfke, Mieczyslaw (1914). “Antwort auf die Bemerkung Herrn Krutkows zu meiner Note: ‘Welche Strahlungsformel folgt aus den Annahme der Lichtatome?’” Physikalische Zeitschrift 15, 463-464.





Comments