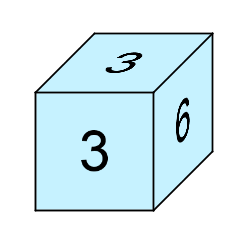
Die P has the numbers 3, 3, 3, 3, 3, 6.
Die Q has the numbers 2, 2, 2, 5, 5, 5.
The game itself is very simple: whoever rolls the highest total wins a sweet from the candy box. If the box becomes empty, the winner can take one from the other player’s pile.
Alice has the following plan. Firstly, she lets Bill select which die he wants to play with. If Bill selects die Q then Alice gets die P and they can play. However, if Bill selects die P, then Alice will get out another pair of dice and give Bill two dice P and Alice will play with two dice Q.
Is Alice playing fair?
If they each play with 3 dice of the same kind, which is the best set to have?
Is it possible to construct a die R that can beat both P and Q and still have a mean of 3.5?



Comments