This is a fairly new problem, being traced back to as recently as 2003. However, it also has the kind of counter-intuitive solution that has made it a favourite on mathematical websites and forums. In its various retellings, it sometimes suffers from a lack of stringent conditions that result in rather imaginative solutions; perfectly legitimate solutions within the parameters set but not always the ‘classic’ one. If you’ve seen this before, then speed-read to the end where we take the side of the jailer!
The problem
When I was a kid, I would happily play around with both words and numbers – I still do. Both have their aesthetic appeal. Whether it is constructing and deconstructing mathematical puzzles or
cryptic crosswords, they appear as small artefacts that reveal a grander architecture. Combine this with the serendipity of the internet, and Pi Day was just a hop, skip and jump away from Richard Feynman and pilish poetry.
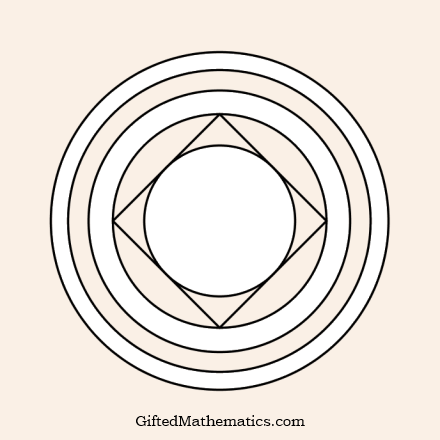
The diagram below shows five concentric circles constructed in such a way that the area of each annulus is equal to that of the central circle. Within the first annulus, a square has been constructed such that none of the points on the square lie outside the inner or outer radii of that ring.
For the first annulus, A(1), with radii r(1) and r(2), n=4 is the minimum value of n such that a regular n-gon lies wholly within or on the boundary of A(1).
Find the smallest value of n, such that a regular n-gon will not fall outside the annulus A(m) bounded by r(m) and r(m+1) for values of m = 2, 3 and 4.
Also, what is the smallest value of n for A(50)?
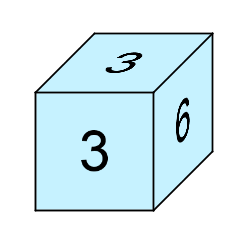
Alice wants to play a game with Bill. She has just bought some new and rather strange dice. The average of each die is 3.5, just like a normal playing die, but the numbers on each face have an unfamiliar distribution.
Die P has the numbers 3, 3, 3, 3, 3, 6.
Die Q has the numbers 2, 2, 2, 5, 5, 5.
The game itself is very simple: whoever rolls the highest total wins a sweet from the candy box. If the box becomes empty, the winner can take one from the other player’s pile.
Let N be a non-zero natural number composed of n digits. Let us then both prepend and append the number 4 to create two new numbers, 4N and N4, that are both (n+1) digits long. For example, if N is 123, then we create two numbers: 4123 and 1234.
The question is to find the smallest value of N, such that the following equation holds true:
4N = 4*N4
Again, using the example above, this would require that 4123 = 4*1234. This is obviously not true, so N=123 is not a solution.
So, find the smallest value of N and its length n.
If that was too easy, can we generalise the problem? Let K be our single-digit number, between 1 and 9 inclusive, such that KN = K*NK has a solution number N.
The "
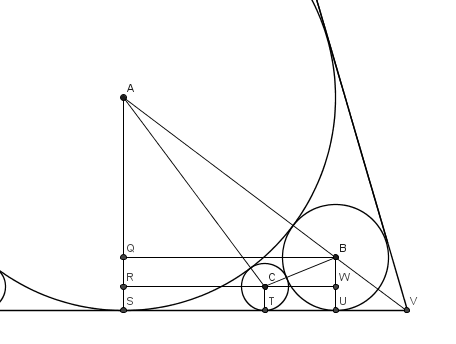
Circles Stuck in a Triangle" problem I posted last week had a rather surprising solution to it. So much so that I had to rewrite the question so that text and diagrams made sense! So here is a complete solution to what ended up being
two problems; similar but different.
The solution has three steps: firstly, we need to find the relationship between the three radii; then there is a bit of number theory to find explicit numbers for
a and
b; and finally, some trigonometry to calculate the area of the large triangle.
The c=4 case
A Tribute To Richard Feynman: Feynman Point Pilish Poems 2013
The Math-e-Monday Puzzle: Squares from a Tetrahedral Die
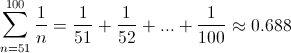Solution to The Jailer's Revenge
