Preamble over, here's your "started for 10".
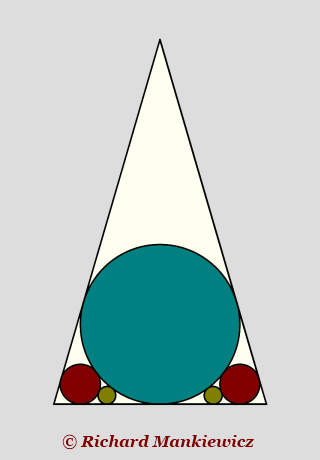
The diagram shows five circles, each with integer radius, all touching the base of the large triangle. The four smaller circles all touch their two neighbouring circles, with the large circle touching all four. The two sides of the triangle each touch two of the circles.
Let the radii of the circles be a, b and c, such that a > b > c.
Given that c has a length of 4 units, find the area of the large triangle. You may leave it as an exact solution.
Supplementary Question
Using the relationship between a, b and c, found in the first question, we can set the value of c to any square number and this will generate values for a and b.
However, if we set c=9 the triangle that encloses the circles flips over. The horizontal line used to construct the circles is now no longer the base of the whole triangle. We can redefine the triangle: the two equal sides are still the tangents of circles A and B, but the base is now the horizontal tangent to A so that the triangle still encloses the five circles.
What are the values of a and b for c=9 and why does the triangle flip over?
What happens for higher values of c, such as c=16, 25, 36 and so on?
Do the areas of the sequence of triangles generated by setting c as a sequence of squares tend towards a fixed vaue, or continue to increase indefinitely?

Full solution will be posted when a new question is published. There are, already, solutions below.
Update 7 March: have edited the above question for clarity and to include the extension problems discussed in the comments. Thanks to all participants.
11 March: a solution has now been published.





Comments