Richard Mankiewicz, our man in Bangkok, also known as Red Man (see his profile – no no, not because of Bangkok’s red light district - that would be Stickman, not Red Man!) has started a Math Puzzle Column on Science2.0, first entry: Circles Stuck in a Triangle.
Richard has another webpage where he proved to be able to come up with a lot more puzzles, so if we encourage him, he may well do a darn good job here, too - so go there and encourage him.
He asks … , well go over there and have a look already. Here is my solution, but I only tell you hints about how to get it:
Consider that the circles touch the base of the triangle, thus the heights a, b, and c (he demands a > b > c) all go straight up (right angles) from the base of the outer triangle to the circle’s centers. Circles are everywhere tangential to their radius, therefore, when two circles touch, the radius of one circle, say a, is on the same line as that of the touching one, say b, so they make a longer line, here a + b. This gives a bunch of right triangles to play with (Next picture provided by Derek Potter; below I used Mathematica5 for the images):

The Pythagoras theorem applied to the red triangle is
(a + b)2 = (a - b)2 + [x + y]2
where x and y are lengths (both parallel to the base of the triangle whose area is asked) of another two such triangles (blue and green in Derek's picture), thus resulting in
(a + b)2 = (a - b)2 + [2 (b*c)0.5 + 2 (a*c)0.5 ]2
Red Man wants integer numbers, but there are square roots(!). Thus, the integers should be already squares. The first case would be c = 1 (= 1*1), which leaves b = 4 (= 2*2), which makes also a = b*c = 4, and a triangle cannot be had (or it would have infinite area):
![]()
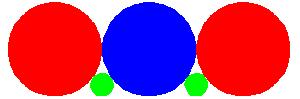
The second case is c = 4, so b = 9, which makes a = b*c = 36:

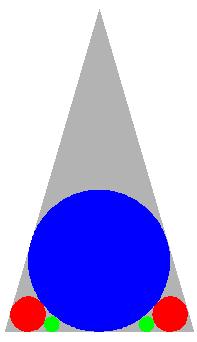
But Richard explicitly demands the next case, namely c = 9. This leaves b = 16, and thus a = b*c = 144:


Now again, an outer triangle cannot be had (if it's base is to still touch all three circles), or in other words, the “triangle’s” area would be infinite, because it opens up instead of having a top.
Don’t agree? Well maybe I am just trolling. Always think for yourself! Look at the links below for more Didactic Challenges.
-------------------
Update: Red Man does in fact not quite agree, because that all circles touch the base of the triangle was not really a strict requirement, and so he would not have to be red-faced now (which is of course no longer an option for Red Man):
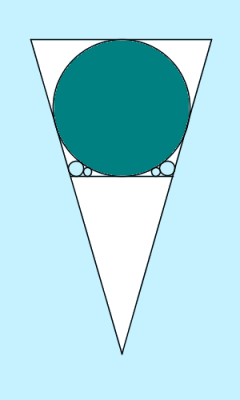





Comments