The solution has three steps: firstly, we need to find the relationship between the three radii; then there is a bit of number theory to find explicit numbers for a and b; and finally, some trigonometry to calculate the area of the large triangle.
The c=4 case
I will firstly find the general equation that links a, b and c. This will help us in the second part.
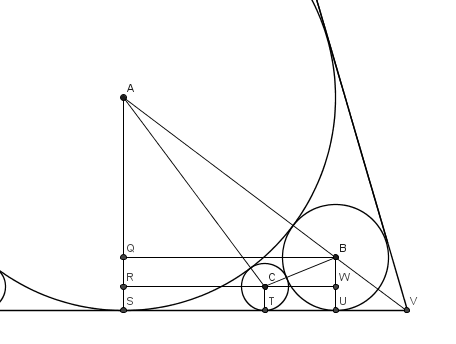
From the diagram, we have linked together the three centres of the circles to create three right-angles triangles. Our aim is to use the relationship
SU = ST + TU
Taking the large triangle AQB first, SU=QB and
AB2 = AQ2 + QB2
(a + b)2 = (a - b)2 + QB2
Similarly for triangle ARC,
(a + c)2 = (a – c)2 + RC2
And for triangle BWC,
(b + c)2 = (b – c)2 + WC2
And then we use QB = RC + WC to get
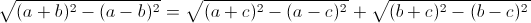
Now, this may look like an utter mess, but it simplifies rather nicely to
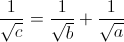
Going back to this particular question, we were first ask to solve this for c=4, giving us that the left-hand side of the equation equals one half.
We are now on the topic of unit fractions. There is only one way in which a half can be split into two unit fractions, namely, one-third and one-sixth, making b=9 and a=36.
As we now have our three radii, we can proceed with some trigonometry to find the area of the large triangle. There are undoubtedly different ways to do this, but I’m just going to go through how I did it.
If we extend the line AB it will bisect the angle at V. This angle AVS is the same as angle ABQ. And we can see that sin(ABQ) = (36-9)/(36+9) = 27/45 = 3/5. It is best to leave it this way as we don’t explicitly need the angle.
Now that we have this angle, the technique is to calculate SV, which is half the base, and then the height of the whole triangle, SX. The area will then be equal to SV.SX.
Taking the triangle ASV, we have tan(AVS)=AS/SV. As tan(AVS)=tan(ABQ)= 3/4 and AS=36, then SV=36/(3/4)= 48.
To find SX we use the triangle SXV and the relationship tan(2.XVS)=SX/SV. Here we need the so-called ‘double angle formula’ for the tangent function, and this yields the result tan(AVS)=24/7. Notice that, yet again, we have an integral Pythagorean triangle!
And finally (almost!), SX=SVx24/7 = 48x24/7 = 1152/7.
So the area of the large triangle enclosing the circles is Area=SXxSV=48x1152/7 = 55296/7.
So our final solutions are that for c=4, b=9 and a=36 and Area=55296/7.
The c=9 case
Now, one might think (as I naively thought) that if we increase the size of c, then obviously the sizes of b and a will also increase and that the enclosing triangle will get steeper and steeper. However, this is not what happens!
If we set c=9, the unit fraction formula has, again, a unique solution: 1/3 = 1/4 + 1/12. This makes b=16 and a=144. This makes the sin(ABQ)=(144-16)/(144+16)=128/160=4/5, and hence tan(ABQ)=tan(AVS)=4/3 >1. If the tangent is greater than unity then that angle is greater than 45 degrees and hence the double angle XVS will be greater than 90 degrees. This means our constructed triangle cannot meet at point X! The diagram for c=4 is wrong for c=9.
So I reconstructed the diagram for c=9 so that the two equal sides are still tangent to both circles A and B, but the horizontal ‘base’ is now a tangent above circle A, rather than being below it.
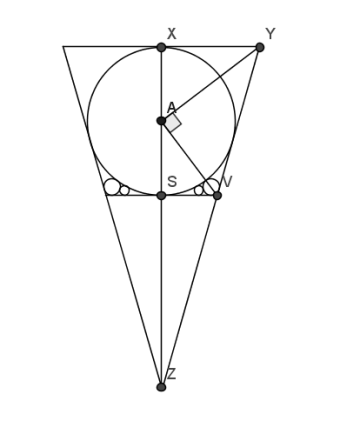
Now, with a bit of trigonometry, we find that as tan(AVS)=4/3 then tan(AYX)=3/4 and tan(VYX)=tan(2.AYX)=24/7.
With these values, we can calculate that length XY=192 and XZ=4608/7. So, finally, the area of this triangle is XY.XZ=884736/7.
It is now possible to construct any problem with c=n2 (n>1 and integral). Then b=(n+1)2 and a=(n(n+1))2. Then angle AVS is such that sin(AVS)=(a-b)/(a+b) and tan(AVS)=(a-b)/2sqrt(ab). Notice that angle tan(AVS)>1 if a/b + b/a > 6. This was false when c=4 but true for c=9, and will be true for c=n2, where n>2.
I thought such a lengthy solution merited a separate blog post.
Next Math-e-Monday Puzzle coming up...





Comments