The only place where rock solid 'proof' exists is in mathematics, which some people think is science. Yet even in mathematics there are disputes and one of them has long been Pi - or π, if you prefer. That's right, someone once may have insisted we teach the controversy about Pi, which is a delightful sort of irony.
We think of that Pi = 3 thing as a joke but it was once believed by some, even though even a moment of thought would know it's inaccurate. The reason some believed it is ...
And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it about.( I Kings 7, 23 )
That's in the spec for the temple of Solomon and, if you read that right, they are saying Pi = 3. So at least religious people who want to dispute the blending of the factual and the miraculous are staying on message. If the Bible is literal, π really does have to equal 3. Yet it certainly does not.
Why did they use that number then? Well, it was as good as any to them and they probably did a measurement. The idea that the ratio of the circumference to the diameter of a circle is constant has been around for so long that no one really knows who first said it, but that doesn't mean a number is easy to agree on.
Check out this nifty Rhind Papyrus, circa 1650 BC.

They say π is 4 X (8/9)2 = 3.16. Not bad, actually. Archimedes was a brilliant thinker in many ways and because of that he refused to even pick a number, choosing instead to use an inequality:
And he was right (1).
But that didn't mean others would not try. Al-Khwarizmi of Baghdad,who generously lent his name to the word 'algorithm' (and part of the title of one of his books, al jabr, to our term 'algebra') said the number was 3.1416 but the first real progress in figuring out Pi was in the 17th century, credited to either Leibniz or James Gregory and then it became a matter of putting in the time. A lot of time.
Pi, you see, like faith, is irrational. Also like faith, that doesn't make it bad, it just means there are places it belongs and places it does not.
And you shouldn't let your desire to make the irrational understandable get the better of you.
To wit, in 1901, a gentleman named Lazzerini tried to get a value for Pi using Buffon's needle , basically a Monte Carlo statistical method for calculating Pi(2). He made 34080 tosses of the old needle and got
yes, managing to get the same value as Chinese mathematician Zu Chongzhi circa 500 AD. How so? Well, 34080 is an strange number so he probably picked the right time to stop throwing. That works pretty well, it turned out, and Lazzerini was debunked. Even in math, you can cheat a little.
With all of the controversy surrounding Pi, you'd think a bureaucrat would step in to settle it once and for all, right? That's what bureaucrats do, after all. Well, one did. In 1897 the Indiana state House of Representatives proposed their new mathematical truth:
Be it enacted by the General Assembly of the State of Indiana: It has been found that a circular area is to the square on a line equal to the quadrant of the circumference, as the area of an equilateral rectangle is to the square of one side. (Section I, House Bill No. 246, 1897)
Unfortunately, it never came to pass. That would have given us a reason to make fun of Indiana. Instead we'll have to stick with ridiculing cajuns for making up their own science.
TRIVIA
Want to know your birthday in Pi? Go here.
Who first used the symbol π for the ratio?
Welsh mathematician William Jones wrote "3.14159 andc. = π" in 1706. When Euler, he of the famous equation that makes planes fly (even if you think it's Bernoulli) adapted it, it became popular.
Want to remember Pi better?
Here is a nifty mnemonic. The number of letters in each word corresponds to the successive number in Pi.
"How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard"
translates to
3.14159265358979323846264
***************************************************************
NOTES:
(1) His thinking, courtesy of Cambridge:
Consider a circle of radius 1, in which we inscribe a regular polygon of 3 X 2n-1 sides, with semiperimeter bn, and superscribe a regular polygon of 3 X 2n-1 sides, with semiperimeter an.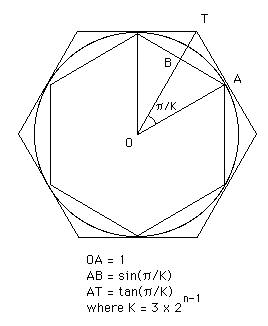
The diagram for the case n = 2 is above.
The effect of this procedure is to define an increasing sequence
b1 , b2 , b3 , ...
and a decreasing sequence
a1 , a2 , a3 , ...
such that both sequences have limit π. Using trigonometrical notation, we see that the two semiperimeters are given by
an = K tan(π/K), bn = K sin(π/K), where K = 3 X 2n-1. Equally, we have
an+1 = 2K tan(π/2K), bn+1 = 2K sin(π/2K), and it is not a difficult exercise in trigonometry to show that
(1/an + 1/bn) = 2/an+1 . . . (1)
an+1bn = (bn+1)2 . . . (2)
Archimedes, starting from a1 = 3 tan(π/3) = 3√3 and b1 = 3 sin(π/3) = 3√3/2, calculated a2 using (1), then b2 using (2), then a3 using (1), then b3 using (2), and so on until he had calculated a6 and b6. His conclusion was that
b6 < π < a6 .
It is important to realise that the use of trigonometry here is unhistorical: Archimedes did not have the advantage of an algebraic and trigonometrical notation and had to derive (1) and (2) by purely geometrical means. Moreover he did not even have the advantage of our decimal notation for numbers, so that the calculation of a6 and b6 from (1) and (2) was by no means a trivial task. So it was a pretty stupendous feat both of imagination and of calculation and the wonder is not that he stopped with polygons of 96 sides, but that he went so far.
**********
(2) Suppose you have a tabletop with a number of parallel lines drawn on it, which are equally spaced (say the spacing is 1 inch, for example). Suppose you also have a pin or needle, which is also an inch long. If you drop the needle on the table, you will find that one of two things happens: (1) The needle crosses or touches one of the lines, or (2) the needle crosses no lines. The idea now is to keep dropping this needle over and over on the table, and to record the statistics. Namely, we want to keep track of both the total number of times that the needle is randomly dropped on the table (call this N), and the number of times that it crosses a line (call this C). If you keep dropping the needle, eventually you will find that the number 2N/C approaches the value of pi!
REFERENCES:
"History topic: A history of Pi", by J J O'Connor and E F Robertson August 2001, Cambridge
"Pi has a long and interesting history!" University of Arkansas at Little Rock
"A Brief History of π", Exploratorium.edu




Comments