He has taken the sweatpants off and is now trying to put them back on inside out without removing the ankle cuffs.
Yes, it can be done.
Holly Bernstein, who earned a PhD in mathematics at Washington University in St. Louis in 1999, watches him struggle for a bit and then says, “Remember the pants have more than one hole. You don’t necessarily have to put them back on the way you put them on in the first place.”
Having dropped that intriguing hint, she moves on to the next group of kids, who are trying to detach a pencil threaded with a loop of string that passes through the buttonhole of a shirt and through itself as well, attaching the pencil to the shirt.
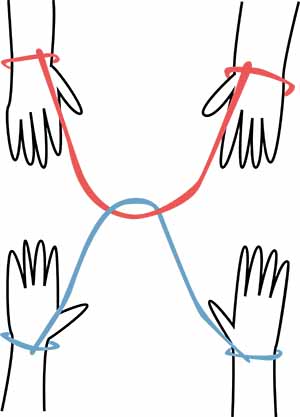
Your hands are tied and the rope is entwined with a partner’s rope. Can you disentangle the ropes without cutting or untying them? Click here for answer. Credit: Simin
“This one looks easy,” Bernstein says encouragingly, “but it is actually hard. The puzzle was made for an insurance company to use a gimmick to sell life insurance," she said. The agent fixed the pencil to a customer’s buttonhole and then bet that he or she couldn’t get it off. Customers who failed had to buy an insurance policy. It looks so easy many people took the bet — and lost.
To which academic discipline do giant sweatpants and pencils-tied-to-shirts belong?
The answer is topology, a branch of mathematics that is sometimes called rubber-sheet geometry. Topologists imagine objects as made of rubber and then stretch, twist, dent or otherwise deform them, noticing which of the objects’ properties survive theses deformat

In topology, a coffee cup is equivalent to a doughnut. Because both objects have one hole, one can be deformed in such a way that it turns into the other. Wikipedia
Bernstein had brought a dozen different topological puzzles — each a variation on turning coffee cups into doughnuts — to this Sunday’s meeting of Washington University’s math circle, setting them up on tables throughout the room. At one station the kids had to manipulate interlocked handcuffs so that they fell apart; at another they were challenged to tie a knot in a string without letting go of either end; at a third they tried to cut a hole in an index card large enough to fit their bodies through.
It’s hard to imagine more kid-friendly activities and the kids buzzed from puzzle to puzzle like so many fruit flies on ripe bananas. Blake Thornton, PhD, who has led the Washington University math circle for the past nine years, moved from group to group, trying a puzzle here, redirecting a kid there, often smiling at overheard comments.
Math circles, which bring together professional mathematicians and young students, have been a part of mathematical culture in Russia since the 1930s and in Bulgaria for nearly a century.
Mathematicians disturbed by the poor quality and low level of math education in this country started a math circle at Harvard University in 1994. The University of California at Berkeley followed suit in 1998 and now has more than 400 participants. Washington University's math circle was founded in 2002 by then-math department chair Stephen G. Krantz.

The snack for this meeting of math circle? Strange donuts, of course, from the St. Louis donought shop of the same name. This is the bloody eyeball donut. Credit: WUSTL
“Every week I recruit a professional mathematician,” Thornton said, “and the presenters come up with a fun mathematical activity, generally a new and original activity that they themselves are interested in. We have a large number of presenters and the kids get something different every week.”
It is the participation of practicing mathematicians that gives the math circle its special character. School math is mostly symbol and number manipulation that has no obvious point, said Thornton, who is the coordinator of lower division teaching in the mathematics department. Too often in school math is taught by someone who considers it drudgery, an attitude that proves contagious.
The math circles give kids a chance to find out what mathematics is really like and to get to know mathematicians as people as well as experts, Thornton says.
“Because practicing mathematicians understand the larger context of puzzles or problems, we can adjust them for each student,” Thornton said, “allowing them to make progress instead of leaving them in a state of bafflement and frustration.”
“We come up with an activity that’s fun, and math that scales so that it works for ninth-graders as well as third-graders. If we can scale it like that, most of the kids stay interested the whole time because they’re busy making progress on hard problems,” he said. “We try to celebrate progress. Most kids don’t get to the ultimate solution. But we make progress on the way and they can see that progress and they’re excited by it.”
“Some parents tell me,” he added, “that their child’s week pivots around math circle and they would be devastated if they couldn’t come.”
Source: Diana Lutz, Washington University in St. Louis






Comments