Two days ago I offered you three problems in experimental particle physics, of varied complexity. Three readers tried answering the test in the comments thread: a rather underwhelming turnaround, but what did I expect - we are deep in Christmas vacations after all.

I will give below my own answers to the questions, and then comment some of those I received. For ease of reading, I paste here again the three questions.

1. The charged pion is a particle made by a  pair of quarks: for the positive one we have the composition , and for its antiparticle . The charged pion decays in about ten nanoseconds into a muon and its neutrino, as in .
In the decay, the quark-antiquark pair "annihilate" into a negative W boson, which then materializes the muon-antineutrino pair. The question is: why does the pion prefer to decay to a muon-antineutrino pair instead than in an electron-antineutrino pair ? Note, weak interactions, which are responsible for the decay, are flavor-democratic: there is a thing called "lepton universality of the weak currents" which demands that the intensity of the couplings to all leptons be the same. Also note, the pion has a mass of 139 MeV, the muon a mass of 105 MeV, the electron a mass of 0.5 MeV, and the neutrino is virtually massless. How come the pion prefers the heavier muon, if there would be more "phase space" to yield an electron instead ? 
Hint: helicity is the key. Okay, you don't know what helicity is, so go to wikipedia, damn it.

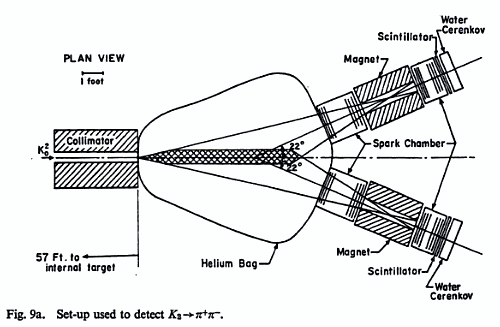
2. In the famous 1964 experiment that demonstrated the violation of CP invariance and won Cronin and Fitch their Nobel prize in Physics, the four experimenters (Christenson, Cronin, Fitch, and Turlay) allowed a beam of neutral kaons to decay inside a large bag
filled with Helium. The observation of the decay of two charged pions of the neutral kaons constituted indisputable proof of the fact that these particles had violated the combined symmetry of charge-conjugation and parity. In fact, the beam of kaons had been
treated in a way that only one of the two possible quantum states had survived.
The question is, why Helium ? What properties has this gas that were suitable for the experiment ? Mind you, this is a tricky one.
Hint: the answer has only in part something to do with Physics...

3. You have a b-tagging algorithm which is capable of properly identifying jets as being originated from b-quark hadronization. You measure two numbers: the probability
P(btag|bjet)=0.5 as the probability of tagging a jet if it was originated by b-quark hadronization; and the probability P(btag|not bjet)=0.01 of incorrectly btagging a non-b-jet. From those, you then get P(no-btag|bjet) = 1-P(btag|bjet), and similarly P(no-btag|no-bjet) = 1-P(btag|no-bjet).
The question is: given a sample of 1000 jets tagged as b-jets by the algorithm, what fraction of them are b-jets ? In other words, what is P(bjet|btag) ?
Hint: think Bayesian!

My answers:

1. The charged pion is a spin-zero particle which needs to decay into two fermions -there is only neutrinos, electrons, and muons available with a smaller mass, and they are all fermions. Fermions in the standard model are left-handed: they carry a half unit of spin, and when we say "left-handed" we mean that their spin has direction aligned opposite to their momentum vector. Further, the anti-particle of a left-handed fermion will have to be right-handed, i.e. its spin will have to be aligned along the momentum.
Now, only massless fermions need to be perfectly left-handed: for a massive particle, helicity is not a good quantum number because the massive particle travels at a speed smaller than the speed of light: for an observer who traveled faster and overtook it, the spin of the fermion would flip its direction! For this reason, the less relativistic a fermion is, the less strict is its obedience of left-handedness. Weak interactions, in a way, are increasingly willing to waive the rule, the slower the fermion is traveling.
Now, in the pion rest frame, it is clear that one of the two fermions will have to get a half-unit of spin aligned in a direction opposite to that of its own liking. Take a negative pion decaying into a lepton-antineutrino pair: the antineutrino will be forced to be right-handed, and will have the spin pointing along its direction of flight; the other particle, which travels away in the opposite direction, will then have to also be right-handed, to balance to zero the total spin of the final state. A right-handed electron is thus much more unlikely than a right-handed muon, because it is emitted with a much higher velocity, being less massive. This is the cause of the strong suppression factor that makes pions decay primarily into muon-antineutrino pairs.

2. What the experimenters tried to minimize with the large helium bag was the regeneration of neutral kaons with the wrong CP eigenstate. Regeneration is a phenomenon that occurs when a quantum system which is the superposition of states gets scrambled up by the different interactions that its constituents undergo. A perfect example of this phenomenon happens when the long-lived component of neutral kaons traverses matter, because weak interactions act differently on the and  quark doublets of which long-lived neutral kaons are made. Let me explain this in some more detail. The physics of neutral kaons is absolutely fascinating!

Neutral kaons are made by a combination of quarks; their antiparticles are instead a combination. These two states "mix together", and what we observe to decay is a short-lived component, called , which may decay into a pair, and a long-lived component, which decays into pion triplets ( ), with a lifetime 600 times longer. It turns out that the long-lived component is in a quantum state of CP = -1, and so it cannot decay to two pions, a state of CP= +1. We can write the short- and long-lived components as a superposition of and :


The Nobel winners created a beam of neutral kaons and allowed it to drift in vacuum until the short-lived, two-pion-decaying component had died away completely. They then studied the decays of these pure  particles: observing the forbidden two-pion decay would be proof of CP violation -unless a few  had popped out in the beam by a regeneration in matter!

The regeneration phenomenon "remixes", in a way, the soup of K0 and anti-K0 which make up the : by suppressing more the anti-K0 component (which may produce hyperons when colliding with nucleons) the quantum state acquires a small component of K0_S, spoiling the experiment! Check it out below:

1. The beam is made purely by


2. Matter reduces differently the K0 and anti-K0 components: ,


3. The new quantum state can be written or more properly as


4. If, as we stated, f1 and f2 are different (and they are, due to the willingness of the s-quark in anti-K0 to bind with a (ud) pair from a nucleon to create a (uds) combination, something which anti-s quarks cannot do when interacting with ordinary matter) the interaction of with matter regenerates a non-zero component!

The Nobel winners were very careful to minimize the impurity of the beam of kaons, such that the observation of the two-pion decay would be a true smoking gun of the CP violating interaction.  Now, the best choice to avoid the regeneration phenomenon would of course be a large vacuum vessel, but that was impractical to handle and consequently costly. Hydrogen, being the lightest element, was the next-best choice, but the explosive properties of the substance made it very dangerous to deal with in the experimental setup. So Helium was the best compromise. Below you can see a sketch of the experimental setup: the beam of kaons enters from the left between the two collimators, and the detectors "observe" the region within the Helium bag.



3. This was a tricky question, but the hint was there as a warning: if one really applied Bayesian reasoning, one would have started asking oneself the right question straight away: what is the prior probability of the examined jets to be originated by b-quark hadronization in the sample ? In other words, what is P(bjet) before anybody pulls out a b-tagging device ?
If one knows that number, one can determine the fraction of b-tag jets that are true b-jets in the sample; if one doesn't, there is no solution.
In fact, Bayes theorem provides the solution fairly quickly if we know P(bjet). Let us take P(bjet) to be 0.05, which is not too different from what typically happens at a hadron collider. In that case we can use Bayes formula:

P(bjet|btag)=P(btag|bjet)*P(bjet)/P(btag).

Notice that at the denominator we have P(btag). This can be computed from the data at hand: from a generic sample of jets, 5% of which are b-jets, the probability to b-tag one of them is

P(bjet)*P(btag|bjet)+(1-P(bjet))*P(btag|nobjet),

which turns out to be 0.05*0.5*0.95*0.01=0.0345. This means that in a sample which has 5% of true b-jets, our 50% efficient, 1% fake rate algorithm will tag a total of 3.45% of them.

Now we have all the data we need: We use Bayes formula to get

P(bjet|btag)=P(btag|bjet)*P(bjet)/P(btag) = 0.5*0.025/0.0345 = 0.724.

In a sample of 1000 b-tagged jets, we might thus expect that 724 of them are true b-jets.
Now that we have worked through the example above, which fixed P(bjet) at 5%, it is immediately clear why the data in the original problem was insufficient: we had no "prior" to use as an input. The answer is: "There is not enough information to determine the fraction of b-jets in the 1000 b-tagged sample."

Now that I in turn did my own homework -that is, writing down the solution in a sort-of-understandable fashion- let me have my share of fun. I will comment the answers given by the few courageous readers who took the challenge:

Lubos Motl:
1) Correct, if a bit too long. But I do like long answers, they show the true reasoning of  the student and allow for a better evaluation.
2) Wrong! Lubos said the reason for Helium was to minimize interactions with the pions, i.e. the final state of the decay. The answer, as I discussed at length above, was to avoid the regeneration phenomenon as much as possible.
3) Correct, although Lubos is very cautious ("I think the dependence on P(bjet) does not disappear"). He correctly explains how the result depends on the prior.
Result: 2/3.

SLW:
1) not quoted
2) Partly correct! The cost factor is in fact the driving reason for choosing a Helium bag.
3) I did not check the formula, but I suppose that not reaching a definite value means that SLW did realize it was not solvable. So I would give two-thirds of a point for this answer.
Result: 1.4/3.

Tulpoeid:
1) Basically correct, although not discussed in enough detail.
2) Wrong! Tulpoeid is also misled by the decay rather than by the nature of the phenomenon to be constrained.
3) Correct, although living on the shoulders of the previous solver.
Result: 1.5/3.

This was fun. I will have more questions for the second half of the vacations!