Among the few really interesting pieces of subatomic physics that are being pursued at the Tevatron, the search for flavor-changing neutral-current (FCNC) decays of neutral B mesons is probably the cleanest, most clear-cut one. I have reported about it in the past, but here I wish to give an introductory-level account of the matter. I will insert a few footnotes here and there to specify points where I have been voluntarily imprecise for the sake of clarity.
Introduction: Where have all the K-zeroes gone ?
The crucial role of the physics of neutral-current decays of neutral mesons is not an invention of recent years. In fact, the hypothesis of the existence of a fourth quark, the charm, traces back to precisely the observed effect of an absence of neutral current decays of the lighter brothers of B0 mesons, the K0 particles. The K0 mesons were not observed to decay into pairs of muons, a process which had all reasons to occur, possibly with the intervention of a neutral Z boson, or by a less exotic double-W exchange. The story is worth telling, although probably I myself have done so already a dozen times in this column. Just in case you missed it.
In the sixties, only charged-current weak interactions were known to exist. In truth, an obscure 1967 paper by Weinberg and Salam (who would later win a Nobel prize for that) had hypothesized the existence of a neutral Z current to fit together with charged W+ and W- weak vector bosons in a SU(2) triplet. However, not many in the field of theoretical physics, let alone you and me, had really taken that hypothesis seriously. And the absence of a Z boson would not solve the problem of a non-observation of dimuon decays of K0 mesons.
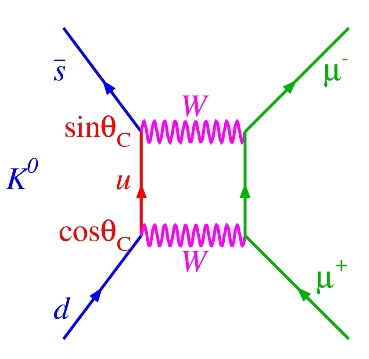In fact, it is not just by the exchange of a so-far-unknown Z boson that K0 mesons might be thought to produce a muon pair. One could imagine that the process took place via box diagrams, with the exchange of two W bosons, as shown in the figure on the right, where time is to be understood as flowing from left to right, and where the two quarks in the K0 are shown with blue lines: a K0 meson is a bound state of a If one computed the rate at which K0 meson decays should produce dimuon pairs via box diagrams, one obtained a large value, and yet those decays just were not there. It was unconceivable to miss such a clean signature: tweaking Oscar Wilde, one might say that missing one muon in a carefully crafted detector would be a tragedy, but missing two would start to smell of negligence.
So, were had all the Kzeroes gone ? They had decayed to other final states, sure. But the absence of the "natural" dimuon decay was a puzzle, regardless of the existence or not of Z bosons, let alone the capability of Z bosons of turning a quark flavor into another (which, incidentally, had to be possible if the strange-quark had no partner). Why was the box diagram not contributing ? A never failing law of quantum physics says that everything that is not forbidden is compulsory. There was a law to discover then, one forbidding the dimuon decay.
This puzzle was not very long-lived: Glashow, Iliopoulos, and Maiani (GIM) in 1970 found a way to force the dimuon decay of neutral kaons down to unobservably small levels. They hypothesized the existence of a fourth quark, the charm, with electrical charge equal to that of the up-quark: a partner of the "single" strange quark, creating a tidy scheme of two quark doublets to complement the two doublets of leptons, the electron-electron neutrino and muon-muon neutrino pairs.
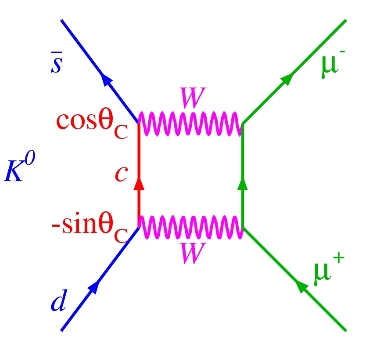The reasoning of GIM was as follows: If the s-quark could turn either into a up-quark or into another quark, call it a charm-quark, there would then be two Feynman diagrams to add together in order to compute the rate of the unobserved dimuon decays. To the first diagram shown above, a second one needs to be added, as shown on the right. And it turned out that the two diagrams interfered destructively! They almost exactly annihilated each other just like vodka and lemon juice in a carefully crafted cocktail. With a fourth quark of mass of about 1.5 GeV, Glashow and his collaborators could explain away the anomalous non-observation of such a striking, simple-to-detect final state of neutral kaons. The law was a deep one: Let there be quarks, but only in pairs! 
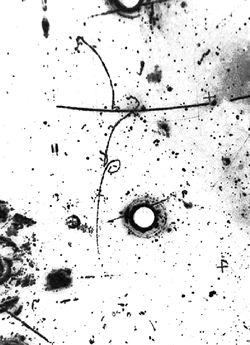As we know, the charm quark was discovered in 1974, during what was later called "the November revolution": a few weeks that changed everybody's mind on the reality of quarks. The GIM creature was a true entity! And, just one year before, physicists had cheered the discovery of weak neutral currents at the Gargamelle bubble chamber, through collisions of a muon neutrino beam with electrons. The picture on the left is of historical significance: it is a one-in-seven-hundred-thousand pictures, which shows a energetic electron (the wiggly track starting at the bottom) bouncing off its original haven inside an atom, apparently recoiling against nothing. That nothing is a muon neutrino, which enters from below, hits the electron, and leaves unseen, remaining unaltered by the scattering process: it did not need to change its identity -its flavour- when emitting the Z boson which kicked in the balls the innocent electron seen in the picture.Since 1973 flavor-changing neutral currents have remained a Holy Grail for particle physics. If seen, at a rate different to the really small one predicted by the standard model, FCNC processes would be a wonderful smoking gun for new physics: one would be hard pressed to avoid having to insert new particles (supersymmetric, or still others) in the equations describing the physics of elementary particles.
Now, there is one last thing to note before we get back to B mesons. With neutral kaons, the rates of FCNC decays predicted both by the standard model are small, but larger than for B0 mesons. Buck for buck, new physics will sooner show up in the FCNC decays of the heavier neutral B mesons. These are governed by the same physics, except that there is a b-quark at the place of the s-quark: one may write them as (bd) instead of (sd)[1]. Actually, there are now two different neutral mesons to study, as we have noted above: (b-sbar) and (b-dbar) combinations. B0 decays to dimuon pairs are still very rare, but they are arguably a better probe of new physics.
Neutral B mesons, a laboratory for new physics searches
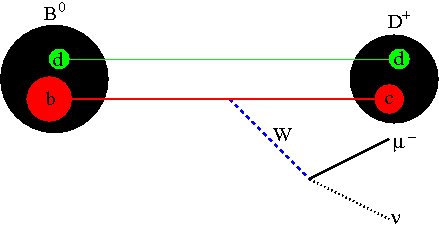Neutral B mesons -labeled "B0"- are particles made up by a b-quark tied together with a lighter d- or s-type quark[1]. These particles are predicted to decay by a so-called charged-current weak interaction, the process whereby a heavy quark emits a virtual W boson, becoming a different lighter quark (a charm in the figure). Instead, the emission of a quantum of neutral weak currents, a Z boson, is not capable of changing the flavor of the quark, and thus does not contribute to the decay[2]. The picture on the right should clarify this concept: if we substitute a Z for the W, the red quark line remains a b-quark, because the Z is incapable of turning it into a lighter one. Not having any energy to take away from the unmodified b-quark, the Z cannot be emitted.As often happens in physics, when something is predicted to be exactly equal to zero, or excessively small, it becomes a very advantageous thing to measure. Given that the standard model predicts a less than one-in-a-billion rate, the
When you observe two muons, the quite natural thing to do is to combine their energy and momentum measurements to find what is the "invariant mass" of the object which disintegrated into them[3]. CDF and D0 have been searching for two decades for the signature of muon pairs yielding the mass of the B0 meson[3]. With the large datasets now available, these searches are getting close to be sensitive to the "one-in-a-billion" standard model expectations, and in so doing they are excluding chunks of parameter space for new physics models (such as the already mentioned ones generically labeled Supersymmetry) which instead predict a larger fraction of B0 mesons materializing a
The present status of limits to dimuon decays of neutral B mesons
So let us see where the Tevatron experiments are in the exciting search for these rare decays.
The most recent result by CDF is based on a dataset obtained by skimming through about 300 trillion proton-antiproton collisions[4]. The search involves the use of a Neural Network -a software model of a brain, if you will- to select the events which most resemble the expected features of neutral B meson decays to dimuon pairs.
The Neural Network is trained to recognize the events most likely to resemble a true dimuon decay of B0 particles, using a simulation of that process; shown both signal and background events, the artificial brain learns to tell them apart. When then the machine is shown real data, it gives a response (the "NN output") between 0.0 (not a likely signal event at all) and 1.0 (an event really indistinguishable from a true signal). A selection of events with NN output close to 1.0 thus preferentially selects signal-like candidates. The reconstructed dimuon mass distribution of these candidates is finally studied to put a limit on the number of events that may be attributed to B decays. Below you can see such a distribution, which indeed shows no enhancement in the two regions (limited by hatched red and blue lines) where CDF would see a bump: masses corresponding to those of B_d and B_s mesons.
From the absence of a signal, one can set a limit on the branching fraction of B0 mesons to dimuon pairs. The status of the art is best displayed in the figure below, which shows the progress of the search as a function of the integrated luminosity delivered by the Tevatron collider to CDF and D0; the lowest yellow point by CDF is the one obtained with the search discussed above.
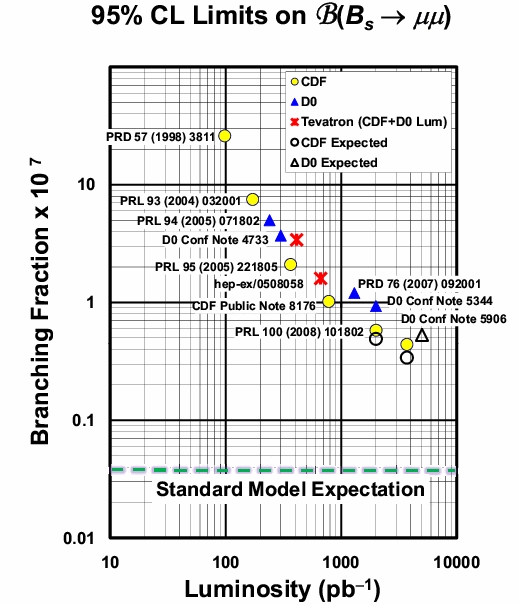
It is not difficult to realize that the two experiments will never reach the precision required to measure the standard model process, which is lying at the cyan dashed line, one full order of magnitude below present limits. The search is statistics-limited, so a factor of 10 in sensitivity demands a factor of 100 of more data -which the Tevatron will never collect. However, supersymmetric models are already being sorted out by the rate of B0 mesons which are being excluded. That, ultimately, is what makes things interesting. We are suffocating supersymmetry bit by bit, by subtracting her the breathing space. Soon, somebody will have to come up with the idea that she is not only hiding in a corner, but that she brought with her a oxygen mask!
----
[1] In truth, the B0 meson is made up by a anti-b-quark and a d-quark, or a anti-b-quark and a s-quark. Its antiparticle is instead a b-antid or b-antis combination. I have omitted discussing antiparticles above, to avoid the distraction.
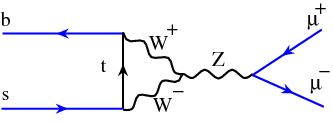[2] To give some more detail on this issue: the standard model does predict the reaction yielding muon pairs from the B0 decay; but the probability of such an event is of less than one in a billion,because one has to invoke a multiple exchange of vector bosons: for instance, a W needs to be emitted to change the b-quark into a lighter one, but then it must be re-absorbed by the quark line, and finally a Z boson can indeed materialize in a pair of muons. Another similar process is shown in the diagram above, where two W bosons fuse into a Z before the latter can produce a dimuon pair; a further one is the box diagram shown below, equivalent to the ones already shown for K0 mesons.
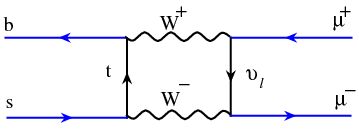Other reactions are of course possible, but they are "higher-order" in the weak coupling constant, and are thus even more impossibly rare.[3] When one combines the two muons together to reconstruct the mass of their parent, one is implicitly assuming that the two muons come from the same source, and that no other particle was emitted in the same reaction, otherwise the result will depend on the energy taken away by these additional bodies.
[4] This corresponds to the acquired four inverse femtobarns of integrated luminosity.
Comments