Carl Brannen is well known to the regulars of this blog. He is an independent researcher and my favourite non-professional theorist, because he gives me the hope that brilliant minds, who were diverted from the natural path of doing basic research, may return to it for good. And Carl provides us with another important proof: that institutionalized science does sometimes listen to the voice of those who have something to say regardless of who signs their monthly paycheck. It may give them a hard time getting their papers published, though.
Carl has recently won a honorable mention for a paper on gravitation, but he has new ideas -some good, some bad, but all intriguing- all over the board of fundamental physics. He accepted my invitation to tell us about some of his ideas on fermion generations below. Enjoy !

Isidor Rabi is famous for asking the question “Who ordered that?” in response to the discovery of the muon, a heavy version of the electron. Later another charged lepton, the tau, was discovered so now there are a total of three particles that act alike, the electron, the muon, and the tau. The other elementary particles with spin = 1/2, the quarks and neutrinos are also duplicated in three versions. Probably thinking about sex, the physicists call these versions “generations”. Among the elementary particles, only those with spin-1/2 appear in generations. Why is that? My new paper attempts to answer Rabi’s question.

Our experiments are restricted to very low energies compared to the Planck energy; perhaps spin-1/2 at much higher energies than we can experiment with behaves differently. This post gives an undergraduate level introduction to a paper that proposes this as an explanation for the generations. We will begin by discussing classical measurements of position and spin, and then move on to the quantum case.

Measuring a beam of bullets

Consider the dual-barrel Vulcord Semi-Gatling gun. This is a two-barreled high speed rifle. It’s unique in that the two barrels have opposite barrel twists. Consequently, the stream of bullets produced by the gun come in two varieties, half the bullets have right handed spin and half have left handed spin. In addition, the gun has a rotational randomizing function which causes the bullets to have random offsets as they leave the gun and which randomizes the left handed and right handed bullets. So the bullet stream, call it the “bullet beam”, consists of bullets with two random characteristics, their offset position in the beam, and their spin. A drawing may assist:

Vulcord gun

For simplicity, we’re assuming that all the bullets move in parallel, and we’re only going to take into account only one position coordinate, the z-distance. So the bullets have just two characteristics, position and spin. If the gun is fired for long enough, the different offsets of the bullets leave tracks (particle tracks) that are parallel and randomly distributed. We’ll use two colors, red and green, to distinguish right and left handed bullet tracks, respectively. And for printing, we’ll make the right handed tracks dotted. A drawing of just a few tracks:

Random classical bullets from Vulcord gun

To measure the positions of the bullets in the beam, we insert a barrier that stops all but a small portion of the bullet beam. The barrier is “classical” in that it does not modify the characteristics of the bullets that get past it. Thus the effect of two barriers is the same as one:

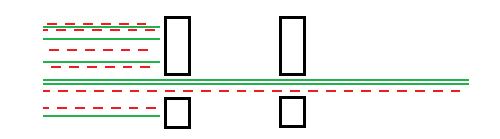
Measuring bullet positions with a barrier

We can also measure the spins of the bullets in the beam. To do this, we use a special sort of bullet sorter, a “Stern-Gerlach” sorter. It acts by deflecting the right handed bullets down, into a “beam stop”. Thus only the left handed bullets stay in the beam. And just like with classical position measurements, repeating this measurement has the same effect as doing it once:

Measuring a beam of electrons

Now we will consider a beam of electrons. We will still measure the position of an electron in a similar fashion to the classical measurement of the beam of bullets. But instead of measuring the spin of the bullet, we will measure the spin (in the z direction) of the electron. Measurements of electron spin give either +h-bar/2 or -h-bar/2 so this is in analogy to the two possible spins of the bullets.

So long as our measurements are sufficiently inaccurate, we will obtain results analogous to the classical results. That is, repeated measurements of position and spin will give unchanged results. But this changes as we increase the sharpness with which we measure position. When the slit in our position measuring block approaches the length of the de Broglie wavelength of the electrons, the electrons will be scattered by the slit. And then, repeated measurements of position no longer give the same result as a single measurement. This behavior is can be ascribed to the Heisenberg uncertainty principle. Position measurements cause changes to the electron’s behavior that alters the result of a second measurement of position:

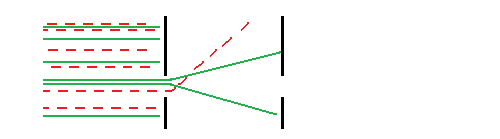
With the way this material has been introduced here, it’s natural to expect that sufficiently accurate measurements of spin should also result in modifications of the electron’s behavior in such a way as to change the result of a second measurement. That’s not how standard physics predicts but it is what is proposed in this paper: At sufficiently small time intervals, measurements of spin act like measurements of position and cause scattering.

Spin as an emergent property

To put meat on the bones of the above discussion, we have to find a way of writing the stable, long term spin in terms of the unstable, short term spin. The paper does this by using Feynman’s path integral formulation of quantum mechanics to compute propagators. Mathematically, propagators are “Green’s functions”, functions which when found, allows differential equations to be easily solved.

In the path integral formulation, we compute “probability amplitudes” between an initial state (initial condition) and a final state (condition) by considering all possible paths between the states. The initial condition might be how the experimenter prepares the particle while the final state might be a place where a particle detector looks for the particle. The paper shows how to obtain stable, long term spin path integrals in terms of the unstable, short term spin path integrals. This is done by writing the long term propagators in terms of short term propagators.

Orthogonality and Superselection Sectors

The calculation ends up with three orthogonal long term propagators. A familiar example of orthogonal states are the spin-up electron and the spin-down electron. These are the same particle but are sufficiently distinct that they are not the same state. For example, a spin-up and a spin-down electron can exist in the same state (other than spin); the Pauli exclusion principle does not require them to have orthogonal wave functions. Thus the two electrons in the ground state of the helium atom are both in 1s wave functions.

The spin-up and spin-down wave functions are a complete basis for spin-1/2. This means that we can arrange for spin in any direction by taking linear superpositions of the spin-up and spin-down states. Linear superposition does not apply to all possible wave functions in quantum mechanics. Instead, it is restricted to “superselection sectors.” An example of an illegal linear superposition would be one mixing an electron with a photon.

This sort of behavior is mirrored in the elementary particle generations; linear superpositions of different generation fermions are created in weak interactions. These mix the generations according to the experimentally determined CKM and PMNS matrices. Consequently a natural way of obtaining the generation structure of the elementary fermions is to describe the different generations as orthogonal propagators; just as with spin-up and spin-down, linear superposition is implied and therefore mixing occurs.

More Information

The concept of measurement apparatus that only allow one spin state to pass is due to Julian Schwinger, who created an elegant description of quantum mechanics now called “Schwinger’s measurement algebra”. You can buy his introduction to quantum mechanics book on Amazon, “Quantum Kinematics and Dynamics” right now at the bargain price of $39.89. Or you can read the two papers he published that describe the theory, “The Algebra of Microscopic Measurement” and the following paper, “The Geometry of Quantum States”.

An excellent non mathematical introduction to path integrals for electrons and photons is the short popular book by Richard Feynman, “QED The Strange Theory of Light and Matter” now available at Amazon for $3.98; every graduate student in physics should have this book. An introductory textbook to path integrals for elementary particle theory is “Quantum Field Theory in a Nutshell” by Anthony Zee. And a good book that discusses superselection sectors is PCT, Spin and Statistics, and all that, by Raymond F. Streater and Arthur S. Wightman.