The result is simple to state in a single sentence, although it will take me several pages to explain it acceptably. The Higgs boson is excluded at 95% confidence level in the 130-210 GeV mass range, if there are four generations of matter fields.
I can hear you thinking "Ah, here's the rub... Always some fine print." True, but although the conditional clause changes the picture significantly, I believe the result is still quite important. In fact, who said there should be three, and only three families of quarks and leptons ?
Why three ?
We needed two decades of investigations to find out that there are three families of quarks and leptons. It all started in 1974, when the second-generation charm quark was discovered at SLAC and Brookhaven; the search saw high points when a third-generation lepton was discovered at SLAC (a somewhat painful process, since the discovery took several years to be accepted as such) and when the third-generation bottom quark was discovered at Fermilab. The culmination point, and the (maybe temporary) end of the story was set when the top quark was discovered at the Tevatron collider in 1994, completing the third generation of matter fields and creating a pleasing, symmetrical picture.
In the meantime, indirect investigations at LEP determined that there are only three types of light neutrinos. Through these data, supported by some ancillary indirect evidence, we convinced ourselves that matter in the universe exists in the form of three generations of quarks and leptons.
So all known quarks and leptons, which share the property of having a half-integer spin but are otherwise quite different objects, can be arranged in a tidy scheme of three families, or generations. The first generation includes the up and down quark, together with the electron and its neutrino: these would at first sight appear to be sufficient to create the complexity of the universe around us. However, it is not so: even forgetting about the existence of antiparticles for each of those bodies, we have to come to terms that the universe would be quite different with a single generation of matter.
You might argue that as long as we do not create energetic collisions we do not need to take strange, charm, bottom, and top quarks in account, and that even muons, taus, and their neutrinos are unnecessary. You would be wrong: strange quarks might make up a significant part of the core of neutron stars; cosmic rays produce second and third generation fermions day in and day out; and even the good-old protons contained in the fat molecules making up your buttocks contain quarks of the second and third generation of matter. You would be sitting on a different kind of ass if the proton was only made of up and down quarks!
So there are three generations. Why not four, or five, or an infinite replica then ? Well, there are both theoretical arguments and experimental constraints that tend to let us think that three is indeed the magical number upon which Nature (the bitch, not the magazine) has apparently decided to base the construction of our universe.
But theoretical predictions are always leaky, and experimental constraints can be circumvented. So indeed, one should take a "know-nothing" stand here, and be prepared to be surprised. Indeed, the CDF collaboration has found last year a nagging excess of a fourth-generation-like object with mass in the 450-GeV region, in a search performed by CDF colleagues, among them my five-times colleague John Conway (we are both members of the CDF and CMS collaborations; we are both members of the CDF Spokespersons Publication Review Group; we are both members of the CMS Statistics Committee; and we are fellow bloggers, too!).
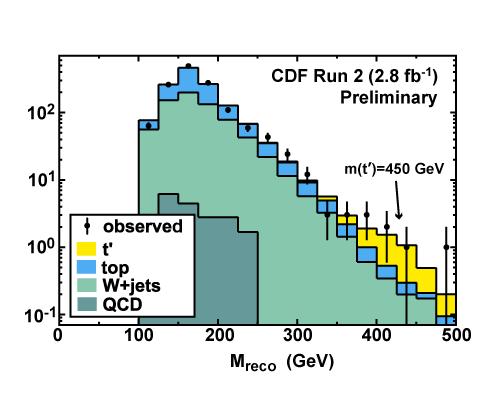
The figure above is the culprit: a few events appear to be compatible with the production of "top-prime" objects of 450 GeV mass. This is a two-sigma-like excess, and it is probably bound to be reabsorbed once more data will be added to the search; however, for the moment it is an interesting would-be signal, one to keep an eye on.
Four generations and the Higgs boson
While direct searches for additional fermions are underway, indirect searches are also progressing. A fourth generation of quarks and leptons would have a significant impact in several pieces of known standard model physics: virtual loops involving these additional particles could produce changes in branching ratios, modify couplings, and affect the rate of production of several subatomic processes.
Higgs boson physics is not surprisingly one sector where one expects a large impact from additional quarks: the Higgs talks to all massive particles regardless of whether they are fermions or bosons, charged or neutral, green or blue. Indeed, a heavy quark changes the branching ratios significantly from the default picture: this can be seen from the figure below.
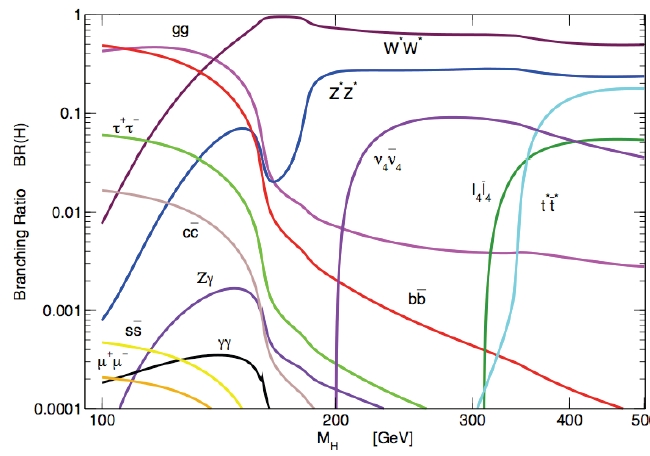
This is an incredibly busy plot. Yet rather than busy I would call it "information-rich". It contains a huge amount of information on Higgs boson physics, and it would require me a series of postings to explain all of its features. Let me describe the salient points though.
On the horizontal axis you find the unknown, hypothetical mass of the Higgs. On the vertical axisyou may read off the probability that one such particle will decay in a given final state. The different curves show exactly what is the probability of a decay into one of the possible final states, as a function of Higgs mass. Now, at "low" mass (say, below 120 GeV), the regular standard model Higgs would mostly decay to a b-antib quark pair (red curve) -the heaviest pair of fermions available. But here, with the increased chance of a quark loop, the gluon-gluon decay (dark pink curve) becomes dominant.
At higher mass, instead, little changes: the preferred decay mode is the one involving a pair of W bosons. However, as you increase the Higgs mass further -say above 200 GeV in the graph above-, the possibility arises that you produce two fourth-generation objects: these decays "turn on" at Higgs masses equal to twice the new fermion mass. To compute the figure, the theorists had to assign hypothetical masses to all the fourth-generation fermions, and their guess was as good as yours would have been; so they chose values just slightly higher than the exclusion limits for each of the new fermions.
Besides the presence of high-mass channels opening up, the reason why the probability of Higgs decay into one state or the other changes even at low mass if there is an additional pair of heavy quarks is that these quarks couple strongly with the Higgs boson (since the coupling is proportional to the mass of the particle), and thus the Higgs is likely to "split" into a pair of such virtual quarks. The latter cannot materialize as they are, though, because this would violate energy conservation: to be produced they require an energy larger than half the Higgs mass. Therefore they rejoin by closing a virtual loop. Before they do, however, they may emit all the available energy in the form of a pair of W or Z bosons, or two gluons. This suppresses the decay to fermions, while the gluon-pair final state gets a large increase.
So the modification in the decay pattern is bad news for experimentalists! Gluon pairs are as rare as a rainy day in London. But this is not the end of the story... Invert the arrow of time in the process above, and you will also immediately realize how a fourth quark strongly increases the cross section of Higgs production. Let me explain why.
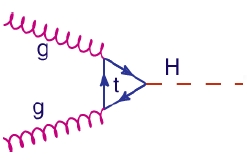At a hadron collider the Higgs is most readily produced from a pair of gluons. But the Higgs does not "couple" directly to the gluons (gluons have no mass). The production occurs via the creation of a quark loop, like the triangle shown in the graph on the right. Any quark may run in the loop, but the top quark dominates the proceedings, because quarks couple to the Higgs boson proportionally to their mass squared, and the square of the top quark mass is ten thousand times larger than that of the next-in-line, the bottom quark.Now, with a pair of fourth-generation massive quarks available for the virtual loop, the process becomes significantly more frequent: the cross section of Higgs production increases by a full order of magnitude! The contribution of the new quarks, if these are much more massive than the Higgs, is independent on their mass, because the rarity of the virtual loop is perfectly countered by the increased Higgs-new quark coupling. You can see that in the figure below.
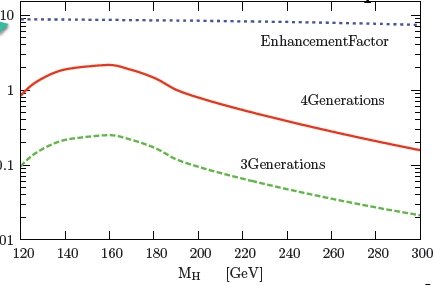
The rate of Higgs bosons (ignore the units on the vertical axis) produced at the Tevatron is plotted here as a function of the Higgs mass, for the case of three fermion generations and four fermion generations. The enhancement, shown by the dashed line on top, is almost a factor of ten!
But We See No Higgs...
Let us take stock. We have seen that a fourth quark would make the Higgs more likely to decay to gluon pairs in a wide range of masses. We have also seen that the production rate would increase tenfold. But we know that the rate of Higgs production cannot be large, lest we would have seen it already at the Tevatron! What gives ?
It gives an exclusion. One may take the predicted yield of W boson pairs from Higgs production in the four-generations scenario, and compare with the maximum number of such decays that may be hidden in the CDF and DZERO data without having been spotted. If the former exceeds the latter, the model is excluded. Since the whole thing depends on the unknown mass of the Higgs boson, but it does not depend on the mass of the hypothetical fourth-generation quark, we get a simple plot with the Higgs mass on the horizontal axis: the one below.
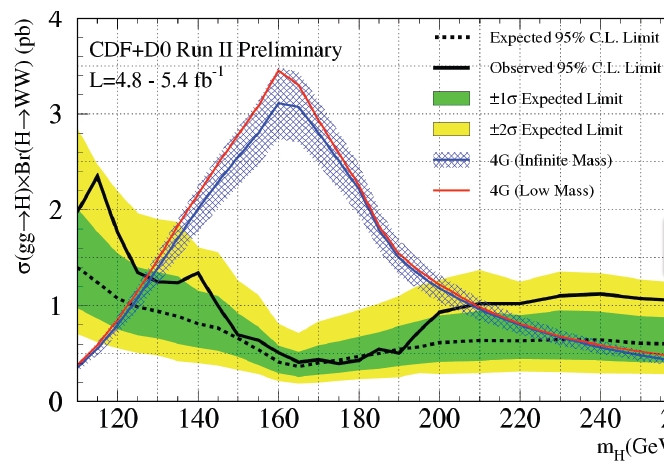
Here you may appreciate just how much would a tenfold cross section increase in cross section do: the Tevatron would have unmistakably seen such a thing! Indeed, a broad range of excluded Higgs boson masses is derived by taking the region where the excluded cross section (black line) lays below the blue one: from 130 to 210 GeV. These are the Higgs mass values where the limit is below the expected cross section.
Also note that the cross-section of Higgs production, once multiplied by the branching fraction to W boson pairs, "peaks" at about 160 GeV: of course: the branching fraction to WW pairs is highest there. Finally, please take note of a fact: the blue and red curves, representing the predicted cross sections in a 4-generation scenario with infinite 4-generation-fermion masses, or in a scenario where these have a mass just above the existing limits, are almost coincident.
Of course, I have made things easier than they are in the few paragraphs above: the search for this Higgs in the "four-generation" scenario has been re-optimized in order to take into account several nuisances. But the general picture is what matters.
Concluding remarks
I think the result I have described above is quite interesting. We give too much importance to the Higgs in the scenario where there is nothing else around; we also give a lot of stress to searches for supersymmetric Higgs bosons, when we really have to guess the value of dozens of parameters in order to pick a SUSY scenario; change these, and everything changes. I get dizzy when I think at the number of caveats and distinguos necessary to fully appreciate a SUSY Higgs search.
Instead, here you get a real limit from a standard model scenario which just sees the addition of another generation of matter fields. Beware, the actual value of the mass of these new, yet-to-be-found objects does not affect much the limit on the Higgs mass. This is the most interesting thing in the whole analysis: bring the fourth-generation fermion masses to infinity, and nothing changes. Amazing!
Further reading
If you are serious about this, you may take advantage from the documents you will find in the public page of the Higgs group in CDF.
I also recommend my own discussion of the search for a fourth-generation quark by CDF.
A discussion of the latest Tevatron limit on the standard model Higgs boson (with three generation of matter fields assumed) is here.
Four things about four generations are discussed in this post.
Comments