In the last few days I indulged in a rather technical description of the checks I made on DZERO's evaluation of the significance of their observation of Omega_b particles. In those occasions I did not discuss either what the Omega_b is, nor what is its relevance, nor the details of how DZERO collected a small but significant sample of events characterized by the production of that ephemeral particle.

I wish to fill that gap today, and I hope I will be able to keep the discussion at a level which enables anybody who is interested in particle physics to follow it. In so doing, I will probably try to simplify things a little, at the expense of some accuracy. Never mind: this is no scientific publication, and the most important thing is clarity. What matters is that you, dear reader, give me feedback on whether the discussion was too cryptic for you, or acceptable. The exercise for me consists in setting the bar high enough that it is not too easy to jump it, but low enough that it will not stop you from trying. Help me adjusting its height by telling me your level of studies and your understanding of the text below, in the comments section!

Three sexy red quarks

Ok. So what is the Omega_b, and why should you care about it ? To answer this question in a proper way, let me first discuss the discovery of an ancestor of the Omega_b, the Omega baryon. It was a revelation of great importance to physicists in the sixties.

"What do you get if you put together three sexy red quarks ?" "Dunno, but just thinkin' of that I'm getting a haDR-on! "

Jokes aside, hadrons are composed of triplets of quarks (combinations called baryons) or quark-antiquark pairs (which are called mesons). The quarks are held together by the strong force, which is sensitive to an attribute of quarks called "color" -conventionally described as red, green, or blue for quarks; antired, antigreen, or antiblue for antiquarks. Contrarily to the joke above, however, you cannot put together quarks of the same color: only colorless combinations -id est ones where the three colors blend in together (creating baryons), or when a single color is counterbalanced by its anti-charge (and you get the mesons).

What keeps together hadrons was not known in the sixties, when quarks were merely a means of explaining the different properties of known hadrons, and were not yet considered real physical objects. If one took quarks seriously, however, one would then have to accept a whole set of intriguing conclusions.

Among the fourscore or so hadrons thus far known, in 1964 nine baryons with similar properties had been discovered and classified, by placing them at the vertices of a structure called "decuplet". The structure was the result of hypothesizing that baryons were made of triplets of quarks of three different kinds -up, down, and strange; and that they possessed an attribute called "spin", which could take only two opposite values -plus a half, or minus a half. Three quarks with perfectly aligned spins would make a total spin of 3/2: those nine baryons shared in fact exactly that peculiarity.

If you studied physics, you would soon learn that the symmetry properties of a system usually tell you a lot about its structure. With particles this is a crucial concept. However, to study symmetries, you need to learn group theory, which is not a common item in your typical list of "99 things to do before I die". Since I am well aware of that (while you, dear reader, do not care to come and realize the stunning beauty that hides behind the crazy math of group theory), let me be synthetic.

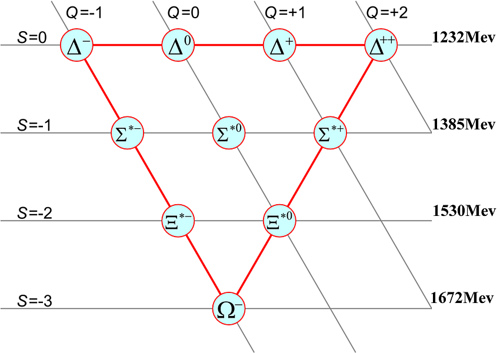Group theory teaches you how to classify different triplets of three different objects with some kind of weird mathematics: 3x3x3 = 10+8+8+1. The decuplet "10" contains totally symmetric arrangements of the three quarks: in particular, these combinations have the spin of the three quarks aligned in the same direction (spin, which takes on two values only, is also subject to its own symmetry, but let us not defocus here). By arranging the observed baryons at the vertices of the triangular structure shown on the right, one could explain them as different arrangements of the three quarks, sharing many properties: a symmetry -a common quality of the resulting baryons, meaning that a member of the decuplet could take the place of another in particle reactions without making much difference.

Let us see how this worked: in the upper row the four states labeled "Delta" had a quark composition (ddd), (ddu), (duu), and (uuu): one went from a total charge of -1 (because each down-type quark has an electric charge of -1/3), a state labeled Delta-, all the way to the Delta++, the sum of three up-quarks, of charge +2/3 * 3 = +2. On the second row, one had to substitute a d-quark for an s-one: (sdd), (sdu), (suu). These were the Sigma baryons. On the third row lie the Xi baryons, which contained a second s-type quark: (ssd), (ssu). One could only guess that the bottom of the pyramid would contain a triply-strange baryon. It was called Omega (sss).

The decuplet structure was not a meaningless construct at all: one could observe that by going down from Delta to Sigma states, the baryon mass increased by about 150 MeV: the Particle Properties Data Book tells us in fact that Delta states all have a mass of 1232 MeV. On the second row, the three spin-3/2 Sigmas lie at 1387.2 MeV, 1383.7 MeV, and 1382.8 MeV respectively. On the third row, the Xi states have masses of 1535.0 MeV and 1531.8 MeV. It was quite hard for physicists not to guess that a new baryon was awaiting to be discovered, with a quark composition (sss), a mass in the 1680 MeV ballpark, and a spin equal to 3/2. Its true mass is now known to be 1672.45 MeV.

Oh, and I have yet to say anything about the decays. It turns out that one could often observe strange baryons to decay by changing one of their s-quarks into a lighter u-quark. This, in fact, was the peculiarity of "strange" matter: it was readily produced in hadronic collisions -a sign that the interaction producing them was strong- but it took a long time to decay -a sign that the interaction disintegrating them was weak! That was due to the fact that strong interactions could create two strange particles together -one containing a strange quark, the other containing an anti-strange one. The total strangeness of the system was zero, and strong interactions could do that -no strangeness in, no total strangeness out. However, when one strange particle decayed, this implied a change of strangeness, and only weak interactions could do that, only much more slowly!

What to expect for the triply-strange Omega baryons, then ? Of course! A three-vertex chain (or four, including the Omega creation point). Because of some details that it would not be trivial to explain, the Omega would typically decay after traveling about one inch to a Xi^0 pi^- pair, (a second "vertex", after the production one); the neutral Xi baryon then would travel for three more inches and turn into a Lambda- neutral pion pair (third vertex), and the Lambda would finally lose its last strange quark by turning into a proton and a negative pion (fourth vertex!), after traveling some further three inches. Physicists had access to everything they wanted to know about the Omega before discovering it, if they believed in the quark model of hadrons!

Those were the years when a single event would make a discovery. And one single event made it in 1964, because the tracks left by charged particles crossing the pressurized vapor of a bubble chamber exposed to streams of protons could not be mistaken! Below you can see the original plate which fruited the Omega discovery to a team led by Nicholas Samios at the Brookhaven National Laboratory. They used an 80-inch bubble chamber to take the picture shown below:


(left: the actual picture of tracks in the bubble chamber; right: interpretation in terms of particle trajectories).

The overpressurized gas of the chamber was exposed to a stream of negative kaons -mesons made by a strange and an anti-up quark. The kaon, hitting the proton, materialized two additional strange-antistrange quark pairs; the anti-strange quarks made two new kaons, a k-zero and a K-plus, while the three s-quarks left behind made a Omega particle. After a brief path, the Omega produced a Xi^0 and a negative pion; the Xi^0 traveled further, giving rise to a Lambda-pi^0 decay; the pi-zero immediately turned into a pair of photons; the photons materialized soon into electron-positron pairs, while the Lambda made it further, finally decaying into a proton-negative pion pair.

If you ask me, the one above is among the sancta sanctorum of Physics Pictures - one of the most beautiful pictures Man has ever taken. A frame which contains strong, electromagnetic, and weak forces all summarized in a firework display of quantum mechanics at work. Simply delightful. What is more, from the curvature of all the tracks left in the bubble chamber, one can measure the mass of all the unstable bodies participating in the reaction! The mass in fact confirmed the hypothesis beautifully. In a future post I will challenge you to make the exercise of computing the Omega mass from the measured four-momenta of the tracks you see in the picture - it is material I discuss during my course of subnuclear physics. But now let us return to the Omega_b.


Back to the Omega_b

The physics of the Omega_b, a baryon much heavier than the Omega (the quark composition of the former has one b-quark in exchange for one of the strange ones of the latter) is not altogether too different from that of its lightweight cousin. Here I cannot entertain you in a discussion of the predicted properties of such a gathering of fancy quarks; suffices to say that it is rarely produced in proton-antiproton collisions, because strange and bottom quarks are not contained in the projectiles, and they have to be created together if they are to bind within a baryon. This rarity prevented it from being discovered at lower-energy accelerators. Energy does matter -the b-quark weighs 5 GeV alone, and that energy must be created by the collision- as much as does the large amount of data where this particle was sought by the DZERO and CDF collaborations, during the last few years.

Rarity of production gets multiplied by the rarity of the reaction which is chosen to provide us with a perfect reconstruction of all the involved particles, just as was the case with the lucky shot discussed above, which was worth the Omega discovery to the Brookhaven team. The studied decay of the Omega_b proceeds by the creation of a Omega - J/Psi pair, when the latter then turns into a mu^+ mu^- pair, while the Omega goes directly into a Lambda-K^- pair, the lambda then turning into a proton-pi minus pair.

Since each decay acts independently of all others, the probabilities for the quoted reactions multiply each other: the J/Psi->mu^+ mu^- decay occurs 5.93% of the time; the Omega-> Lambda K^- happens 67.8% of the time; and the Lambda->pi^- proton has a 63.9% chance. And then there is the unknown rate of the quite fancy Omega_b->Omega J/Psi decay: maybe a hundredth of a percent, as happens for the already known and measured, similar decays of Lambda_b or Xi_b baryons involving J/Psi mesons. Take everything together and you get a rate of 2.6 in a million!

The executive summary of the two paragraphs above is the following: produce a million Omega_b particles, and you will only be able to see two or three of them in that decay chain. And, to produce a Omega_b, you need a million proton-antiproton collisions! No wonder the Omega_b has remained unearthed for so long.

You might be virtually raising your hand from the back there at this point, with a meaningful question. What forces us to choose such a rare combination of decays, to observe the Omega_b ? Could we not use more frequent chains ? Well, yes. But the one discussed is our best chance, because it is fully reconstructed. What that means is that the end product of the reaction is a set of electrically charged, stable particles: a proton, a negative pion, a negative kaon, and two muons (beware, I used the term "stable" in a wide sense -pions, muons and kaons will eventually decay, but only after leaving well-measured tracks in the detector).

Noise, noise, go a-way, come a'gain ano-ther day (and possibly, in another experiment)

All the final state particles mentioned above can be measured precisely in the DZERO and CDF detectors. This allows us to determine the mass of their parent bodies -the Lambda, the J/Psi, the Omega, and the Omega_b itself. This is a crucial fact, which I need to stress here: the importance of mass measurements is not so much the chance to precisely determine the Omega_b mass, but rather, the chance it gives us to remove "noise"!

Background -also known as "noise"- is everywhere, and the success of a search for a tiny signal depends on our ability to throw it out of the window as dirty water, without getting rid of our baby signal in the meantime (please pass me this analogy, whose origin is old literature). To explain this concept, let us take the starting dataset used by CDF in its analysis: a sample of twenty-seven million reconstructed J/Psi decays into dimuon pairs, selected by a dedicated online trigger system, sifting through the three million collisions occurring every second in the core of the CDF detector. Now fast-forward to the final dataset where CDF demonstrates the presence of the Omega_b peak: 35 events, a third of which are Omega_b decays. To achieve this amazing one-in-a-million selection, cuts are made on the reconstructed mass of the Lambda from proton-pion combinations; and on the Omega mass, reconstructed by combining the Lambda momentum -previously determined from the proton-pion pairs passing the Lambda mass cut- with an accompanying measured kaon.

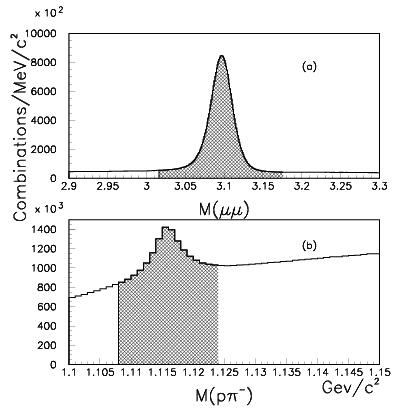The graph at the top on the right shows the first step of the selection: the glorious peak of J/Psi decays. This already entails some reduction of the dataset: only candidates in a 160-MeV-wide mass window (the shaded band) centered on the true J/Psi mass value are retained, and this allows CDF to get rid of "continuum" muon pairs not due to J/Psi decay, which have no reason to be present in real Omega_b decays. Then look at the bottom plot, which shows the Lambda peak for events already selected by the J/Psi mass window cut: again, a cut around the Lambda mass (again shown by the shaded band) reduces significantly the dataset, discarding events where a Lambda is not seen.

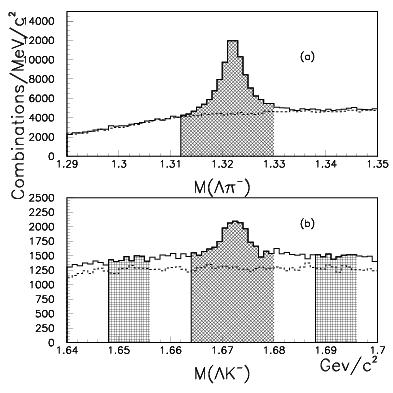The second graph, shown on the left, displays the Xi (top) and Omega (bottom) reconstruction. What does the Xi have to do with the Omega_b search, you may well ask at this point -if you remember the decay chain we are after, that is. The Xi does matter a lot: the kinematics of the Xi -> Lambda pi decay is very similar to the one of the Omega -> Lambda K, and by studying them together we learn more about the signal. (In fact, a number of additional signals are unearthed and measured by this analysis, but I prefer to avoid discussing them here, lest I lose the three of you who have made it this far deep in this article). The shaded bands again show the selection of Xi (top) and Omega (bottom) candidates, in events that have been selected to contain a J/Psi signal and a Lambda signal. Please note: from 27 million events, in the Omega window we are already down to maybe 20,000 events, and the event reduction has been achieved with a ridiculous loss of reconstructable signal events. This would never have been possible, if we had chosen to search for Omega_b decays involving non-measured neutral particles! No mass ? No party!

Tricks are not over in the fantastic analysis, for which we have to be grateful most of all to Patrick Lukens (right), the "muon guy" of the early CDF detector construction years, who also happens to be an expert in the reconstruction of rare b-physics processes. But I cannot disclose all of those tricks to you, because this post is becoming of biblical length. Rather, let me show you what happens when you combine the four-momentum of the reconstructed J/Psi candidate with the four-momentum of the Omega candidate.

Something magical indeed occurs: most of the times, the two momenta will not match well to a common vertex -a hint that their production is uncorrelated: that is, the two particles have then been produced at different space-time points during the reaction. Even when the two momenta match, anyway, the computed mass of the body which is hypothesized to have originated them in its decay is seldom ranging above 5.8 GeV -the lower bound of the search window that CDF examines, knowing from theoretical calculations that an Omega_b meson has to be slightly heavier than that.

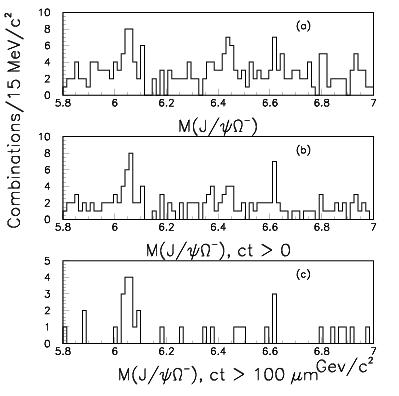Moreover, there is a final bullet to shoot: we know that the Omega_b must be a long-lived object, because its decay is governed by weak interactions -ones that change the bottom into a charm quark. So the Omega_b must travel away from the interaction point, where it has been produced. A cut on the travel path of the J/Psi - Omega system does the trick, and improves dramatically the signal to background fraction. It is this latter selection that accepts only 35 events in the 5.8-7.0 GeV mass window. The graph is shown on the bottom plot on the right: the cluster of events at 6.05 GeV is due to a handful of Omega_b candidates, magistrally selected by Pat and collaborators. Please note that although a Omega_b signal must be present in the data before selecting long decay paths (the cut labeled "ct>100 um", or 100 micrometers), the presence of backgrounds in those histograms prevents us from drawing any conclusions there.

If you have read my former posts on DZERO's Omega_b signal, you will by now know that one may cast a well-thought of objection here: the signal is not extremely significant, and it might not pass the test of "observation-level significance". The authors of the analysis estimate it at 4.9 standard deviations: just a little bit below the 5-sigma level which is necessary to have a foul-proof "observation-level" claim. By the way, in my former posts I have shown that the DZERO signal is also at 4.8-4.9 statistical deviations, much less than the value they quote in their paper, 5.4 sigma.

In order to further prove that the Omega_b is observed, CDF now performs a multi-dimensional fit to the candidates, by determining together the mass and the lifetime of each Omega_b particle. This latter fit (see left), which enlarges the selection accepting more Omega_b candidates, also introduces additional critical information, and reduces further by a factor of ten the already tiny probability that the observation was due to a background fluctuation. CDF can thus both measure both mass and lifetime of the Omega_b, but also claim a 5.5-sigma observation!

I will discuss the detail of the lifetime measurement, as well as the measurement of the ratio between the branching fraction of Omega_b -> J/Psi Omega to the one of Xi_b -> J/Psi Xi, or to the one of Lambda_b -> J/Psi Lambda decays, in another post. All those additional determinations are added icing to an already yummy cake! Instead, let me make a point on the mass measurement.

The mass of the Omega_b: a controversy about to blow up

The CDF paper, which has already been sent to a scientific paper as we speak, puts the matter very bluntly from the introduction:

[discussion of past observations of baryons containing bottom quarks precedes] "In this paper, we report the observation of an additional heavy baryon and the measurement of its mass, lifetime, and relative production rate compared to the Lambda_b production. The decay properties of this state are consistent with the weak decay of a b-baryon. We interpret our result as the observation of the Omega_b baryon (|ssb>). Observation of this baryon has been previously reported[6], however, the analysis presented here measures a mass of the Omega_b to be significantly lower than ref.[6]".

Yes, you guessed it right. Ref. [6] is the DZERO paper, which I have discussed in the two previous pieces on the Omega_b. What is the problem with the two measurements ? Well, let us compare the mass determinations:

DZERO: M = 6165+-10+-13 MeV = 6165+-16.4 MeV;
CDF:   M = 6054.4 +- 6.8 +- 0.9 MeV = 6054.4 +- 6.9 MeV.

First thing to note: the CDF measurement has an error bar 2.4 times smaller than the DZERO measurement. Second thing to note: the DZERO measurement has a systematic uncertainty which is larger than the total uncertainty of the CDF measurement. Third thing to note: the CDF measurement has virtually uninfluent systematic uncertainty -a by-product of the extremely good charged particle tracking and its perfect calibration.

Fourth, and crucial, thing to note: the two measurements differ by 110.6 MeV! If we took the CDF and DZERO quoted uncertainties at face value, we would have to conclude that the two experiments have measured two distinct particles!!! In fact, their "difference", in units of total uncertainty, is of 110.6/sqrt(16.4^2+6.9^2)= 6.2 standard deviations! In other words, it is more likely that these are two distinct particles, than each of them is simply a fluctuation of backgrounds!

How is that for a controversy ? I will leave you here, dear reader, but I will be back on this topic very soon, with pseudo-experiments again, trying to determine what is the mass of this particle, and by how mass we have to inflate the systematic uncertainties quoted by each experiment in order to make the two results be a credible outcome of the measurement of the same particle.

In the meantime, I stress one point: CDF has a 5.5-sigma observation of the Omega_b. DZERO, if we have to trust my own calculation, has a 4.8-sigma evidence for it. CDF has the better mass determination; DZERO has one which is systematically dominated, and disagreeing with CDF's by 6.2 standard deviations...