The concept origin of space-time itself as a emergent property of a collection of fundamentally quantum systems without a notion of space-time is not new. When this is done usually certain presuppositions are made about the nature of the underlying quantum system. In a recent paper posted to the arXiv by scientist out of Cal Tech develop aversion of this approach in which noting is assumed about the quantum system at the smallest scale. (Chun Jun Cao, 2016)

Starting with a collection of a large number of generic,general, Hilbert spaces they find a way to get ideas of metric, length,curvature and Einstein equations. The only reservations I personally would have about this are the same ones I have about any new theory (especially my own by the way). Specifically, new theories are by definition untested by new data. I could be missing something but nothing about this hypothesis from Chun Jun Cao, Sean M. Carroll, Spyridon Michalakis is conceptually all that far-fetched. It is especially good that they feign no hypotheses about what specific kind of quantum system would have to live inside any one of the Hilbert spaces (nor do they seem to assume it is just one kind of thing going on at that short length scale.)

I know I usually write about my own wild theories. That is true of any theorist if you really objectively look at it. Usually we only write of each other’s models to be critical of them. Instead I give you a layman’s breakdown of a model unlike anything I am working on right now which from my preliminary understanding of it seems quite plausible. Trust me from one theorist not involved in a work, especially at this early stage, “seems quite plausible” is glowing over the top praise.

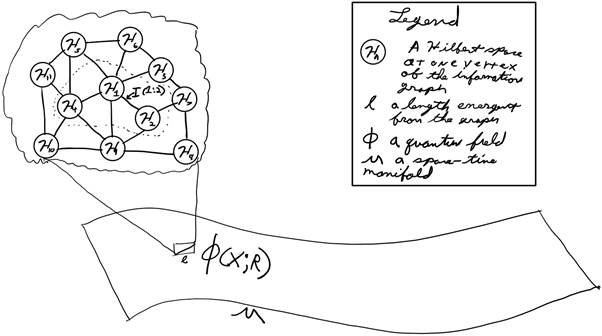Usually these spaces are associated with a particular quantum system. Say, a harmonic oscillator, or a qubit or even a string or a m-theory brane. In this model no assumptions are made about the exact nature of the quantum world at that length scale. Instead Cao, Carroll, and Michalakis depend on the geometric properties of Hilbert spaces. (ChunJun Cao, 2016)

By two different mathematical formulations they show how it is plausible that the effect of many many of these Hilbert spaces being entangled can lead to a familiar concept of length, and a space-time metric. They also show how to get a basic ideas of entropy and of curvature and an Einstein Equation out of this. These are all the prerequisites for any remotely plausible theory that could lead to a quantum gravity model. Indeed, being able to get something that resembles the famous result of Bekenstein and Hawking for black hole entropy out of such a model is step 1 for considering it seriously.

Those who are schooled in this topic will recognize how this looks quite similar to the spin foam model from the program of Loop Quantum Gravity. For an example of how Spin foam works check out (Norbert Bodendorfer, 2016) or anyone of a large number of other papers. It is indeed quite similar. There area couple of key differences. There is no idea of spin required for this model. Another key difference here is that the information graphs don’t contain a built in notion of time. So this is more like a spin network without spin. If spin needed to be added it could be as one of many possible properties of the Hilbert spaces at each vertex. One could even call this a quantum information network and look forward to some sort of “information foam” model. (Ooh I should trademark that.)

I will not try to do complete justice to all of the math’s and details of it on this blog. I will say I highly recommend reading this to anyone interested in the subject of quantum gravity. Perhaps an approach like this, which does not make any assumptions about the Planck scale physics is just what we need.

References

Chun Jun Cao, S. M.Caroll, Spyridon Michalakis (2016). Space from Hilbert Space: Recovering Geometry from Bulk Entanglement. arXiv. Retrieved from https://arxiv.org/abs/1606.08444

Norbert Bodendorfer, Y. N. (2016). Imaginary action, spinfoam asymptotics and the ‘transplanckian’ regime of loop quantum gravity. Classical and Quantum Gravity, 30(19). doi:10.1088/0264-9381/30/19/195018