If a particle satisfies the minimum mandated by the uncertainty relation and is subject to no force, the fuzziness of its momentum causes the fuzziness of its position to increase, while the fuzziness of its momentum remains the same. So the amount of information available for predicting the outcome of a momentum measurement remains the same, while the amount of information available for predicting the outcome of a position measurement decreases. This apparent loss of information is made up by an increase in the amount of information that is available for making conditional predictions.

Such predictions are of the form: IF the particle is found hereabouts (by an approximate position measurement) THEN such and such are the probabilities of the possible outcomes of a momentum measurement. Position and momentum have gotten entangled, which means that the outcomes of both types of measurement are correlated, which means that increasing your information about the particle’s position increases your information about the particle’ momentum. Unless the Heisenberg limit is exceeded, no violation of the uncertainty relation occurs.

Now remember Young’s two-slit experiment. 200 years later physicists have learned how to shine light through the slits one photon at a time (or do something very much amounting to that), to do this a large number of times, and to perform measurements that (i) preselect photons with roughly known whereabouts and (ii) yield approximate information about the momentum of the preselected photons. As long as the Heisenberg limit isn’t exceeded, no violation of the uncertainty relation occurs.

For each approximate position one thus obtains an average momentum, and if one maps the average momenta on the approximate positions, one obtains this graph (Sacha Kocsis et al., “Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer“, Science 3 June 2011: Vol. 332 no. 6034 pp. 1170-1173):

Plot of average photon momenta

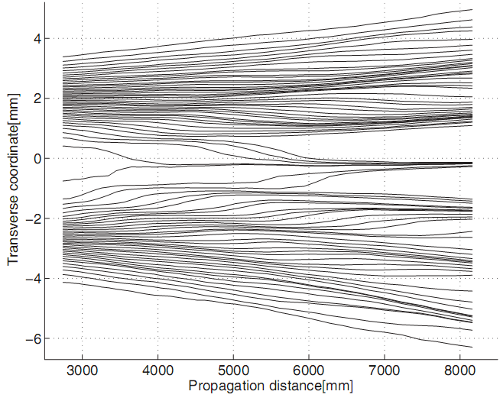
Must I insist that a consolidated plot of (approximately) locally observed average momenta is one thing, and a plot of strictly unobservable Bohmian trajectories is quite another?