
(The lines in these graphs do not represent trajectories; they merely indicate possible identities between the incoming and outgoing particles.) In other words, can we assume that either E is the same as N (in which case W is the same as S) or E is the same as S (in which case W is the same as N)? Does the question "Which incoming particle is identical with which outgoing particle?" have an answer?
Let's calculate. If we denote the respective amplitudes associated with the alternatives (N→E,S→W) and (N→W,S→E) by <EW|NS> and <WE|NS>, then the probability p assigned to this scattering event is
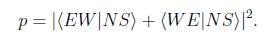
(Eq. 1)
If there are no preferred directions (due to external forces, particle spins, and such), it follows from the mirror symmetry of the alternatives that the absolute values of the amplitudes are equal. The phases, though, may differ. Considered as arrows in the complex plane, this means that the amplitudes are of equal lengths but may point in different directions. Swapping either the incoming or the outgoing particles does two things: it turns <EW|NS> into <WE|NS>, and it rotates <EW|NS> by some angle α. Hence swapping either the incoming or the outgoing particles twice turns <EW|NS> into <EW|NS>, restoring the original situation, and rotates <EW|NS> by twice the angle α. There are therefore two possibilities:
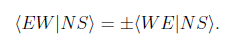
(The positive sign holds for bosons, the negative sign for fermions.) It follows that for indistinguishable bosons p is larger than (in fact, twice as large as) the corresponding probability for distinguishable particles (which are subject to Rule A), while for indistinguishable fermions it is smaller (in fact, zero).
Now suppose that the question "Which incoming particle is identical with which outgoing particle?" has an answer. In this case p is the sum of two probabilities, each corresponding to one of the possible answers. But this is tantamount to Rule A, whereas we are dealing with a situation in which Rule B applies. The question "Which is which?" is therefore meaningless – there is no answer.
Meaningless questions generally arise from false assumptions. The question "Which is which?" arises because we assume that initially there are two things, one moving northward and one moving southward, that in the end there are two things, one moving eastward and one moving westward, and that each thing remains identical with itself. If we assume instead that initially there is one thing moving both northward and southward, and that in the end there is one thing moving both eastward and westward, the meaningless question "Which is which?" can no longer be asked.
Our next order of business is to calculate the amplitude associated with the transition of a pair of bosons from a 2-particle state |i> to a 2-particle state <f|. In both states each particle is completely described by a set of properties – the respective outcomes of four complete measurements. Call the two initial 1-particle states A and B, and call the two final 1-particle states C and D. If we were to write |AB> for |i>, we would introduce, over and above the physically warranted distinction between "the boson with the properties A" and "the boson with the properties B" the physically unwarranted distinction between the "first" or "left" boson (having properties A) and the "second" or "right" boson (having properties B). Ditto if we were to write |BA> for |i>. To expunge the unwarranted distinction we instead write
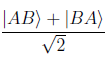
The division by the root of 2 takes care of normalization – at the end of the day, the probabilities of the possible outcomes of a measurement have to add up to 1. (Here we assume that A and B stand for different outcomes of identical complete measurements.) In the case of fermions we need to use the antisymmetric state
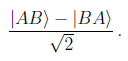
Since no antisymmetric state can be constructed out of identical 1-particle states, the probability of finding two fermions in possession of exactly the same properties is 0. This is Pauli's exclusion principle.
The transition amplitude <f|i> for bosons thus is
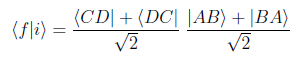
which works out at
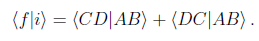
(In arriving at this result, we took into account that the amplitudes <AB|CD> and <BA|DC> are associated with the same alternative.) The corresponding transition probability is

Comparison with (Eq. 1) above demonstrates that we are on the right track.
If A, B, C,... represent different outcomes of the same kind of measurement, properly symmetrized multiple-boson states are obtained by adding all distinct permutations and dividing by the square root of their number. The symmetrized 3-boson states are thus of the form
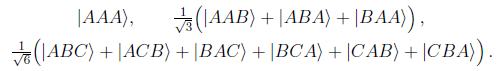
Next question. If n bosons have been found in possession of the same complete set of properties X and one boson has been found in possession of a different complete set of properties Y, what is the probability of finding all n+1 bosons in possession of X? The initial and final states are
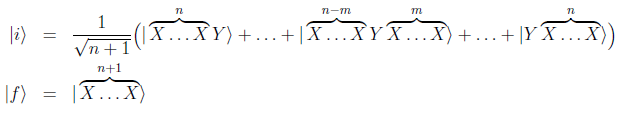
so that the transition amplitude is
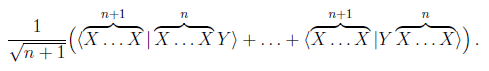
Since the n+1 terms inside the brackets are equal to <X|X>n <X|Y>, this equals
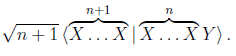
The probability we are looking for,
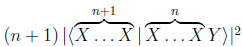
thus turns out to be larger by a factor n+1 than the corresponding probability for distinguishable bosons, whose multi-particle states do not require symmetrization because X and Y are not complete sets of properties and the distinction between |XY> and |YX> is physically warranted. (Distinguishable bosons carry "identity tags", which warrant the distinction between the "first" or "left" boson and the "second" or "right" one.) The bottom line: the more bosons are in possession of a complete set of properties X, the more likely is another boson to acquire this set of properties.
It may be instructive to consider the statistics of a pair of quantum coins or dice. The statistics of fermionic coins or dice is elementary. If two fermionic coins are tossed, there is a single possible outcome (HT, which is indistinguishable from TH), and this has probability 1. (Here we assume that H and T are complete sets of properties!) If two fermionic dice are cast, there are 1+2+3+4+5=15 possible outcomes, each with probability 1/15.
If a pair of bosonic coins are tossed, there are three possible outcomes, HH, TT, and HT (which again is indistinguishable from TH). Let's calculate their probabilities. The probability of tossing an H when there is as yet no H is p(H)=1/2. The probability of tossing an H when there already is one (and only one) H is twice the probability of tossing a T when there already is one (and only one) H since the factor n+1 equals 2 in this case: p(H|H) = 2p(T|H). And since we must have that p(T|H) + p(H|H) = 1, we conclude that p(H|H) = 2/3. The joint probability p(HH) thus equals p(H|H) x p(H) = (2/3) x (1/2) = 1/3. By the same token, p(TT) = 1/3. It follows that the probability of tossing one H and one T also equals 1/3. Observe that the three possibilities are equiprobable, just as in the classical case, where there are four possibilities (HT and TH are distinct in this case) each with probability 1/4.
Let's now assume that there are N possible outcomes A,B,C,... (for quantum dice N=6). The probability of obtaining an A when there is as yet no A is p(A)=1/N. The probability of obtaining an A when there already is one (and only one) A is twice the probability of obtaining a given different outcome when there already is one (and only one) A. Hence p(A|A) = 2/(N+1). The joint probability p(AA) thus equals p(A|A) x p(A) = 2/[(N+1)N].
There are N ways of obtaining the same outcome twice (once with each of the two N-faced "dice"), so the total probability of obtaining the same outcome (no matter which) twice is 2N/[(N+1)N] = 2/(N+1). The total probability of obtaining different outcomes accordingly is 1 – 2/(N+1) = (N–1)/(N+1). And since there are N(N–1)/2 ways of obtaining different outcomes (not counting permutations), each way of obtaining different outcomes has the probability [(N-1)/(N+1)]/[N(N-1)/2] = 2/[(N+1)N] (for bosonic quantum dice, this is 1/21).
Surprise, surprise: all possible outcomes are again equiprobable. Why? Because of the symmetrization/antisymmetrization rule for bosons/fermions, and thus ultimately because we are not dealing with two things each having a complete set of properties but with one and the same thing possessing two complete sets of properties.
Unlike the outcomes of tosses of classical dice, the outcomes of tosses of quantum dice are correlated. For bosonic dice, the probability of obtaining a 6 increases with the number of dice already showing a 6, while for fermionic dice the probability of obtaining a 6 is zero unless no other die is showing a 6. What mechanism or process could possibly explain the correlations that obtain between indistinguishable particles? In their textbook Gravitation, Misner, Thorne, and Wheeler have answered the question succinctly:
No acceptable explanation for the miraculous identity of particles of the same type has ever been put forward. That identity must be regarded, not as a triviality, but as a central mystery of physics.





Comments