If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.In his 1951 textbook, David Bohm reformulated EPR's thought experiment in terms of a dissociating diatomic spinless molecule. The dissociated atoms are in the singlet state and can be separated by an arbitrary distance. In this context, EPR would argue that any spin component of atom 1 can be measured by measuring the corresponding spin component of atom 2 "without in any way disturbing" atom 1. If this were correct, it would follow that the values of all spin components of atom 1 pre-exist.
In Bohm's context, the dubious nature of EPR's claim jumps out right away. In natural units, the possible values of the spin-components of a spin-1/2 particle are +1/2 and −1/2. If the z-component has a positive value, then the component with respect to the inverted z-axis has a negative value. Hence if we continuously rotate the measurement axis from being parallel to being antiparallel to the z-axis, a discontinuous change from +1/2 to −1/2 must occur at some point. Gleason (in 1957) and later Bell (in 1966) formally disproved the possibility of such jumps. Bell however went further, pointing out that Gleason's argument as well as his own "tacitly assumed that measurement of an observable must yield the same value independently of what other measurements may be made simultaneously." In other words, they had both assumed that measurements are noncontextual.
Enter Kochen and Specker (KS). In 1967 they proved a theorem that places constraints on the permissible types of hidden variables. The starting point of their proof was the rather unobjectionable assumption that the pre-existent values of observables A,B,C, which are posited by cryptodeterministic theories, obey the algebraic relations between the corresponding self-adjoint operators A,B,C. Specifically, the values v(A), v(B), v(C) satisfy the following constraints: if A,B,C are compatible, so that A,B,C commute, then
C = A + B implies v(C) = v(A) + v(B),
and
C = A B implies v(C) = v(A) v(B).
For the uninitiated: The probabilities of the possible outcomes of a measurable quantity ("observable") A (as well as such dependent quantities as the mean value or the standard deviation) are calculated with the help of a self-adjoint operator A. If two such operators commute (i.e., if AB=BA), then A and B are said to be compatible, which means that they can be measured together.
KS then showed that, for vector spaces of at least three dimensions, this rather unobjectionable assumption implies that hidden variables must in general be contextual. (While calculating the probabilities of measurement outcomes, one represents the latter by subspaces in a vector space or by the corresponding projection operators.)
An important feature of the KS theorem is that it does not distinguish between systems that are composite and systems that are not. The following demonstration, due to Mermin, uses an array of nine operators in the 4-dimensional vector space associated with a system composed of two spin-1/2 particles:
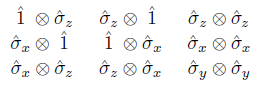
The eigenvalues of these operators are +1 and -1, as are the possible measurement outcomes of the corresponding observables. The three operators in each row and in each column commute, so they can be measured simultaneously. In each row and each column, every operator is the product of the two others, except in the third column, where every operator is minus the product of the two others. Let's assume that the observables corresponding to the nine operators have pre-existent values, and let's designate them by
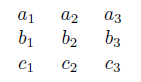
Because the operators in each row and each column of the first array commute, we expect the corresponding values in each row and each column of the second array (all of which are equal to either +1 or −1), to satisfy the same multiplication rules. In other words, we expect that the following equations hold:
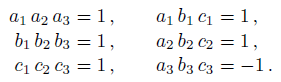
But this impossible: whereas the product of the left-hand sides of these six equations equals +1 (because each value occurs squared), the product of the right-hand sides equals −1.
The long and the short of it is that in general the outcome of a measurement of an observable A, performed on a system S, does not depend only on A and S. It also depends on what other measurements are performed.
Suppose, for example, that eight of the nine values in the second array are as follows:
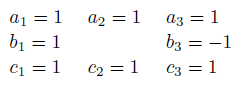
If b2 is measured together with b1=1 and b3=−1, its value is −1. If it is measured together with a2=1 and c2=1, its value is +1. If there was any need for another nail in the coffin of hidden variables, this is it.
The excitement about an experiment recently reported by Radek Lapkiewicz et al. ("Experimental non-classicality of an indivisible quantum system", Nature 474, 490, 2011, DOI: 10.1038/nature10119, arXiv:1106.4481v1) is thus perfectly justified, inasmuch as it demonstrates contextuality not just theoretically but experimentally (implementing a setup designed in 2008 by Alexander Klyachko and colleagues), and this by using a system that is associated with a 3-dimensional vector space, which cannot be carved up into the product space of two component systems.
Zeilinger, at whose Institute the experiment was conducted, concluded that "there is no sense in assuming that what we do not measure about a system has [an independent] reality." (New Scientist, 25 June 2011, p. 13) In other words, to be is to be measured.





Comments