One of the few physics measurements that the LHC experiments are already in the position of producing, with the week-worth of proton-proton collision data they have collected last December, is that of the Bose-Einstein intereference between identical bosons.

I hope I will have a more thorough discussion of this intriguing quantum-mechanical effect soon, when the experiments will have produced results on it: ALICE, the experiment built to study nuclear collisions, has already shown the effect at a CERN public meeting two days before Christmas (see figure at the bottom of the post), so it is fair to assume that papers will soon flourish with a full-fledged measurement. For now, I just wish to give some basic introduction to the phenomenon, since I promised one to a couple of people today!

First of all, what is a Bose-Einstein correlation ? It is an effect connected with the very nature of the wave-function of bosons -particles which are endowed with a integer value of spin. The wave function of a particle "knows" about all its own properties; among them, position and momentum, of course, but also the identity of the particle it represents. And because wave functions are -well- waves, they may interfere with each other. The interference of waves may produce a enhancement, or a suppression, of their individual amplitudes: and amplitudes, in quantum mechanics, are the things with which one computes the probability to find a particle in some place, with some value of its measurable properties.

Bosons have wave-functions that interfere constructively: if you place a boson in a certain point of space, with certain characteristics, then the chance that additional identical bosons will be found in the same location, with the same characteristics of the first one, is enhanced! Bosons are "sociable", so to speak.

Incidentally, the opposite happens to fermions, particles of half-integer spin. The electron is the best example: the probability to find a second electron where there's one is zero, if the two have identical properties. This is the famous Pauli exclusion principle, on which the richness of our world is based: without it, all atoms would have all their electrons on the ground state, and they would have pretty similar chemical properties, preventing the diversity of Mendeleev's table.

But let's stick to bosons -the particles that stick to each other. How can we study whether bosons display this property in a particle collision ?

In general, a proton-proton collision at the LHC produces dozens of hadrons -mostly pions. Pions are particles made by a quark and an antiquark, bound together tightly by the strong force. There are three kinds of pions: positively and negatively charged, and neutral ones. The charged ones live on average about ten nanoseconds before disintegrating; they have therefore enough time to leave the interaction point and cross the silicon sensors which LHC detectors are endowed with at their center, depositing there a ionization charge with which clean tracks may be reconstructed.

What do we do with those tracks ? We measure their curvature in the magnetic field, and determine their energy and momentum. Now, if we find two tracks of the same charge (same direction of curvature in the magnetic field!), lying very close in angle, with the same momentum, then we may imagine that these are actually two pions -identical bosons!- that were mutually influenced during the production process by the quantum interference effect called "Bose-Einstein correlation". An excess of such pairs with respect to a simulation that does not include the quantum interference effect is all we need to demonstrate the phenomenon!

Past experiments have always relied on computing a ratio R of the signal sample divided by a reference sample of track pairs constructed in such a way that they should have no correlation: one thus gets a ratio equal to 1.0 if there is no effect, or a enhancement from 1.0 for track pairs with very close observable momenta if Bose-Einstein correlations are present.

Reference samples can be constructed in a variety of ways: for instance, by taking pairs of tracks of opposite charge: different-charge particles are not identical!; or by taking one track in one event, pairing it up with a track in the next event; or by pairing one track with another whose direction has been swapped by 180 degrees. In all cases, one ends up displaying the ratio R as a function of a specific property of the track pair: a variable which is called "Q-value", basically a measure of how different the two track momenta are. At small Q-value, one observes an enhancement with respect to the reference sample.

Below, for instance, is what was measured by the UA1 experiment at the CERN SppS proton-antiproton collider in the eighties:



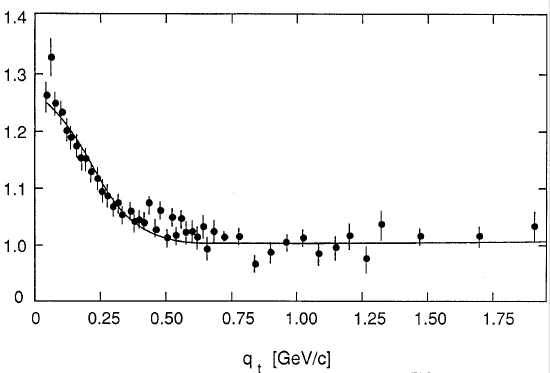
The enhancement at small Q-value is due to the interference of pions. The region of Q where the phenomenon extends tells us about how large is the region of overlap of the wavefunctions, where the interference produces its effect; the height of the enhancement is another parameter, which measures how strong is the correlation.

I hope I will be soon commenting on the first results on this effect measured at the LHC: while the above figure has been obtained by colliding protons with antiprotons at an energy of 630 GeV, nobody has yet measured it with protons against protons at 900 GeV, or a fortiori at the higher energy of 2.36 TeV. I do not expect a large difference, but it will be interesting to compare things.

And now an ounce of competition: I fear that the first experiment to show such results will again be ALICE, given the preliminary plot below, which they already showed last Christmas; and given the impressive speed at which they have shown to be capable to produce scientific publications. But eventually CMS and ATLAS will produce their own results, too!

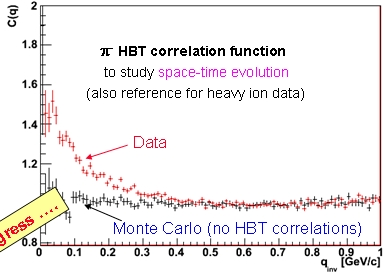On the right you can see the preliminary result (the yellow box on the bottom right says "work in progress...") produced by ALICE. The signal appears, as in the case of the UA1 result, at the lowest values of Q; instead the Monte Carlo simulation, which does not include the quantum-mechanical interference, is flat.

I have however the impression that ALICE will not be beaten on this measurement for another reason besides the speed at which they can approve their results for public consumption: they have shown (see below) that their detector provides an impressive capability of distinguishing particles of different species by using the amount of ionization left by the charged tracks in the silicon layers -a feature shared by CMS and ATLAS but with smaller resolution. ALICE, which is optimized for high-density nuclear interactions, direly needs such a tool.

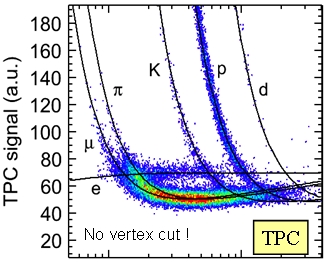On the left, different particles (electrons, e; muons, 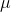; pions, 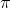; kaons, K; protons, p; and deuterons, d) populate the well-separated bands of points in this scatterplot. The bands appear when one displays for a particle the dE/dx -ionization energy loss per unit material thickness traversed - as a function of track momentum.

The extraction of a signal of Bose-Einstein correlations, which is a phenomenon connected with the particle identity, gets greatly eased by pairing up particles of the same species, rather than having to assume that every track is a pion. That is why a precise dE/dx is important.

In any case, time will tell... Stay tuned for these first interesting results!