Moore's Law, originating in 1965 [1], is an observation of transistor density on a single CPU core increasing exponentially with time. Futurists such as Ray Kurzweil [2] extend this to the claim that CPU-core computation rate (operations per second) will also increase exponentially with time, allowing for a technological explosion of super-intelligent machines in soon-to-come decades.

I, to be clear from the outset, do not agree with Kurzweil et al. for multiple reasons. First of all, he has not justified the assumption that computation speed is the only major barrier to such a technological explosion, an assumption without which his argument fails. But more importantly, as I show in this posting, even if we grant that assumption, computation speed is limited severely by physical considerations.

Any computation device, whether photonic/optical or electronic, must have internal states corresponding to '0' and '1' as well as an interaction between these internal states which occurs via some physical process. Furthermore, information must be contained in the electromagnetic field. This is because electromagnetism is the only interaction that can be used for processing. Gravity only works with large (and therefore sluggish) bodies, and the strong and weak nuclear forces are confined to subatomic processes that are too noisy to control due to quantum fluctuations.

Optical/photonic information processing uses electromagnetic fields of radiation, and electronics keep the information in voltages, which represent electric potential associated with electric fields in and around transistors. So I hope it is now clear that, in order to compute, you must work with electromagnetic fields. In practice, in the vast majority of cases, the electric field is more important than the magnetic one, spintronics [3] excepted. So I will frame this discussion in terms of electric fields, but a similar argument can be made in the magnetic case as well.

In order to be able to have distinguishable '0' and '1' states that can interact via the electric field, one needs to have an electric field strength larger than the background noise, as anyone who has used an oscilloscope can attest. Noise has many sources, including manmade noise, solar noise, thermal noise, and quantum noise.

The amount of quantum noise is strongly dependent on the frequency of operation. Modern processors in the Gigahertz range are commonplace, and at this low a frequency, quantum noise in the electric field is negligible. As I will show, above a certain frequency (and thus above the corresponding computation rate by the Shannon sampling theorem[4]), computation is not possible without destroying the computer almost instantly. (Readers not well-versed in physics and math may skip to the 'Discussion' section)

Derivation

Very roughly, the electric field required to overcome quantum noise (and thus necessary to compute) satisfies the relation: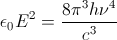



where 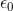  is the permittivity of free space,  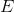is the electric field strength, 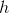is Planck's constant, 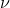is frequency, and  is the speed of light in free space.

This is equivalent to electromagnetic radiation at a central frequency of order 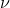   and intensity     .
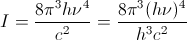Using a value of 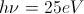, which is sufficient to ionize atoms of all elements and thus will be strongly absorbed by all materials, this comes out to an intensity equivalent required to compute of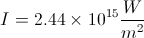



For scale, frying an ant with a magnifying glass in under 10 seconds requires only about 2 MW/m^2, which is lower by a factor of about 1 billion! The Shannon sampling theorem [4] says that, since information transfer, and thus computation, can only proceed at a rate of twice the maximum frequency involved,
 this 10 nanosecond computer destruction can only be avoided by keeping computation rates below .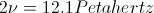

Discussion

The computation speed would be capped at 12,100,000 GHz. Any attempt to surpass this would require electric fields so high that your computer would be fried almost instantly. Kurzweil is wrong, and CPU speed cannot continue increasing exponentially, even in principle.

P.S. if you're thinking about this scale of super-bright high-energy radiation, don't try it at home. It will fry you in a split second, too!


References

[1] http://en.wikipedia.org/wiki/Moore%27s_Law
[2] http://en.wikipedia.org/wiki/Ray_kurzweil
[3] http://en.wikipedia.org/wiki/Spintronics
[4] http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem