First of all, what experiment are we talking about? It is called "MUonE", and it aims at measuring with the utmost precision the rate at which muons scatter elastically off electrons, as a function of the transferred energy of the scattering reaction.
The reaction proceeds, in the overwhelming majority of cases, by the electromagnetic interaction, mediated by the exchange of a single photon (a space-like one, if that means anything to you). But in the quantum world, everything overlaps with everything else: so there is a small but non-negligible contribution from processes where the photon temporarily "splits" into quarks. By measuring precisely the muon-electron scattering rate, the MUonE proponents hope to pinpoint the size of that small contribution (called "hadronic contribution" in the following), which has a large relevance in a totally different measurement, that of the anomalous magnetic moment of the muon.
The elastic scattering process per se is a very simple thing: you direct a beam of muons against a fixed target, where the oblivious electrons mind their own business, lazily spinning around their nuclei. Occasionally, a muon kicks an electron off by throwing a photon at it: both electron and muon then emerge from the target with some angular divergence from the initial muon direction. You measure the trajectories of incoming muon and outgoing muon and electron, and count how many you see as a function of those angles. And you are done. Easy to the point of being boring? Not really.
As Richard Feynman used to say, anything is interesting if you study deeply enough. The precision required by MUonE to extract the hadronic contribution to the scattering is of a part in a hundred thousand. This can only be achieved with a detector which is both very precise and robust to backgrounds and systematic uncertainties of all kinds.
Enter MUonE
The experiment is planned to be built at CERN, where a beam of 150 GeV muons with suitable intensity is available. Since you need to track particles without affecting their direction (so that you can precisely estimate angles), the setup foresees the use of precise silicon microstrip detectors, which collect in densely arranged strip electrodes the ionization charge left by the electrically charged particles as they traverse 320-micron-thick silicon sensors. The strips are separated by 90 microns; by alternating layers where strips are laid in one direction and in the orthogonal one, one gets to 3D-track the ionizing particles with position uncertainties in the 10-micron range.
The layout proposed for the experiment foresees 40 identical measuring stations, placed in series one donwstream the other. The idea is that each station can both track muons before they interact in the following ones, and track muons and electron emerging from the target after an interaction has taken place. The setup of a 1-meter-long (okay, 40 inches, you spoiled non-metric brontosauruses) station is shown below. Muons enter from the right, and they get tracked in three silicon modules.

Many options
My original interest in the experiment is due to my (now terminated) involvement in the "Commissione 1" of INFN, where new proposals for scientific endeavours in accelerator-based physics are discussed. When I got to know about the experiment I studied the matter in some detail, and I came to the conclusion that a different arrangement of the target and detection elements could provide benefits to the measurement. However, there is nothing easy about figuring out on the back of an envelope what resolution one may achieve in the tracking of subnuclear particles by the use of this or that experimental choice, so I figured I needed to simulate the physics of the interaction and the reconstruction of the events kinematics to prove my points.
I therefore started to code a simulation program which could produce simulated elastic scatterings, as well as simulated charge deposits in the active elements of the detector, when the latter was allowed to change configuration with optional parameters chosen by the user (me). The program had to take into account the physics of the scattering, the physics of the modifications of trajectory and energy that particles undergo in traversing matter, the physics of charge deposition and collection in the sensitive elements. And it had to then use the collectable information in a reconstruction of the meaningful measurable quantities - the particle angles, from which one obtains an estimate of the energy transfer of the scattering reaction. Only then would I be able to compare the merits of different detector geometries.
The above looks like a tall order. And it is. If you want to be accurate, there are a large number of small details that require a farecul modeling (pun intended). The program grew to something which is over 7700 lines long now. I would bet a testicle that there still are bugs in it, even after weeks spent polishing it off. But eventually, I am confident that any remaining issue is not affecting the results appreciably. The simulation code provides the answers I wanted, plus more. In fact, while performing the exercise of modeling the detector and the scattering I realized that there were a number of smart little tricks which could improve the capabilities of the experiment.
Thou shalt stagger thy strips
Below I show one graph taken from the article, which proves how the relative resolution in the energy transfer (we call it "q-squared"), as well as in the individual angles of incoming and outgoing particles can improve by over 40 percent if a tiny modification is operated on the assembly of the double-sided silicon sensors that MUonE plans to use.
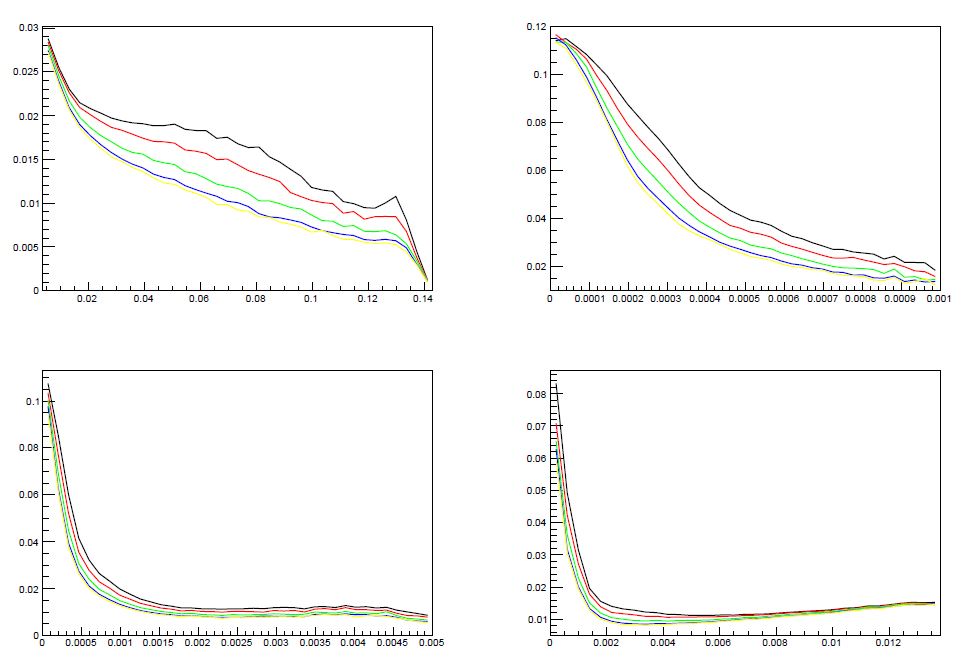
Above, the top left graph shows the relative resolution in q-squared as a function of q-squared; the top right graph shows the relative resolution in incoming muon angle off the beam, as a function of the same angle; the lower left graph shows the same for the outgoing muon; and the lower right graph shows the same for the electron. In all graphs, the black curve is the nominal resolution, the yellow one (lowest curve in all four graphs) shows the resolution one may obtain by "staggering" by 45 microns the strips on one of the two sides of the sensors with respect to the other side.
I have shown this result here because it is one of the most striking, but also one of the easiest to understand intuitively. Each of the silicon modules measures particles twice as there are two back-to-back measuring devices separated by 1.8mm from one another. Since particles incide with almost exactly orthogonal trajectories, the two measurements determine the same cooridinate (vertical in the graph below). The discreteness of the measurement device (strips spaced by 90 microns) causes the two measurements to act as one. If the strips are staggered by half strip pitch, instead, the resolution improves by a factor 2!
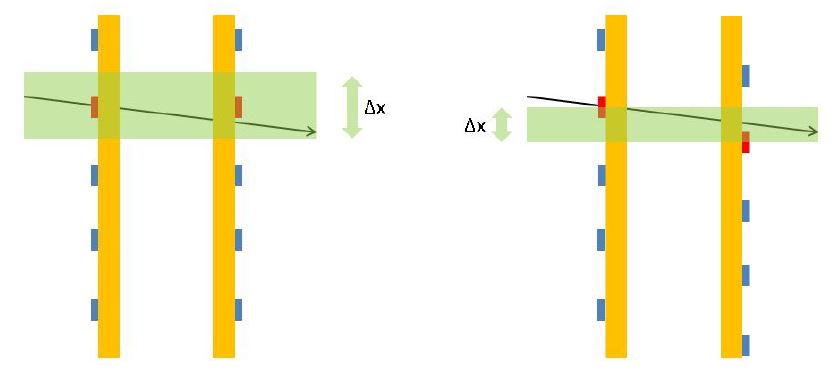
[For the unconvinced folks out there: the probability density function of the measurement is a box distribution, not a Gaussian, so your guess that the improvement is by a factor sqrt(2) is wrong!]
At the end of my 54-page article I was able to put together a list of recommendations which I hope may help the design of a more performant detector. I paste them below for the really nosy among you. If you are interested in the matter, I suggest you to also download a copy of the article here, one day before it appears on the arXiv!
Recommendations
- The advantages of an independence of the stations making up the detector (ease of construction and assembly, reduction of trigger logic) should be considered with care and compared to the advantages brought by the alternative designs proposed in this work, to be reassessed with a full simulation of the detector and interactions.
- The option of dividing up the target material into as many thin layers as it is practical to assemble in rigid structures should be investigated in detail, taking into account material choices, production costs, and machining issues. The single choice of dividing the 1.5 cm of beryllium envisioned for each station into 300 50 μm thick layers, stacked into 31-cm-long structures where each layer is spaced by 3mm from its neighbors, wins a considerable amount of constraining power on the parameter of interest.
- If shorter stacks of thin target layers are built, which thus do not occupy the full longitudinal space between two consecutive modules in a section, their placement with respect to the tracking modules should be studied with care, as considerable variations in the q-squared resolution may result from the variation of that parameter. From our studies it appears advantageous to position the target stacks closer to the module on their left, as this increases the precision of the measurement of outgoing particles at the price of a less crucial decrease of the precision with which the incoming muon is traced.
- The construction of double-sided silicon strip detection elements should be customized such that one side has strips staggered by half the pitch width (i.e. 45 μm for the CMS Phase-2 sensors) with respect to the position of the strips on the other side. While the advantage of such setup depends on the details of the charge collection in the sensors, which has been simulated with a quite crude model, we believe that the peculiar kinematics of MUonE, with almost all tracks traveling with almost null divergence from the beam axis and thus will typically create single-strip hits, makes this conclusion robust.
- The option of rotating by a 45-degree stereo angle the middle module of each station should be studied with a full simulation which could appraise the relative merits of such a setup with respect to other effects. In the absence of backgrounds and in the idealized setup we have considered here, a slight worsening of the considered figures of merit is apparent from the rotated setup. In addition, a small loss in acceptance results from the misalignment of the sensitive area of the second module with respect to the other two in each station.
- If practical, the separation of sensors in double-sided modules by a larger amount than the 0.18cm default of the CMS phase 2 detection elements appears to improve the resolution for the reconstruction of elastic muon-electron scattering events, in modules mounted with no staggering of the strips; however, if a 45 μm staggering is used in mounting the two sensors back-to-back in a double-sided module, the spacing should be kept at its minimum value.
- Although in principle advantageous, the production of thin layers machined in a square lattice by etching away material in a grid of narrow holes does not appear to provide a sufficient additional constraining power to be worth pursuing, as the resolution on the transverse position of the scattering vertex achievable with a combined fit to the three tracks is already quite good.
- We suggest that the positioning, the tilt, and the bow of each of the detection elements can be determined with very high accuracy by studying the distribution of the profile likelihood of the scattering fits to a large number of interactions as a function of the considered biased parameter. In order to evidence those shifts and constrain the parameters in an optimal way, the fits should handle the scattering as a whole as is done in this study, rather than consider independently the trajectory of each track.
- In case a distributed target is chosen for the detector, the option of sealing the volume external to the tracking modules in bags filled with low-pressure helium should be considered. While we did not compare the resolution provided by such an arrangement to that obtained by ignoring the effect of scatterings in air, a small gain is clearly predictable by reducing the scattering with non-constrainable vertex z.
- We suggest that a global likelihood fit to the track hit information, which included the hit position determination in the likelihood calculation, would improve the sensitivity of the determination of the event q-squared over other choices. The benefits of a simultaneous fit to all available information comes from avoiding first-order Taylor approximations to the covariance of the individual determinations, as well as, in the case of hit finding, from the interplay of the center-of-gravity determination and the track incident angle on the silicon sensors. We are however aware that the presently envisioned readout of the CMS phase-2 silicon modules does not include analogic charge readout capabilities, so this option may not be implemented in practice.





Comments