Different techniques for muon tomography
While muon tomography is a very well established technique in general, which is successfully used to obtain radiographies of volcanos, archaeological structures, foundries, or containers crossing borders, the methods used for imaging the unknown volume are essentially confined to two bits of physics: the fact that muons scatter more visibly from a straight trajectory when they traverse denser material, and the fact that they get absorbed more if the material they traverse is denser.
Instead, so far I believe nobody has ever considered seriously the possibility of exploiting the phenomenon called k capture.
K capture in a nutshell
Negatively charged muons are like heavier replicas of electrons, so when they stop inside matter they may get captured by an atomic nucleus (which is positively charged). As they spiral into the nucleus muons emit a series of X rays that are very specific of the nucleus that is dragging them in; and as they settle in the lowest-energy orbit - so called "k-shell" -, they spend time in the company of protons, and end up interacting with one of them. The resulting reaction transforms the muon in a neutrino and the proton in a neutron; the two final state objects fly away with a few tens of MeV each.
To summarize, negative muons stopping in material do *not* decay with the lifetime that muons have when free particles (2.197 microseconds): rather, they die more quickly, with a lifetime that is strongly dependent on the atomic species of the nucleus they fell into. Also, what is emitted from the decay is not an electron and two neutrinos, as in their regular decay, but a neutron and a few X rays.
Can we use it?
Can the above complex physics be used to concoct a third tomography method using muons? Well, the answer depends on two things. One, the availability of an intense enough source of soft negative muons; and two, the capability to detect the results of K capture and track them back to the point of decay. Let us consider the two points in more detail.
Muon tomography until today has been relying on cosmic rays. Cosmic rays impinge on the earth's atmosphere from the cosmos. They are typically protons or light nuclei, that hit hard an oxygen or nitrogen atom and produce a cascade of secondary particles - mostly pions and kaons, plus photons. Pions and kaons then decay yielding muons, and muons manage to reach the ground thanks to their penetration power (they interact only weakly with the atmosphere and with matter).
The flux on the ground is of about one muon per square centimeter per minute, so it is rather weak; nonetheless, this is sufficient for "long exposure" tracing of the muon flux through unknown volumes. E.g., if you are looking toward a volcano, your area of interest may be of the order of a square kilometer, and through it you may expect to get over 10 million muons per second; however, only a small part of them will be detectable, as most of the incident flux will be absorbed.
Not only cosmics
When discussing the imaging of smaller surfaces or volumes, the limitation due to the flux becomes important. However, recently some companies are developing portable muon sources - basically compact accelerators that produce muons by the Bethe-Heitler mechanism. This opens the way to exploit phenomena that are much less frequent, such as, indeed, K-capture. For K-capture can only happen if muons stop in matter, so this requires muons to have a very specific energy - basically few hundred MeV, which allows them to penetrate into the scanned volume and then stop there.
So, the first issue can be solved with these technological advancements. But how about the second? Is it really possible to track back a neutron emerging from a surface to the point of origin? Let us consider the setup pictured below.
A concrete use case
Imagine you want to study the detailed composition, in terms of the composing atoms, of an antique mosaic. You might, for instance, be interested in knowing what materials were used, or what lies below. You have no access below the surface, but you can place a muon tracking detector above it. Also, you place a neutron detector very close to the surface, as shown in the sketch below (the downward vertical direction is toward the right in the drawing). This may be a cheap detector, which cannot detect the direction of the neutron, only its arrival time. Also, we are being cheap here as we do not imagine we can afford to detect the soft X rays.
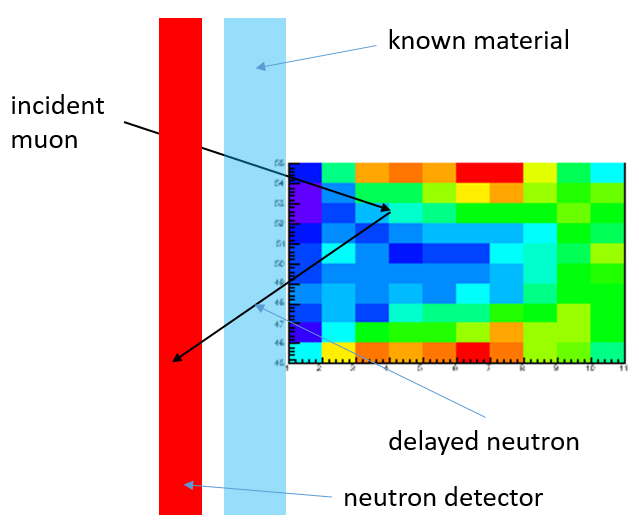
[The colour map in the voxels of the volume of interest (which in the drawing is assumed to be at a depth of two centimeters below a surface layer of known composition) shows the number of detected decays in each voxel according to the simulation, which assumes a flux impinging with angles from -0.7 to 0.7 radians from the left. It is only one of the possible arrangements, and it bear no big effect on the conclusions we will draw from the study of this setup.]
Negative muons may be shot into the surface through the detection system, and if they have the right energy they will stop in there. Then, the magic happens: they spiral into the nucleus, emit X rays, and then turn a proton into a neutron; the neutron, half of the time, emerges back up (if it can travel far enough, which also depends on the composition of the material) and gives a signal in the neutron detector.
What you have in your hands are the incident muon direction and the time that it took the muon to decay in the material. Can this be used to infer the material composition inside some unknown depth of the mosaic? The answer is yes. The fact that muons impinge on the same spot from different directions implies that you get information on the lifetime from many angles, and with a smart enough software you may disentangle the different contributions and obtain a 3D map!
A proof of principle
To prove the above, I wrote a quick and dirty simulation of the process. I assume that muons can be impinged on a volume from different directions, and their incident direction is measured with absolute precision; this is a good enough working hypothesis, as modern muon detectors can track these particles with milliradians uncertainty. Muons then travel into the material, and they have a certain probability of stopping at some depth. Then a simulation of the decay produces a neutron that is shot out in any direction, and - if not absorbed in the material (this depends on the length of its path) - gets detected by the neutron detection layer.
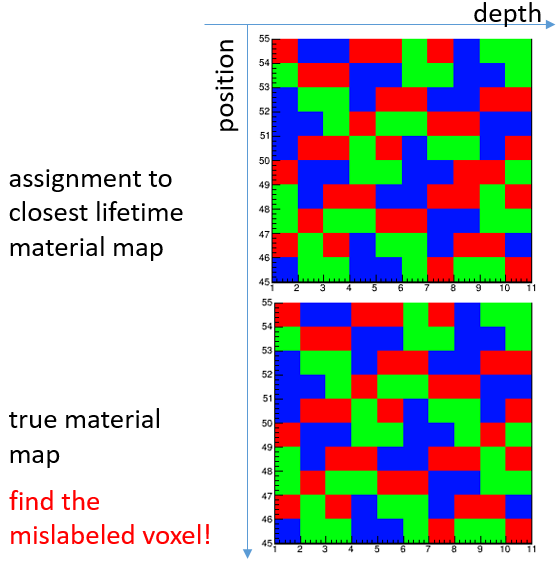
The data generated by the above simulation (muon directions, neutron stopping times) are fed into a likelihood function which depends on a large number of parameters - one lifetime per considered "voxel" of the unknown material. I tried a simple setup with 100 voxels, distributed in 10 layers of 10 columns. Using 200,000 incident muons, and a total of about 67,000 detected decays (some of the neutrons get absorbed, many are emitted further into the material and can't be detected). The likelihood maximization is very complicated, given the 100 free parameters, so rather than feeding the problem into a generic minimization routine, I wrote a custom gradient descent routine. It is slow, but it works.
Below you can see that the reconstructed and true maps of the material - here assumed to be composed of three atomic species, calcium silicon and carbon - is almost perfectly (99%) reproduced by the reconstruction, with a dataset that could be acquired within minutes if a decent muon source is used. This proves that in principle one does not need directionality of the detected neutron, nor information on energy and direction of the emitted X rays. Of course, if one has more money to spend, that can be added to the experimental layout, improving tremendously the performance.
What is next? I think the custom simulation I wrote is only sufficient to give a "proof of principle", but it should be improved in many ways (considering multiple scattering, which for now has been neglected; modeling more precisely neutron attenuation in the material, which can be a further source of information; including the resolution terms of muon direction; etcetera). A good project for a laurea or PhD student!
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments