The rationale is that if it is a viable, patentable idea worth something, once it is published here it becomes of public knowledge and hence non-patentable anymore... Which in turn means nobody owns it, and it can be exploited without problem, like the Salk vaccine.
Of course if you read into the above text, you already know that the idea is probably worthless, but just for fun, let me explore it with you - if nothing else, it still involves the need of discussing interesting physics...
You may know, or better still for you, not know, that in order to treat patients with some kinds of non-operable tumours, we can resort to radiation-assisted methods. There are two things needed here: one, an accurate imaging of the area of the body which needs to be destroyed or ablated; and two, a method to bloody do it; that is, a non-bloody method, for sure. With beams of photons or, better still, protons or light nuclei (e.g., carbon ions), it is possible to irradiate tumours and thus kill them. Some features of protons or carbon ions traveling in matter at specific energies make them very useful, in particular, as they tend to deposit most of their kinetic energy when they come to a stop (causing the so-called "Bragg peak" in energy release). But before we can do that trick, we need to exactly know where the malignant cells are.
Imaging a tumour in the human body is not too difficult, but it has some drawbacks. One technique is to inject the patient with some substance that gets preferentially absorbed by the malignant cells, and if the substance is a fast radiation emitter you may then detect the radiation and reconstruct a 3D image of the area. PET scans work that way, for example. A second method is to target the area with a beam of protons, and infer the composition of the involved tissue by reconstructing the proton trajectories (protons are scattered at larger angles by heavier nuclei). The latter is a form of tomography which is also employed in other use cases using cosmic rays as the probes.
Both techniques above have the shortcoming that there is collateral damage: the patient receives a dose of radiation to healthy tissue during the imaging process. I am not a physician so I will abstain from discussing how relevant this problem really is, but it is important to mention it when considering alternatives.
Now, let us consider muons. The muon is a heavier replica of the electron. It is an elementary particle which decays in 2.2 microseconds, on average, to an electron and two neutrinos. It is electrically charged, as its lighter brother, and undergoes weak or electromagnetic interactions. Because of its large mass (200 times the electron), it typically deposits only a very small amount of energy when it traverses matter.
But more of interest here, the negative muon (the one charged like the electron) does a fun trick when it gets stopped in matter: it withstands the attraction of atomic nuclei, and "falls down" to a tight orbit around the nucleus, when it actually spends a significant part of its time nudging with protons and neutrons. For remember, the muon is 200 times heavier than the electron, so its orbit is tighter. This phenomenon is called "K capture". During the fall into the nucleus, the muon releases a few X rays which are experimentally very useful to flag the occurrence of the phenomenon.
Once the muon is orbiting the nucleus in the inner shell, it can interact with protons by an inverse beta reaction, producing a neutron and a muon neutrino. This phenomenon releases a fast neutron, which can be detected and further "tag" the process. Most interesting is the fact that the probability for this inverse beta decay, and thus its speed of occurrence, is highly dependent on the kind of nucleus that the muon is orbiting: indeed it is possible, at least in theory, to identify the kind of nuclei that absorb negative muons by just collecting a handful of timing measurements. For, while a free muon has a lifetime of 2.2 microseconds, the lifetime of a muon K-captured in different nuclei can be one order of magnitude smaller, and varies very significantly with the atomic number.
Why is all of the above relevant for 3D imaging? Well, imagine you select a substance with which to inject your patient, which contains atoms easily identifiable by the muon lifetime through the inverse beta decay process. The substance needs not be radioactive, as in the normal PET and similar setups! This is the main bonus of the whole thing.
Then you strike the patient with a beam of very soft negative muons - ones which are likely to be stopped in the area of interest. These muons will cause very little damage to the tissue, and you do not need many of them: you have a very effective tracer of the nuclei that do the K capture by reconstructing the emitted neutron and the gamma rays. Those guys will also release some energy in the surrounding tissue before being detected by your equipment surrounding the patient, but this is a minor dose if compared with doses delivered by other means. Or so I think.
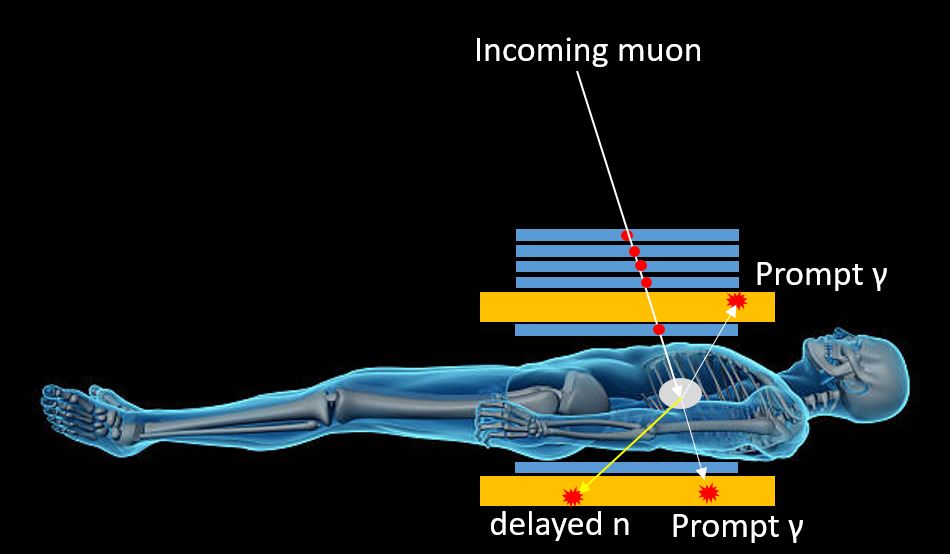
Above, blue rectangles show tracking detectors in section; they detect the incoming muon trajectory and allow, together with the recorded position of the decay signals, the precise location of the K-capture and decay point. Orange rectangles show scintillation detectors useful for the recording of the timing, energy and position of the prompt photons emitted by the muon as it spirals toward the nucleus and the neutron emitted by the inverse beta decay process.
In summary: get a soft muon beam; inject the patient with a non-radioactive, target substance; surround the patient with neutron and gamma detectors; shoot the beam at the interested area, with just enough intensity to obtain a few tens of thousands of K captures per square centimeter; detect the timing distribution of emitted neutrons, with respect to the triggering signals of the gamma rays; and reconstruct the 3D image. Simple, ain't it?
Yes, it seems rather straightforward. But muon beams can't be produced in your garage, in fact. Muons are produced as secondary products of interactions of a beam of protons with a fixed target. You need a synchrotron or some linac for the protons, then a decay tunnel where pions and kaons are allowed to decay into muons, and a set of magnets to collimate the muons into a workable beam of the right energy. And you need to control emittances, intensities, repeat rate, shielding from backgrounds, and all sorts of other things.
At CERN this can be done, and at Fermilab also; but there are not many facilities that can set something like this up in the matter of a weekend. Nevertheless, if this technology were indeed promising (I actually doubt it can be done in practice - maybe because I heavily underestimated the dose that the patient would receive in order to extract a meaningful 3D image, or maybe because there are no suitable substances that can be injected and provide the necessary, distinguishable target), one day it will probably be done.
And now that this piece is published, it cannot be patented, so this text is my gift to humankind, like Jonas Salk's anti-polio vaccine ;-)
---
Tommaso Dorigo (see his personal web page here) is an experimental particle physicist who works for the INFN and the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the MODE Collaboration, a group of physicists and computer scientists from eight institutions in Europe and the US who aim to enable end-to-end optimization of detector design with differentiable programming. Dorigo is an editor of the journals Reviews in Physics and Physics Open. In 2016 Dorigo published the book "Anomaly! Collider Physics and the Quest for New Phenomena at Fermilab", an insider view of the sociology of big particle physics experiments. You can get a copy of the book on Amazon, or contact him to get a free pdf copy if you have limited financial means.






Comments