I am reading a fun paper today, while traveling back home. I spent the past three days at CERN to follow a workshop on machine learning, where I also presented the Anomaly Detection algorithm I have been working on in the past few weeks (and about which I blogged here and here). This evening, I needed a work assignment to make my travel time productive, so why not reading some cool new research and blog about it? What is more, my flight is being delayed and I am stuck in the gold Air France lounge in Geneva, poor me - so the Tawny port they serve there is a very good lubricant for my sticky fingers.

The characters of the play - 1: Dark matter

Dark matter (DM) is an inferred substance permeating our Universe, which is abundant enough to modify the rotational velocity of stars around galaxies and to create other macroscopic effects. Through galaxy rotation speed measurements as well as detection of gravitational lensing of distant galaxies, whose light reaches us after passing through dense galaxy clusters in the line of sight, we have collected a pretty good understanding of the total amount of this substance in our Universe. And yet, we do not know what it is.

There are a large number of possible explanations for the above astrophysical observations, but the ones that appear most convincing predict that there exist neutral, low-interaction, and perfectly stable subnuclear particles which were created in the big bang, and are still traveling around today. Explicit theories provide more detail on what their mass and properties could be, but it is fair to say that any honest-to-god experimental search should try to make no explicit assumptions, as theorists are, arguably, wandering in the dark. What we can admit is that one targets as wide a range of defining parameters as possible. One may also make loose assumptions on their population and speed field of DMaround our planet.

For particle dark matter searches, the two crucial parameters that describe the phenomenology are the mass and the interaction probability of DM particles with ordinary matter (i.e., protons). Explicit theories like Supersymmetry, wherein DM is constituted by the particle called "neutralino", are currently being tested by a number of experiments that try to detect these rare DM-proton interactions by traditional particle physics means, in underground detectors that are thus shielded from the otherwise disturbing background caused by cosmic radiation.

And what is Brownian motion?

Ah, this is a very, very nice little phenomenon that was discovered almost 200 years ago. Its beauty lays in the fact that it is a bridge between microscopic and macroscopic phenomena. We know that gases and liquids are ensembles of molecules in constant motion. The kinetic theory of gases explains lots of thermodynamic phenomena by just modeling molecules are balls bouncing around and off one another; in liquids, things are similar. You can explain the volume of a liquid mass, its pressure on container walls, and other physical properties with very simple models that see these molecules bouncing around, tightly packed but still free to exchange impulse in collisions.

What reverend Brown observed in 1827, with a microscope, was that a suspension of pollen in water showed a constant random motion: the pollen was constantly hit by water molecules, but the total transferred impulse was uneven, and sometimes caused the pollen to move one way or the other. It was Albert Einstein who explained this observation in the context of the atomic theory, and later another giant, Jean Perrin, studied the phenomenon in detail (he got a Nobel prize for his studies of atomic theory of matter).

Of zero relevance to the rest of this article, but still nice to point out: one nice thing about Brownian motion is that the displacement of the observed object follows a very simple quadratic law. What this means, is that if you observe the position of an object subject to Brownian motion at time t=0, and set the "original" coordinates then (say, [X0, Y0] on a microscope field of view), and then observe its position at times t1, 4*t1, 9*t1, 16*t1, etcetera, the expected displacement from [X0,Y0] at those times is Z, 2Z, 3Z, 4Z... What that means is that the displacement follows a square-root law of the time. Ain't that amazing?

The concept of random walk has been studied in a number of systems, and there's a whole branch of Statistics that deals with the concept. So I thought it was cool to mention it in passing by...


DM and Brownian motion

So what is this new idea? If you look at the motion of a tiny particle you might be able to detect, on top of other random effects, the occasional bumps of dark matter particles on it. You might not be able to prove that the offender was a DM particle, but if you collect enough statistics, and show that the bumps come from the direction of motion of the Earth relative to the DM "wind", you just might convince your peers.

In truth, the above sketch is not what the authors of the above mentioned paper propose. They prefer to use a technique based on interferometry, inspired by the recent successes of the LIGO/VIRGO collaboration in detecting sub-atomic-scale displacements due to the space deformation effect of gravitational waves. In their setup they consider 1 mg (milligram) detection elements (the LIGO mirrors have masses of 40kg). The smallness of the mass of the passive target allows for more sensitivity to small momentum transfers from DM-matter interactions. Also, they get sensitive to the momentum of the DM objects. That is very cool, I think.

You will have to read their preprint to know more details. Here, it is only useful to show the money plot of their study, which describes the sensitivity of the proposed setup to light dark matter (in the sub-GeV range which is hard to study with other detector concepts).





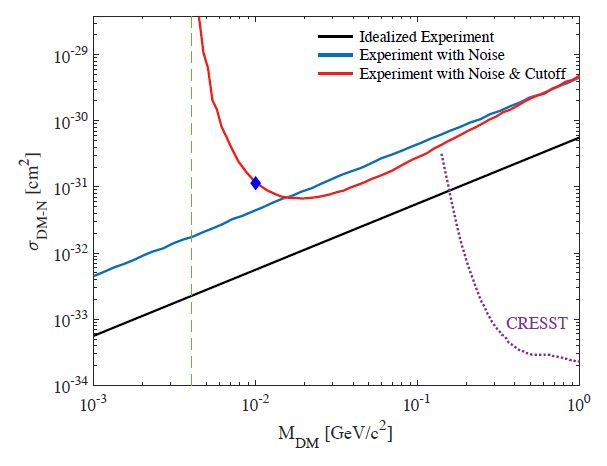
The x axis has the dark matter particle mass in GeV, in a logarithmic scale: you can see that the region of interest is in the MeV region, one where other experiments have little to say because of the small momentum transfer that a DM particle may impart on a single nucleus. The CRESST collaboration sensitivity curve, shown on the right, stresses this point quite clearly. On the y axis is plotted the DM-matter interaction rate, in cross section units (square centimeters). It would take a couple of blog posts to explain why you can describe an interaction rate in terms of an effective area, but intuitively you can probably grasp the idea anyway.

What is interesting in the graph is the red curve, which delimits the region where the proposed experiment could say whether DM exists or not. That is to say, if DM has a mass in the 10 MeV range, say (10^-2 GeV in the x axis), and it has a cross section of 10^-30 cm^2, the experiment should be able to detect it.

I do not know whether in the end this technique is really feasible, but the paper was fun to read. I would be happy if it led to a real experiment, too!

---

Tommaso Dorigo is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journal Reviews in Physics. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon.