I am currently at a turning point in my yearly course on particle physics for statisticians (yes, there is such a course in the Master of Statistical Sciences at the University of Padova - I invented it, with the encouragement of prof. Bruno Scarpa, a few years ago with the aim of bringing statisticians closer to the problems of statistical inference in fundamental science). After describing the rise of quantum physics and the first experiments that proved that our world is made of elementary particles, this week I have been explaining what were the crucial experiments that determined the inner structure of nucleons - the constituents of atomic nuclei, i.e. protons and neutrons.
The whole story is fascinating on oh so many levels. It is an epic tale of experiments, intuitions, diatribas, evidences and counter-evidences what led in 1964 Gell-Mann and Zweig to categorize all known particles until then discovered in particle collisions (and the many more that followed) into so-called "supermultiplets" of the SU(3) group. But that is only part of the whole thing. While Gell-Mann's "eightfold way" managed to frame each hadron in a beautiful picture, much as Mendeleev's table had done for atoms a century earlier, his model did not tell anything about the dynamics of the systems, only explained their static properties.
When we say, by reading it off one of the SU(3) diagrams of the static quark model, that a proton is made of two up quarks and a down quark, we are 1% right and 99% wrong. We are right only inasmuch as our sentence explains that the proton has charge +1 (as the sum of the three quarks charges, +2/3 +2/3 -1/3), zero strangeness, one unit of baryonic number, and a few other static properties. But the proton is not a butterfly that can be nailed with a pin in a display case: it is a garbage bag, in constant motion, and whose internal content changes by the attosecond.
The experiments I told my students about this week were ones that followed the path traced by Ernest Rutherford and his collaborators Geiger and Marsden at the beginning of the past century: when you want to image an object too small to be watched with a microscope, throw something hard at it. Scattering experiments have since probed the structure of matter deeper and deeper, and in particular the deep inelastic scattering experiments of the 1950ies and 60ies were instrumental in providing us with a much clearer picture of a proton than what we can desume from the SU(3) graphs.
What is deep inelastic scattering? In trying to understand what inside a proton, we need to hit it hard with something small. Now, let us imagine the proton as a bag of garbage: it does contain three "valence" quarks, the u-u-d that give it its static properties, but it also contains a lot of other messy stuff we need to sort out. Let the quarks be small and hard things inside the bag, like, say, three beer cans. The bag will however contain also a lot of tissue paper, plastic bottles, glass bottles, maybe some exhausted batteries (but don't do that, please recycle). If we want to know what is inside a garbage bag without opening it, and throw something at it, this something had better be small and hard: that way, by studying the direction that our projectile takes after it penetrates the bag and exits on the other side, we may infer the content of the bag. If we instead used another garbage bag as a projectile, we would create a very messy collision, stuff of all kinds woud fly around in all directions, and we would have a very hard time figuring out what has happened.
In essence, the above is the reason why the experiments aiming to probe the structure of the proton used high-energy electrons as the projectiles. When an electron hits a proton, essentially three things can happen. If it has low energy, it most of the times bounces off gently, leaving the proton unharmed: this is called elastic scattering. Raise the energy of your electron accelerator and you get in a regime where the electron can sometimes "excite" the proton. The proton becomes for an instant a different particle - a delta, eg.- but then regains its nature; this is called semi-inelastic scattering. If the energy of the electron is still higher, however, it can break apart the proton and create a mess of pieces that fly out in all directions: in this third regime, called "deep inelastic scattering", we have lost track of the proton in the final state of the reaction, and must describe the resulting particles collectively as a "hadronic system".
The reason why more and more energetic electrons create these different situations is due to a relation imagined by Luis de Broglie about 100 years ago: the electron, in interacting with the proton, becomes somehow as a wave packet, an ondulatory phenomenon, and the wavelength of this wavy thing is smaller when its energy is higher. So at low energy the electron "wave" sees the proton as a whole: the wavelength is equal or larger than the proton dimensions, and the electron and proton cannot do much more than bouncing off one another. When, conversely, the electron is very energetic, it penetrates inside the garbage bag and hits hard only one of the many things that the bag has inside: a quark or an antiquark. At very high energy we can thus study individual quarks in the proton.
The way we study the contents of the proton, quantitatively, is to measure the deflection angle of the electron and its remaining energy. In elastic scattering, the energy does not decrease significantly, and we get away with just studying the distribution of the scattering angle. In deep inelastic scattering, instead, we need both variables to describe the outcomes. Except that when the energy is really high, we get back to a situation when we do elastic scattering off individual quarks inside the proton: this onset is betrayed by what is called "Bjorken scaling" - a return to a situation when one variable suffices to describe the outcomes.
Through decades of experiments with deep inelastic scattering, the proton has been pictured as the incoherent sum of a number of constituents. Not just the three valence quarks that make up its static properties, but a complex sum of an arbitrary number of parts. In fact, this sum is infinite: if you are willing to consider pieces carrying an arbitrarily small fraction of the proton's own energy, you need an infinite sum.
The energetic electron sees each quark inside the proton through the electric charge that quark possesses - the fact that the two are both electrically charged is what produces the scattering force. But a quark may be found carrying a small or a large share of the total proton energy. Physicsts have devised the concept of "parton distribution functions" to mathematically describe the probability to find in the proton a quark carrying a fraction x (with x from 0 to 1) of the total proton energy (ok, it's actually momentum, but leave me alone, I am simplifying things!).
What was finally obtained was a picture where the proton contains many quarks and antiquarks in addition to the valence ones, and each of these carries a small fraction of the total energy. And the sum of quarks energies is not the total proton energy - about half of it is carried by gluons, the electrically neutral constituents that bind quarks within the proton. Gluons carry the strong force, and without them the electrically charged quarks would quickly move away and destroy the proton. Instead, thanks to the properties of the strong force, protons are perfectly stable and we do not dissolve in a blink into a cloud of quarks.
Parton distribution functions may be a rather obscure concept, but it is easy to show them in a graph (see below). And using their value is also not that difficult: if you want to e.g. compute the probability that by colliding two protons at the LHC you produce a Higgs boson, you "only" have to compute a double integral, where you sum all the combined probabilities that the two partons you collide (one per each of the protons you have thrown at one another) carry fractions x1 and x2 of their protons' energy. To produce the Higgs boson the product of x1 and x2 must be large enough to materialize it from the vacuum: the Higgs boson has a mass of 125 GeV, so you need x1 times x2 to be at least as large as 125/14000, where 14000 is the total energy of the proton-proton collision in GeV.
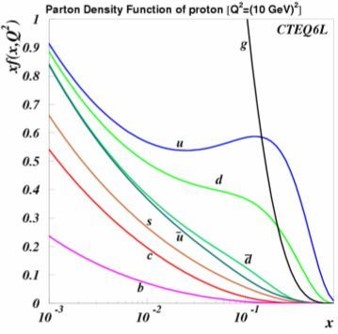
[Above, you can see the form of the proton pdf, pictured for protons that are probed by an electron yielding a squared momentum transfer of 10 GeV^2. Different quarks get different coloured lines, and the y axis represents not the pdf itself but the pdf multiplied by x (the momentum fraction from 0 to 1, which is also the horizontal axis). This is done to allow the plotting of these fractions in a wide range without having them diverging out of the graph for small x values. You can recognize the blue line as the PDF of the up quark (u), of which there are two valence ones producing the hump at x=0.2, and a sea of others that more or less behave as the other curve labeled "u" with an overline. Also note the black gluon, which has a very large probability of being found in the proton - there are many of them, especially at low momentum fraction. Finally, note that a single proton can also, sometimes, contain heavy quarks (c and b), which individually weigh more than the whole proton itself. This is one of the strange things that happen in quantum physics, where Heisenberg's uncertainty principle allows particles to borrow energy from the vacuum, if this happens for a time so short that the vacuum does not manage to file a complaint.]
Of course, the integral you are computing needs to account for the probability that the Higgs boson is materialized given the available energy (larger than 125 GeV), and this requires you to account for the fact that not all partons can do the trick... But at least you now know what parton distribution functions are used for by particle physicists. And you probably have also understood why the proton can really be considered a bag of garbage!



Comments