I believe it may be quite useful if I review here the paper results, and explain to you why they are very important for the physics of the LHC. But first, I feel that there are a few details concerning the process of W+jets production at the LHC which might be obscure to most of you. Let me straighten them out -it is worthwhile to do it!
Preliminaries
At the heart of the matter is a simple fact: W bosons do not possess a color charge as quarks and gluons do, but they are still readily produced in hadron collisions thanks to the electroweak interaction of a quark with an antiquark of different flavour.
If we talk, as we do, about the 7-TeV proton-proton collisions taking place within the LHC circumference, we may picture a red up-quark contained inside a clockwise-moving proton hitting hard a anti-red anti-down-quark contained in a counter-clockwise-moving proton. The electric charge of the up quark is +2/3, that of the anti-down-quark is +1/3, so as the quark-antiquark pair vanishes, the W which emerges gets as a legacy a full unit of electric charge.
Note that above I did not pick the two flavours at random. A up-anti-up pair would not do -the total charge is 2/3-2/3=0, so that pair could annihilate and create a neutral Z boson or a photon, but not a charged W. Even worse would be to pick a up-down pair, which has a fractional total charge (2/3-1/3=1/3): those two guys may jolly well scatter off one another, but they cannot create any new body.
Ok, so we are safe -electric charge is not lost in the sink. But where goes color, the quantum chromo-dynamical charge possessed by quarks ? It annihilates, or more precisely, it does not go anywhere: there is no net color charge in the initial state, since red plus anti-red amounts to zero color, as you can verify in your basement if you have a small-enough mixing bowl.
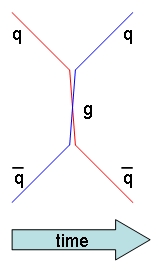Among anti-down quarks, only anti-red ones may produce a W boson by hitting a red up-quark. The other two kinds (anti-blue and anti-green ones, that is) will be capable of interacting with the red up-quark only by exchanging a suitable bi-coloured gluon; again, a sterile scattering process (see diagram, left). Contrarily, in W production the pair of coloured bodies can legitimately vanish and produce a colourless W. The subatomic world is not too different from the macroscopic one: nothing is created, nothing is destroyed, but still in the end everything rots.Seriously, however, let us take stock. First, I draw your attention to the fact that since there are three colours, the requirement that the total colour charge of a annihilating quark-antiquark pair be null makes W production less frequent that it could be; and yet, it is not this colour selection rule what drives the rarity of W production. The process is rare mostly because of the unsurprising fact that weak interactions are weaker than strong ones. The parameters which quantify this difference are the strong and weak coupling "constants": these act as multiplicative factors in the calculation of the probability of emission of the corresponding strong (gluons) and weak (W) vector bosons.
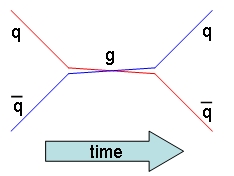The other point to drive home is that quarks, carrying colour, electric, and weak charge (let us waive a discussion on the latter), are projectiles that possess a wealth of different ways to interact. Above I mentioned W production but also Z and photon production (for exact particle-antiparticle pairs), as well as the corresponding scattering processes (where the boson is just exchanged between the colliding pair). A different process occurs if a quark-antiquark pair (say, up-antiup) carries a non-null colour charge: the duo can still annihilate, but the result will be a coloured object - again, a gluon, as shown in the cartoon on the right. The process is the same one seen before, but with time and space coordinates inverted -a unsurprising feature of working in a four-dimensional world where time is just another coordinate.One More Digression: W's Will Not Be Created Equal
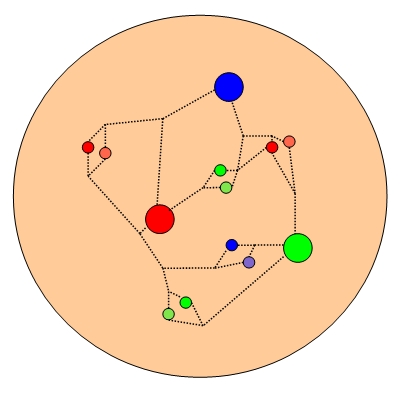Well, it looks like I will really try to take advantage of your patience today. I now draw your attention to another detail: the bodies colliding within the LHC (protons from the East and protons from the West) can be pictured as a bound state of three "valence" quarks (two up-quarks and one down-quark, pictured as large balls in the picture on the right) swimming within a "sea" of gluons and quark-antiquark pairs of all flavours. Forget the gluons (dashed lines) for now -they do not contribute to the most important diagrams of W production; instead, note that in order to yield a W boson, the collision must involve a quark-antiquark interaction; and antiquarks are only found within the proton thanks to its sea of quark-antiquark pairs (the smaller balls in the picture). If the proton did not contain sea quarks, W production would be seriously hindered at the LHC, but still perfectly normal at the Tevatron, where one of the colliding bodies is an antiproton, made of two anti-up quarks and an anti-down one.What happens in most LHC W production processes, therefore, is that at least one of the two protons supplies a sea antiquark. Through a variety of experimental methods, physicists have determined in the last three decades that sea quarks and antiquarks typically carry a much smaller fraction of the proton energy than valence ones.
Since W bosons are heavy enough to require a unusually energetic collision to be created, it follows that the most typical collision resulting in a W boson is one between a soft sea antiquark and a energetic valence quark. But if a valence quark is required, this is two-thirds of the times a up-quark, because of the proton composition. This implies that positive W bosons, created by a up-antidown interaction, are 50% more frequent than negative W ones, which are created by a down-antiup interaction!
Things are not so clear-cut, of course, and as often happens with subatomic reactions, small corrections to a general picture may "soften" the zeroth-order-approximation: yet in the case of the charge asymmetry of W bosons at LHC, the significant difference between the energy fraction of valence and sea quarks keeps the ratio around our eyeballed 1.5.
QCD: Always More Complication Than We Can Use
The inner composition of the proton is tricky enough, but there is much more QCD than that at hadron colliders. Even the "clean" process of W production is messed up by the unavoidable presence of additional quark and gluon interactions, which are obviously governed by strong interactions. Note that when we discuss proton constituents, it is useful to sometimes use the collective word "parton" to label indifferently a quark or a gluon: I will use the term below for simplicity in some cases.
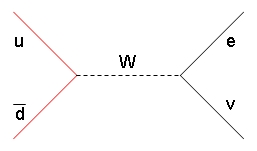At what we call "leading order", W production occurs by the simple reaction already discussed, as depicted in the graph on the right: the two energetic quarks meet at a point, annihilate, the W boson emerges carrying away the energy, momentum, and the combined charges of the colliding pair, and subsequently it decays (very soon -the W has a mean lifetime of about a millionth of a billionth of a billionth of a second!). Such an elegant picture is actually never realized in practice: what happens, rather, is that the colliding quarks before meeting at the point of W creation emit QCD radiation, in the form of gluons. These gluons, in turn, may produce additional radiation. And any of the partons remaining in the final state of the interaction can themselves produce further QCD radiation.
The process of QCD radiation should be understood as a continuum cascading of energetic partons into a larger number of less energetic ones. And there is a problem with calculating the rate of such processes at the blackboard: the number of diagrams to consider grows exponentially with the number of "final state legs" in the diagrams, and the global contribution cannot be evaluated with ordinary "perturbative" methods that work for electromagnetism, due to the large value of the emission probability: adding an infinite series of numbers each much smaller than the previous one is feasible, but adding an infinite series of numbers not decreasing rapidly brings in unsolvable complexities. Fortunately, however, we do not need to wrestle too much with infinite series: experimentally we cannot detect the finest print of colour radiation; we can only detect partons indirectly, if they carry a large energy which they yield to stable particles.
What theorists do when they calculate the rate of these multiple emissions of QCD radiation is to divide the processes according to the number of energetic final state partons that may be created. This allows for a simpler comparison with experimental results, because experiments "see" QCD radiation in the form of individual energetic jets of particles. Each jet is the final product of the fragmentation of a parton emitted in the collision, after the latter has cascaded into a stream of colourless bodies.
Experimenters analyze W boson production events by counting their jets above a specific energy threshold; then they catalog events based on the number and energy of jets that they contain. So if a theorist is to verify whether his theory -Quantum Chromodynamics- agrees with the observed data, she must try to compute the expected rate of W production as a function of the number and energy of the partons emitted together with the W boson.
The job of the theorist is thus to calculate all possible combinations of graphs that lead to the same final state. Let us take W + 4 jets production, the one discussed in the paper: this is produced by processes presenting up to four energetic partons well-separated angularly. Computing all possible combinations of quark and gluon emissions contributing to such a final state is a big headache!
Why W Plus Four Jets ?
But it is important. The W + 4 jet process constitutes the most troublesome and irreducible background to a number of important signals that the LHC experiments want to extract from their data.
I already mentioned a few days ago that in order to discover the top quark the Tevatron experiments had to reduce as much as possible the contamination of precisely those events in their data samples. Back then, in the mid nineties, the theoretical calculations of the process were done at "leading order" (LO), that is by considering only diagrams containing exactly one weak vertex (the one yielding the W) and four strong vertices (yielding a outgoing quark or gluon leg each). The result had a large uncertainty, strongly hindering its usage for absolute rate estimates: because of that, the first top quark searches preferentially made use of data-driven methods to estimate the W+jets background.
Nowadays the precise knowledge of W + multijet production (with a leptonic W decay into electron-neutrino or muon-neutrino) is still quite welcome but it is not as crucial for top-quark physics measurements as it used to be. Still, that process a crucial background to many new-physics searches that the Large Hadron Collider will perform in the forthcoming years. The reason for that is that such a process is the most frequent one among known proton-proton collisions ending up with a final state featuring both a charged lepton, jets, and missing transverse energy; and these components are usually present in the most appealing signatures of new physics.
One example ? Many signatures of Supersymmetry -a theory hypothesizing that for each known Standard Model particle there exists a corresponding super-particle endowed of similar properties but different value of spin- involve jets and leptons, produced during the cascade of squarks (the superpartners of quarks) and gluinos (the superpartners of gluons). The end chain of these cascades is usually a light neutralino, a weakly-interacting neutral particle which may not decay into anything lighter and which therefore escapes undetected, leaving behind the same missing-energy signature present in leptonic W boson decays. Top pair production and W+multijet production are known to be the backgrounds to beat in such searches.
If you are curious about supersymmetric signatures that may be unearthed by the LHC experiments, please see a three-post work on dark matter searches at colliders (part 1, part 2, part 3). Part 3 is the most relevant one, but the preceding others are needed for a clearer picture.
Another example of a hot topic which will benefit from the better-known W+multijet production is the search for fourth-generation quarks. I have discussed that signature and the relative Tevatron searches in great detail in the past, so I will just refer you to a couple of former posts (this one and that one, and why not, also this one) in this case.
The Calculation And The Results
Now let me finally illustrate the results of the new calculation of W + 4 jets production published in the paper cited above. The authors consider a final state of relevance for LHC searches, by selecting processes that yield a charged lepton from W decay with transverse energy above 20 GeV produced centrally in the detector (where both the ATLAS and CMS experiments will detect it with high efficiency). A missing transverse energy above 20 GeV is also required, to match the criterion of a possible loose experimental selection of leptonic W decay candidates; the combined "transverse mass" of lepton and neutrino (identified with the missing transverse energy it produces in the detector) must also exceed 20 GeV.
Finally, jets are considered if they have transverse energy in excess of 25 GeV and a not-too-forward emission angle. These jets are the result of allowing the hard partons calculated with Feynman diagrams to fragment into streams of particles (mostly hadrons, i.e. particles made of quarks), and then operating a jet identification similar to what the experiments do with their observed calorimetric signals.
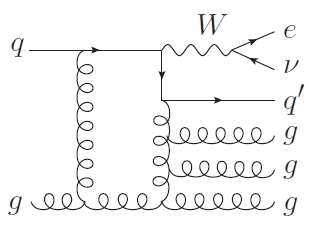The calculation is performed at "next-to-leading order" (NLO) in the strong coupling constant. This means that it includes an evaluation of diagrams containing one loop of partons, such as those shown on the right. The complexity of calculating these diagrams is considerable.A nice outcome of the study is that the inclusion of loop processes reduces strongly the dependence of the result on a unphysical parameter called "renormalization scale", which is needed in all partial calculations. The right value to choose for this scale, which can be thought of as the typical energy at which the interaction takes place, can only be guessed. So theorists need to study our their final results depend on the choice they make of that obscure parameter: that study results in a "uncertainty band" for the measured cross section. That NLO calculations would show a smaller dependence on the renormalization scale than LO ones was indeed part of the motivation of the whole enterprise; but it is surprising to learn that the scale dependence turns out to be reduced almost tenfold, from a 40-60% to a 2-8%!
Authors compare their estimates of the new next-to-leading-order cross section with the old leading-order ones in a couple of tidy summary tables. This means comparing the rate of W production with jets which can be obtained by only considering the simplest, most important Feynman diagrams (LO) with the result which includes diagrams containing parton loops (NLO). The comparison is also made graphically as a function of the jets transverse momentum, evidencing some interesting features: the cross section has a steeper fall with jet momentum at NLO than the old LO result. Good news for searches of new physics, which concentrate at high momenta: backgrounds will be smaller than originally thought!
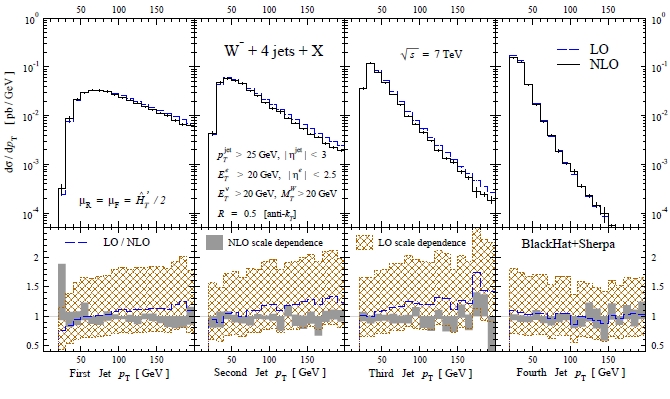
In the top panels of the figure above you can see, left to right, the differential cross section for W production as a function of the transverse momentum of the hardest to the softest jet, for NLO calculation (black) and LO calculation (blue). The bottom panels show the LO/NLO ratios, which evidence a growth with transverse momenta. Note how the large the uncertainty on the LO result (red hatched band) has been reduced to a much smaller band at NLO (the grey one). These results are extremely precise for QCD standards!
Finally, the result mentioned above that LHC collisions should create about 50% more positive W bosons than negative ones is presented in the paper as a function of the number of jets in the final state. I will not paste here the full table, but the prediction is pleasantly reproduced: we go from a 65.6% excess for W + 0 jet production, to a 50.7% for W + 1 jet, to 59.6% for W + 2 jets, 69.4% for W + 3 jets, and 81.7% for W + 4 jets. These are precisely determined numbers, and they constitute a great testing ground for our experiments! The fact that we are discussing ratios of processes makes experimental uncertainties smaller than for absolute rate determinations. I expect that ATLAS and CMS will soon start comparing these NLO predictions with their data.
Comments