It is simple to convince oneself that in order to understand the structure of microscopic objects such as atomic nuclei, ones whose dimensions are way smaller than the wavelength of ordinary light, we cannot just observe them with optical microscopes. Rather, we need to bombard them with something very small, and observe how the projectiles get deflected: as Lord Rutherford first taught us a hundred years ago as he discovered that the electric charge of atoms was concentrated in a small hard nucleus, large deflection angles can only mean that the target atoms are made by hard constituents rather than a undifferentiated blob of goo.
The projectiles of choice for the studies first undertaken by Robert Hofstadter in the early fifties, and later by larger endeavours such as the Stanford new Linear Collider in the sixties, were of course energetic electrons. Electrons are a fortunate choice: they are truly pointlike objects (or at least so they look to us), so the image they deliver of atomic nuclei is sharp. The technology to produce energetic electron beams started to be available in the fifties, and as soon as it was used, it produced dividends.
What one does is to impinge a beam of electrons on a target made of the atoms under study, and observe the rate of scattering as a function of the angle and energy with which the electrons are diffused.
 Theoretically, quantum electrodynamics allows us to compute precisely the scattering rate of pointlike, electrically charged, spin-one-half projectiles from pointlike objects of similar characteristics. (Spin is a quantum-mechanical properties of elementary particles: it can have values in multiples of half the reduced Planck constant, or zero; you can think of it as a measure of the rotation of the particle along an imaginary "axis", although the picture is of limited value, given that a rotation axis has no meaning for a pointlike object, and to other subtler shortcomings.)
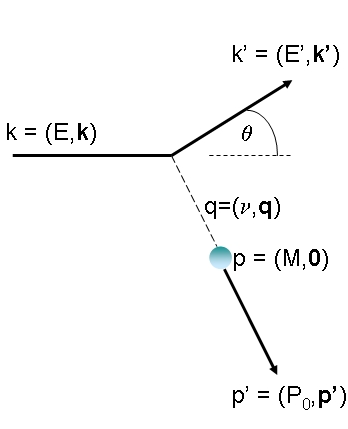
Theoretically, quantum electrodynamics allows us to compute precisely the scattering rate of pointlike, electrically charged, spin-one-half projectiles from pointlike objects of similar characteristics. (Spin is a quantum-mechanical properties of elementary particles: it can have values in multiples of half the reduced Planck constant, or zero; you can think of it as a measure of the rotation of the particle along an imaginary "axis", although the picture is of limited value, given that a rotation axis has no meaning for a pointlike object, and to other subtler shortcomings.)A simplified but effective description involves hypothesizing that the interaction takes place via the emission of a single virtual photon from the electron. The electron scatters as it emits the photon; the photon then "hits" the other electric charge, with a momentum transfer q that depends on the electron energy and the scattering angle theta. The picture on the right above should clarify what I mean. The four-momenta of incident electron (E,k), scattered electron (E', k'), virtual photon (v,q), and target before (M,0) and after (P0',p') the interactions are labeled in the graph as they are measured in the laboratory frame.
It took me about two hours of lesson, plus the grinding on black slate of a half dozen chalks, to go from the enforcing of local gauge invariance of the Lagrangian function of charged fermions (particles of half-integer spin) to the final expression of the scattering cross section of those fermions off stationary pointlike fermions, so I know what I am talking about! It is a tedious calculation involving quite a bit of matrix algebra and several integrals, but I decided to show it in detail to my students despite my course has an experimental cut, because I think any physicist should do the exercise at least once in their life.
The formula one arrives at is called "Mott cross section" and is the following one (gosh, a formula! Surely you have better things to do than stare at a unintelligible string of math symbols ? If that's the case, thanks for the visit. Otherwise, stay focused and you'll grasp the essence of it):
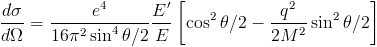
The left-hand side should be read as "differential cross section dSigma per solid angle element dOmega". It is a number which multiplied by an incoming flux allows you to figure out how frequently your electron detector should tick if you place it at an angle theta off the direction of the incoming electron beam. On the right-hand side you have a common factor multiplying two terms within the parenthesis. The common factor is computed from the electron and the target fermion charges (e), some greek-pi factors, and the scattered electron energy E'. Inside the bracket we find two terms: one proportional to the square of the cosine of half the scattering angle, and the other proportional to the square of the sine of half the scattering angle.
What it all means is that quantum electrodynamics predicts that the electron will scatter at an angle theta thanks to the superposition of two forces: a static electric field providing the cos^2 theta/2 behaviour, and a magnetic field produced by the proton spin, contributing a sin^2 theta/2 factor. Note that due to the multiplicative factor on the left of the latter term, magnetic effects only have a role when the square of the four-momentum transfer Q is large: when the electron just passes by at low energy the second term effectively vanishes, as it should since the electron then only feels the effect of a static charge.
The calculation provides a precise prediction for the behaviour of electrons scattered by a pointlike fermion. But that is not what a nucleus is. Hofstadter did extensive studies with atoms of carbon, helium, deuterium and hydrogen, as well as other elements. The simplest are hydrogen atoms, whose nuclei are just single protons. These provide scattering phenomena which are easiest to interpret.
The proton is a charged fermion, and it is a darn small object. So one might try and approximate it as a pointlike fermion, as long as it is not illuminated with the most powerful beams. Experimentally, it was found that at small electron energies the scattered electrons had a distribution similar to that predicted for the elastic scattering formula; however, the structure of the proton already did matter. The proton was seen to behave like a diffuse region of electric charge density and magnetic moment.
Not knowing how to describe the inner structure of the proton, one must insert arbitrary mathematical functions, whose form and value are unknown, in the previously perfectly well determined expressions for the scattering rate of the electrons off pointlike fermions. Then one measures the rate as a function of scattering angle at different values of the electron energy: the data may discriminate good and bad hypothetical functional forms for these unknown functions.
The most general formula which allows the proton electric and magnetic structure to have their say on the electron scattering behaviour is the following one, which now include the
 and
and  "form factors", as they were called back then. As you can easily see, the modification from elastic scattering is not that big!
"form factors", as they were called back then. As you can easily see, the modification from elastic scattering is not that big!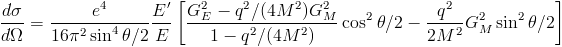
Experimenters found a simple dependence on q^2 of the electric and magnetic form factors of the proton and the neutron (free neutrons as a target are unfeasible, but one can derive their contribution by studying separately hydrogen and deuterium: a single neutron changes the former in the latter).
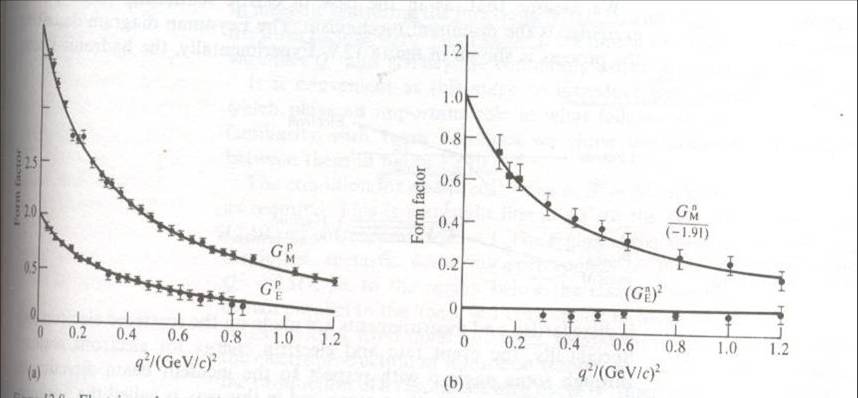
In the picture above, on the left, experimental data show the form factors (extracted from the scattering rate) as a function of the square of the momentum transfer, q^2. The factors behave according to a simple "dipole formula", which implies that the proton looks like a rather simple object, with a distribution of charge and magnetic moment following an exponential distribution. Note that the dependence on momentum transfer of the form factors implies that the electron is seeing an object with an extended structure, with a well-defined characteristic size.
So the data conforms to a simple model, but this does not yet explain much of what the proton and the neutron actually contain. In order to gather more information, higher-energy interactions are required.
 Higher electron energies, up to 20 GeV, were provided in the sixties by the Stanford linear accelerator (see the target area with the big spectrometer on curved rails, left). As the momentum transfer yielded by the electron is brought up to about a GeV and above, the virtual photon behaves like a very short-wavelength probe, capable of penetrating deep in the core of the proton. In this energy regime both the experimental situation and its theoretical description apparently become significantly messier.
Higher electron energies, up to 20 GeV, were provided in the sixties by the Stanford linear accelerator (see the target area with the big spectrometer on curved rails, left). As the momentum transfer yielded by the electron is brought up to about a GeV and above, the virtual photon behaves like a very short-wavelength probe, capable of penetrating deep in the core of the proton. In this energy regime both the experimental situation and its theoretical description apparently become significantly messier. Experimentally, one observes that the proton breaks up, posing the dilemma of whether one should try to describe how the breaking takes place, or just ignore it and insist in studying just the electron deflection and its final energy. Theoretically, on the other hand, one must assume that the previously "simple" electric and magnetic structure functions depend not any longer just on one kinematic variable, but two, reflecting the added degree of freedom.
But it is right then, when one is starting to lose faith in the theoretical description, that a miracle happens. These complicated and a priori unknown structure functions are experimentally seen to behave as simpler functions (let us call them F1(x) and F2(x)) of just one dimensionless ratio x, constructed with the energy and momentum transferred from electron to proton and the proton mass.
The onset of a behavior whereby the probed proton structure ceases to depend on dimensionful parameter (the scale of the proton itself) reveals what is actually happening: at these higher incident energies we are effectively illuminating the individual components of the proton, which are pointlike for all practical purposes, and thus cannot be described by a length scale.
With deep inelastic scattering of electrons off protons we have thus taken the first pictures of the quarks! These are not pictures in the sense we are accustomed to in our daily life, and yet they have the same meaning: the pattern of electron diffusion off protons shows indirectly their image.
And there is more: if an elastic scattering is happening between electrons and individual quarks, we can test whether the latter have the same spin properties of the proton. Protons and electrons are fermions, as they carry a half unit of spin. The spin of the proton causes the electron to scatter elastically from the combination of an electric field and with a magnetic one. If quarks have zero spin, the rate of electron scattering at a given angle is different from what it is if quarks have half unit of spin.
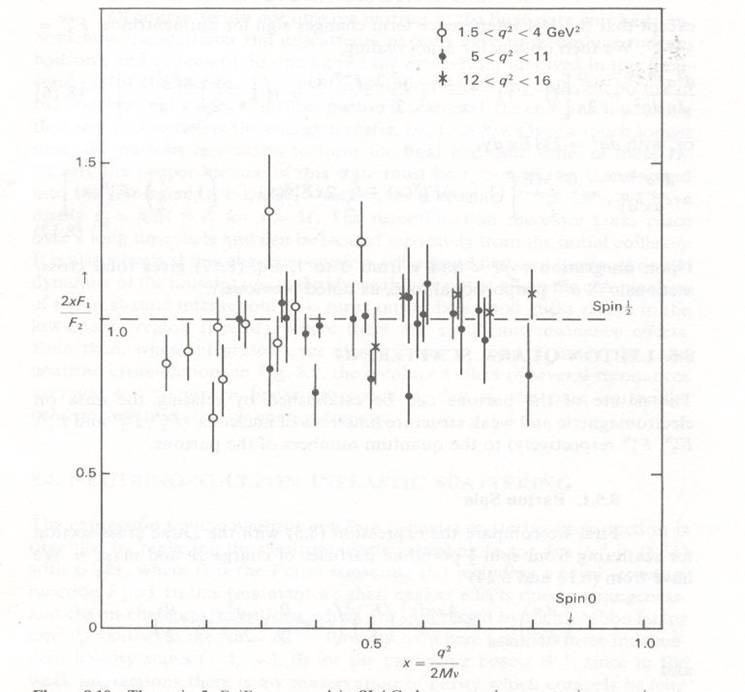
The figure above shows that indeed, in inelastic electron-proton scattering quarks are seen to behave as pointlike, charged, spin-1/2 particles. If they had zero spin, the experimental points would line up at zero. The equality to one of the ratio between the two structure functions F1 and F2 (
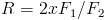 , where x is the fraction of momentum of the struck quark) is called Callan-Gross relation.
, where x is the fraction of momentum of the struck quark) is called Callan-Gross relation.The relevance of the studies of "deep inelastic scattering" of electrons off protons cannot be overstated: while the experiments I described above were performed half a century ago, they retain a high value today. In fact, the structure functions of the quarks in the proton are measured with high precision nowadays, but their indetermination still remains one of the leading sources of uncertainty in the rate of standard model processes we produce at the Large Hadron Collider when we smash protons against other protons at a centre-of-mass energy of 7 TeV: any measurement we do requires a detailed study of these systematic uncertainties!





Comments