Quantum physics has proven that the world cannot be described by local realism. Therefore, Many-Worlds Interpretations (MWI) are now in vogue.
 This is already wrong: Everett's is a relative state description, not necessarily a multiple worlds interpretation.
This is already wrong: Everett's is a relative state description, not necessarily a multiple worlds interpretation.
Below is my “cut a Wiener sausage from both ends” model that illustrates the concept as applied to the famous Einstein-Podolsky-Rosen paradox. A correct quantum version of this model is possible. The MWI in its modal realistic many-minds versions [see also Nonlocality versus Antirealism] is the mature way to understand modern physics.
UPDATE:What is written in this post is now mostly much better accessed in this, extremely pedagogically written article [3]: http://arxiv.org/abs/1311.5419
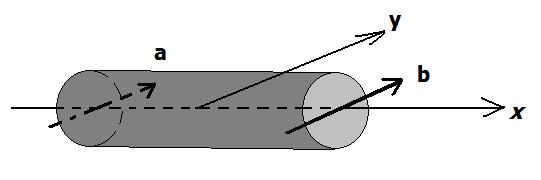
Alice and Bob each chose a measurement direction, a and b respectively, and each measure one photon of an entangled pair of photons. Alice is on the left and Bob on the right. The two entangled photons travel from the middle to the left and right, respectively, along the x-direction. All is as I described in detail before in the well known and simple setup. Say Alice and Bob both measure along the y-direction, that means a and b are parallel and both point along the y-direction toward the back:
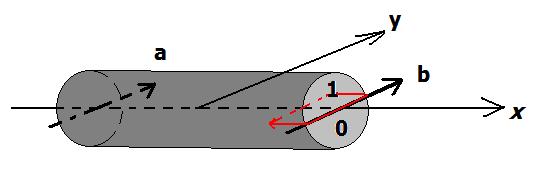
Imagine that when Bob’s photon arrives at Bob’s place (right end of Wiener), the world starts splitting there according to a right hand rule: The arriving photon’s propagation direction (positive x-direction) goes along your right thump and b along the index finger, hence the usually longest “flip-the-bird” finger now points upward. That is where the worlds are that have Bob measuring the polarization B = 1. In the lower half of the sausage are all those worlds that measure B = 0.
The split (red) is the "dislocation of decoherence" that travels with light velocity towards the left to Alice, splitting the world like a zipper, to use H. Dieter Zeh’s words [1]. Basically, Bob’s measurement cuts the Wiener with a knife held horizontally, splitting it into two parallel worlds.
The same happens on the left when Alice measures, only that Alice’s photon propagated along the negative of the x-direction, so the same right hand rule results in the worlds with A = 1 to be towards the bottom:
Alice and Bob cut the quantum universe along the same plane! The result is that there are only two kinds of worlds once the split is complete, namely those where (A,B) is equal to (0,1) and those where it equals (1,0). Both halves' volumes are 50% of the total and thus equal to the correct quantum probabilities.
Now we look at what happens if Alice has her measurement angle at 45 degrees instead.
UPDATE: The following using a doubling of angles may have confused readers. A perhaps better version is now posted.
Note that I do not have a z-axis yet in this model. The y-axis in the model corresponds to the real y-axis, but the z-axis in the pictures is NOT the real z-axis. This is because the model must take care of the so called “double covering” that electrons for example are susceptive to – I will not go into this here; it is the usual SU(2) group issue about having to turn around twice to get back to the original state. Suffice to say, the actual angle between the y-axis and the direction a leads to double that angle in my sausage model picture; φ = 45 degrees are here 2φ = 90degrees:
For Bob, everything is initially the same, but for Alice, the right hand rule will now put the A = 1 worlds to the back and the A = 0 ones to the front of the sausage. Since directions a and b are not parallel anymore, the sausage rips up into four kinds of parallel worlds:
The volume of each kind of world is 25%, consistent with quantum physics.
I am in no mood to draw pictures for other angles. The same game leads to always four different kinds of worlds, namely (0,0), (0,1), (1,0), and (1,1). It is pretty easy to see that their volumes areas follows:
If the whole sausage has volume V = 1, and the relative angle between a and b is δ (in the real world, so it is 2δ in the picture), the volumes V(A,B) of the split-off worlds (A,B) are
V(0,0) = V(1,1) = [2δ/π]/2
V(0,1) = V(1,0) = [1 - 2δ/π]/2
Now you could think that if you just work on this model a little, surely you can find shapes of sausages or whatever other modification in the angles or even photons so that the volume V equals the quantum probabilities P:
P(0,0) = P(1,1) = [sin2(δ)]/2
P(0,1) = P(1,0) = [cos2(δ)]/2 = [1 - sin2(δ)]/2
They are the same at δ = 0 and δ = π/4 = 45 degrees and otherwise similar except for the 2δ/π being instead sin2(δ).
You could now think that this model shows how many worlds can be intuitive, how they explain non-locality without “spooky action at a distance” (nothing faster than light!). You could be seduced to think that there are no hidden variables here and that the splittings cut the world along the measurement directions, which indeed does touch on profound insights. The volumes depend on the relative angle between the cuts, which are only known wherever both cuts, the one from Alice’s measurement and the one from Bob’s, have traveled already. It seems non-local.
However, you would be wrong! What is wrong? I let you ponder about it and give the answer another time. Well, here are some more hints in the new version (and the solution is now posted, too.).
------------------------------
[1] H. Dieter Zeh: “Quantum discreteness is an illusion.” arxiv:0809.2904
[2] S. Vongehr: "Many Worlds Model resolving the Einstein Podolsky Rosen paradox via a Direct Realism to Modal Realism Transition that preserves Einstein Locality" arXiv:1108.1674v1 [quant-ph] (2011)UPDATE: Reference [2] is the first paper on the possibility of such models, but the models have now actually been constructed and are much better explained in:
[3] S. Vongehr: “Against Absolute Actualization: Three "Non-Localities" and Failure of Model-External Randomness made easy with Many-Worlds Models including Stronger Bell-Violation and Correct QM Probability” http://arxiv.org/abs/1311.5419 (2013)










Comments