Many Worlds by Splitting a Wiener Sausage is extremely simple as far as models go. Before we can resolve the Einstein-Podolsky-Rosen paradox with it however, we need to understand what is still wrong with it.

It is “wrong” for a simple reason that I wrote about in several other posts, and anybody who understands the EPR problem to some degree should know the correct answer, regardless of whether they trust Bohm, or “believe Copenhagen”, or subscribe to locality, non-locality, many-worlds, objective state collapse into one world, whatever!

The correct reason can be put into a short sentence. That none was offered, reflects the lack of insight into these widely popular and written/read about issues. Popular science books are apparently only commercial successes, but else fail; university physics/philosophy education does not do well either in terms of getting actual understanding of topics across.

One can resolve the EPR-paradox with the sausage model via a step which obviously modifies realism while letting locality untouched [see also Nonlocality versus Antirealism on why such is expected]. If you desire to go there and understand EPR for the first time, you need to understand the sausage model, and you only understand it, if you can tell us its main shortcoming as far as it is introduced now!

So I will present it again today, this time without the perhaps confusing “double-cover”, but introducing a method to reproduce the factors that are proportional to the quantum probabilities. Here is the “cut a Wiener sausage from both ends” model once more briefly recaptured; if you remember, jump below the second hatched line.

UPDATE: What is written in this post is now mostly much better accessed in this, extremely pedagogically written article [2]:  http://arxiv.org/abs/1311.5419

------------------------------------------

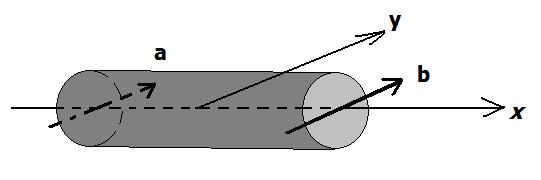
Alice and Bob each chose a measurement direction, a and b respectively. Alice is on the left and Bob on the right. Two entangled photons travel from the middle to the left and right, respectively, along the x-direction. All is as described in detail before in the well known and simple setup. Say Alice and Bob both measure along the same direction, that means a and b are parallel:

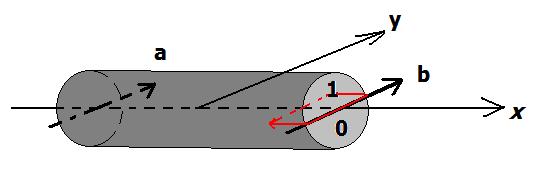
Imagine that when Bob’s photon arrives at Bob’s place (right end), the world starts splitting there according to a right hand rule: The arriving photon’s propagation direction (positive x-direction) goes along your right thump and b along the index finger, hence the usually longest finger now points upward. That is where the worlds are which have Bob measuring the polarization B = 1. In the lower half of the sausage are all those worlds that measure B = 0.

The split (red) is the “dislocation of decoherence” that travels towards the left to Alice, splitting the world like a zipper, to use H. Dieter Zeh’s words [“Quantum discreteness is an illusion.” arxiv:0809.2904]. Basically, Bob’s measurement cuts the Wiener with a knife held horizontally, splitting it into parallel worlds.

The same happens on the left when Alice measures, only that Alice’s photon propagated to the negative of the x-direction, so the same rules result in the worlds with A = 1 to be towards the bottom:

The result is that there are two kinds of worlds once the splitting is complete, namely those where (A,B) is equal to (0,1), and those where it equals (1,0). Both halves’ volumes are 50% of the total and thus equal the worlds’ probabilities.

-------------------------------------------

Let me present arbitrary angles differently today, avoiding the doubling of angles.

We add another cutting wire: If a crystal’s internal y-direction and z-direction both cut, every measurement will split the sausage into four equal pieces. The worlds where the measurement outcome is zero are in opposing quadrants. In Alice’s case for example, A = 0 worlds are in the first (between her crystal’s internal z= a and y directions) and third quadrants (Next figure a). The sausage finally falls into eight pieces (Next figure b): four different kinds of parallel worlds (A,B).

The cross-section of the probability sausage as seen from Bob’s perspective: a) Alice’s measurement splits it into four quadrants. b) Where the world-splitting from Alice’s and Bob’s measurements have both arrived, the world has branched into eight sections but only four types of parallel worlds (A,B).

If the sausage has unit volume and the angle between a and b is δ = beta–alpha, the volumes V(A,B) of the parallel worlds are V(0,0) = V(1,1) = |δ|/π and V(0,1) = V(1,0) = ½ –|δ|/π. This differs from the quantum physical probabilities only by the substitution of |δ|/π for ½ sin²(δ).

Let’s introduce not just four cuts for each measurement, but instead very many cuts and an angle specific density f of cutting wires. The cuts approach each other from both ends like always. Where they meet, the total number of cuts in the V(1,1) parts of the cross-section are proportional* to ½ sin²(δ), which is the correct quantum probability.

You could now think that this model shows how the many worlds concept can be intuitive, how it explains non-locality without Einstein’s “spooky action at a distance”: nothing goes faster than light does! You could think that there are no hidden variables here and that the splits cut the world according to the measurement directions. The volumes and also the number of cuts inside of them depend on the relative angle between the cuts, which are only known wherever both cuts, the one from Alice’s measurement and the one from Bob’s, have traveled already. It seems non-local enough.

However, you would be wrong! What is wrong? (Hint: think in terms of the Quantum Randi Challenge and about realizing the model with help of computers. The solution is now posted here, and the next to final step in solving the EPR problem correctly [1] is here.)

--------------------------------------

* f depends on the angle from the crystal’s z-axis, i.e. f(alpha’) at Alice’s end. The right hand rule implies that alpha’ increases counter clockwise from the a axis; beta’ increases clockwise starting from b. The number density f increases sharply to reach a maximum around Pi/4, after which it tails off.

[1] S. Vongehr: "Many Worlds Model resolving the Einstein Podolsky Rosen paradox via a Direct Realism to Modal Realism Transition that preserves Einstein Locality" arXiv:1108.1674v1 [quant-ph] (2011)

UPDATE: Reference [1] is the first paper on the possibility of such models, but they have now actually been constructed and are much better explained in [2] S. Vongehr: “Against Absolute Actualization: Three "Non-Localities" and Failure of Model-External Randomness made easy with Many-Worlds Models including Stronger Bell-Violation and Correct QM Probability”
http://arxiv.org/abs/1311.5419 (2013)