You may suspect the beating of a dead horse by now, but the problem is actually that the animals in question are still alive. As was discussed, the alive cats expect to see something when the box opens.
If we interact with the Schrödinger cat superposition state inside the otherwise isolated box so that we will only have dead cats result, what do the alive cats see? There must be a place into which those cats can jump. However, it cannot be the room where the experimenter observes them, since the experimenter only observes dead cats after having applied the ‘rotation’.
Judging from the comments, this question is harder than anticipated, so before merely giving the solution, let us clarify the problem further. It is worth it, because the answer is quite simple and not at all philosophically nebulous, though certainly philosophically relevant.
The Mechanism
The dead/alive decision is simply made by a linearly polarized photon with a polarization of about 18.4 degrees to the vertical. Going through a beam splitter that separates vertical (V) and horizontal (H) components, the photon will come out vertically polarized with a probability of about 90%. That is because Cos2(18.4 degrees) = 0.900366. If so, the photon goes through a channel labeled “V=Alive”.
In 10% of all cases, the photon instead emerges horizontally polarized, goes through the “H=Dead” channel, upon which it hits a detector that triggers the subsequent shooting of the cat, which thus also ends up in a horizontal position – no way I could resist this pun ;-).
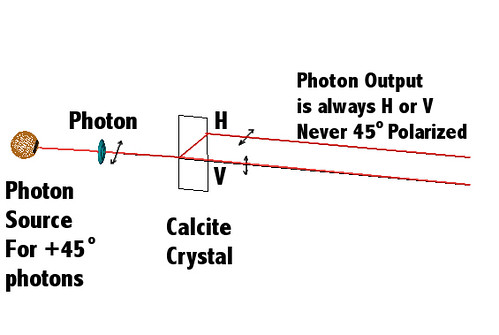At 45degree input polarization, the probability to have the photon come out horizontally polarized is 50% [Cos2(45 degrees) = 0.5].
The Rotation
The rotating I invoked is an effective (see below) rotation of the polarization angle from 18.4 degrees to 90 degrees. It is not just a rotation of so called phases, which indeed would not change probabilities. The proper rotation will lead to the resulting photon reaching the “V=Alive”-channel with zero % probability [Cos2(90 degrees) = 0].
With other input polarizations, the probability can be adjusted from zero to unity.
In order to effectively rotate, I need to effectively resurrect the state of the photon as it was before it split into two different histories, |V> and |H>. To make the splitting effectively undone is relatively easy experimentally, as long as the |V> and |H> states are not entangled with something as complicated as a cat.
“Effective” means the following: I may refuse to practically put the horizontal and vertical polarizations of the photon back together, to practically resurrect the previously 18.4 degrees polarized photon. After all, it split already some time ago! I may act on the (during time evolved and with the cat entangled) |V> and the |H> states both in such a way that the result is the same as if I first resurrected the previous polarization, then rotated that photon, and then split it again into the V and H components. There isn’t any difference, neither relative to the different states nor in the end result. This is reflected also in the fact that one can describe the procedure in the mathematical formalism using any basis, {|V>, |H>} or {|+45>, |-45>}, or any other complete basis. The |V> is always |V>, |Alive> is always |Alive>.
This setup should help you to differentiate the easy part that has been experimentally accomplished already, from the hairy part, the cat. In fact, it may help to consider having the cat and the gun inside a further isolated box inside the box, while initially only the one photon, being in the V/H superposition state after the beam splitter, enters that smaller box. We can always bring everything down to well defined photons being allowed to enter otherwise completely isolated boxes containing in principle well known states. No “philosophizing” necessary.
Now you may bark “‘In principle well known states’ my dear behind!” Well, by “cat” the experimental physicist means any molecular system complex enough to have some sort of memory upon interaction (the cat's observation), so actual experiments should be possible relatively soon (see for example [1] and references therein).
Anyway, here it goes to the solution.
-------------------------------------------
[1] Jae-Seung Lee, A K Khitrin: “Resurrection of Schrödinger's cat.” New J. Phys. 8,144(2006)
