Schrödinger’s cat is in a quantum superposition of two states, namely |Dead> and |Alive>. If we open the box and find the cat dead, where is the living one? You all know the answer: In the ‘parallel universe’ where I pull the cat out alive. Let me add a twist that only a true cat hater can come up with.

In short, I will use quantum interaction to let the probability of observing a dead cat go to 100% without destroying the alive state. I pull only dead cats out and the alive ones have no parallel universes where I take them out of the box, thus they have nowhere to go when the box automatically opens, except for jumping straight into hell. Muahahahaha!!! Well, actually they won’t, but I will ask you to provide the correct answer for where they go: A new didactic challenge! (BTW: Has anybody ever suggested this scenario before? If so, please let me know.)

A mechanism inside of my box will kill everything inside of the box with a 10% probability at the one minute mark. After three minutes, the box automatically opens. Hence, after three minutes, in nine out of ten cases, I could see a healthy cat jumping out of the box. But cats are dirty and stink, as is widely acknowledged in the research literature, so at the two minute point, I do something a little different.

I send photons into the box. The photons are known precisely, so they will not ‘collapse’ the state. What does “not collapse” mean? If it collapses into a classical ‘statistical mixture’, we just do not know the state, whether it is dead or alive, but it is already one or the other. In the non-collapsed quantum case, we may know the state of the cat to be precisely Ψ = [|Dead> + i |Alive>]/2^1/2, for example, so it is strictly not yet decided.

In principle, I can design the photons to be in such a configuration that they will effect any desired interaction with the box and its internal mechanisms, the cat and so on, in such a way, that the superposition state stays to be a true quantum superposition of |Dead> and |Alive>, while however changing the amplitudes of the states. I can make the observation of one of them, say |Dead>, twice as likely to be observed than the other: Ψ’ = [ 2 |Dead> + |Alive>]/3^1/2

The photons I send into the (otherwise totally isolated) box are designed to ‘rotate’ the superposition state in such away that the probability of observing the healthy cat becomes zero. This does not kill the cat in the |Alive> state! Think of a photon in a diagonal polarization state, which is always a superposition of horizontal |H> and vertical |V> polarization. If you rotate the polarization from being diagonal to being a little closer to horizontal, observing the |H> state becomes more likely, but only because the factors in front of the states change inside the superposition. The states themselves are unchanged: |H> and |V> stay the same all the time.

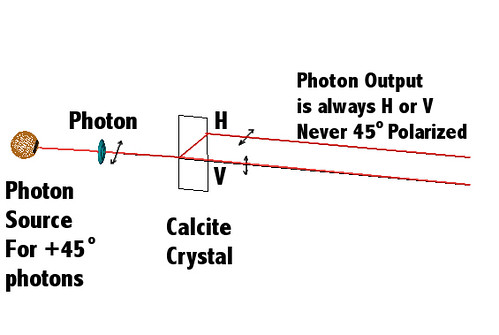
At 45 degree input polarization, the probability to have the photon come out horizontally polarized is 50%.

With other input polarizations, the probability can be adjusted from zero to unity.

I ‘rotate’ the state inside the box, which is a state that I have previously prepared, so I know it and can thus change it at will. Cats are nasty, therefore I ‘rotate’ it so that the probability for finding |Alive> goes down to zero. After three minutes, the box opens and I find a dead cat every time I run the experiment. Where are the healthy cats?

We know that there are healthy ones! The whole point of the Schrödinger cat problem is that we could always interrupt this experiment at the two minute mark, at which point we would find a healthy cat nine times out of ten when opening the box. Those cats are in the box at the two minute point and further, every time.

Imagine you are the cat. You witnessed me already turning ten other cats before you into dead meat. Now it is your turn; I stuff you into the box. Imagine you sit in the box for longer than a minute already; you survived, so far so good. At the two minute mark, I let photons enter the box, but remember, it is done so that you, the cat, do not perceive them. All the photons do is to bring the probability of the |Alive> state being afterward observed by me to zero. But now you start wondering, the third minute comes up and the box opens: What do you, the cat, see?

Erwin:“No Honey, the coin isn’t conscious!”

The experiment makes only sense if all the cats that are retrieved from the box are dead, because only then does it become interesting to imagine the cats’ situation: They expect to survive (with 90% chance) until the three minute mark, at which the box opens, but then there is no parallel universe in that they can step out to! So, what happens to all those cats?

Wrong Answers:

You may think that in a multiple world description, there is a universe where I am a cat lover and therefore manipulate the superposition state to result only in alive cats. However, the reason for making only dead cats is not only that I hate felines (actually, they taste quite delicious). The real reason is: An experiment that allowed for alive cats is not interesting because getting out alive cats just has dead cats disappear.

Dead cats are not conscious anyway, thus there is no mystery in them disappearing. The complimentary experiment is not scientifically interesting, and thus there is no parallel universe where I perform such an experiment.

Certain other answers are also not right: I do not want to hear about gravity and the Penrose Diosi limit – we assume here that linear quantum mechanics works for cats.

The answer is also not a quantum immortality scenario, where in a few parallel universes due to some quantum tunneling some mishaps occurred and the photons did not rotate the superposition properly and so the healthy cat can come out with 100% probability relative to the cat although it is only 0.0000000…1% from the experimenter’s point of view. This does not work here, because the |Alive> cat state that I am asking for is one that even at close to three minutes is entangled with the correct and intended photons while the one that would survive in this “shit always happens” scenario is one that could be shown to be different, i.e. one with some sort of mishap having occurred when preparing the photons.

UPDATE: The solution to the problem is now posted here.