Recently this headline on Real Clear Science caught my eye: Carbon-12 Nucleus Shaped Like Equilateral Triangle.  It led to an article in Physics World, entitled

Carbon nucleus seen spinning in triangular state

This is one of the many sorts of things that fascinate me, and so I started chasing press releases and original papers.  Now Wikipedia tells us that

Stories or narratives have been shared in every culture as a means of entertainment, education, cultural preservation, and instilling moral values.

I feel that the storytelling element is so often left out of science, and here is a story to tell that links the beamlines and the stars, and so, like the chap in the picture, I will begin, but first:

Disclaimer: any howlers in this presentation are property of the author, and not to be attributed to the University of Birmingham.

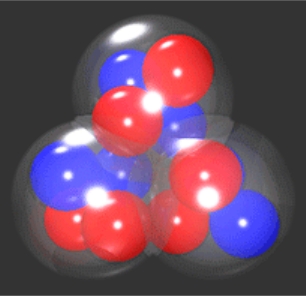
Triangular nuclei!  This sounded like something really new to me.  Since my student days, all I ever came across was the earlier Liquid drop model, which did account for the masses of nuclei, and the rather more sophisticated Nuclear Shell Model, which effectively held the field.  One imagined a ball stuffed with protons (red) and neutrons (black or blue).  But not everybody was satisfied with it, in particular two workers in Mexico and the USA who from 2000 started publishing a new model,

The Algebraic Cluster Model: Three-Body Clusters

So how does one actually ‘look’ at a nucleus?  The customary procedure is to fire particles at it, for example electrons.  As the paper above states:

Form factors for electron scattering on ¹²C were measured long ago.

From which one gets a scattering pattern to which one can apply a battery of mathematical methods.  However, one can often take two or more different models and fit them all to the experimental data within the range of uncertainly – particularly statistical uncertainty – arising from the data.  Often, what one wants is a more sophisticated method of data collection.  Enter the University of Birmingham and their cyclotron. 

How many of our readers outside the UK have heard of the expression a “Birmingham Screwdriver”?  This means a hammer, and is a joke at the expense of the people of Birmingham, implying that they are inclined to the use of brute force and ignorance.  (Though I have not found this with scientists either at or from Birmingham.) With the Birmingham cyclotron, the team bombarded the carbon nuclei, not with light electrons, but much more massive and energetic alpha particles (strictly speaking, a product of radioactive decay, but now generally used interchangeably for a helium nucleus without its electrons.)

It may sound like using a sledgehammer to crack a nut, but what is achieved here is to knock the carbon nuclei from their ground state into higher states.  A carbon nucleus is a pretty stable thing, likely to last for years on end, possibly until disrupted by proton decay, a very slow hypothetical process and one which has not yet been observed.  But there haven’t always been carbon nuclei around.  There were none present immediately after the Big Bang, and they only appeared after being cooked up in giant stars by the collision of three alpha particles.  But that creates a carbon nucleus in an excited state, and it quickly has to dump its energy somewhere or it will fly apart again into three alpha particles.  But if it manages to dump that energy it will now sit happily, since it will not have enough energy to break up again.

Now when carbon nuclei in the target – at Birmingham a thin film of carbon about half a micron thick – are hit by alpha particles, they go into an excited state which has enough energy (or is sufficiently energetic, to use more formal language) to fly apart.  This creates a shower of four alpha particles: the one from the beam which hit the target, and three from the nucleus.  But the three don’t all appear immediately.  The nucleus breaks first into a beryllium-8 nucleus and an alpha particle, and in less than 10^-16 seconds, most of the beryllium will have split up again into two alpha particles.  (This extremely short half-life is why higher nuclei could not be created at the Big Bang: ⁸Be nuclei simply would not hang around long enough to capture any more neutrons.)  One cannot observe the ⁸Be nuclei directly: they’re like those extremely short-lived massive particles created in the Large Hadron Collider: not observed directly but inferred from the showers of particles created from their decay.

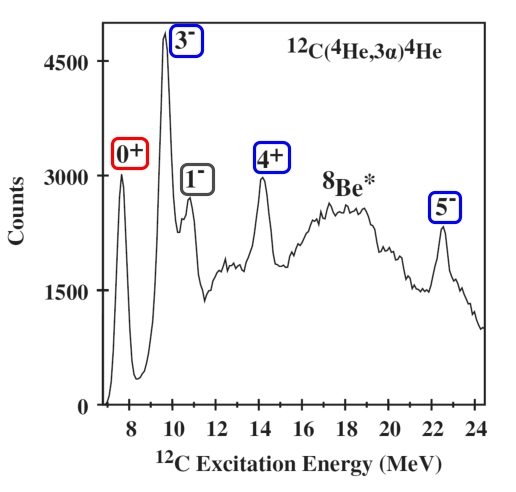
In these experiments, it was not possible to collect all four alphas from any one shower, only three.  However, it was possible to discern whether those three contain the pair that resulted from the decay of the transient beryllium, and select only those for analysis.  From that one can calculate the energy of the carbon nucleus as it broke up, namely the rotational and vibrational energy, minus the energy that was lost as the particles flew apart.  Here, after all the processing, is a graph of counts versus energy of state from which they came.  On the left hand side, it stops at an energy of just over 7 MeV, because below that, the nuclei simply won’t break up.  Note that everything here refers to an alpha-particle: the ⁸Be* refers to alphas derived from beryllium nuclei in states of greater excitation.

And next, here is a graph of what one derives from this.

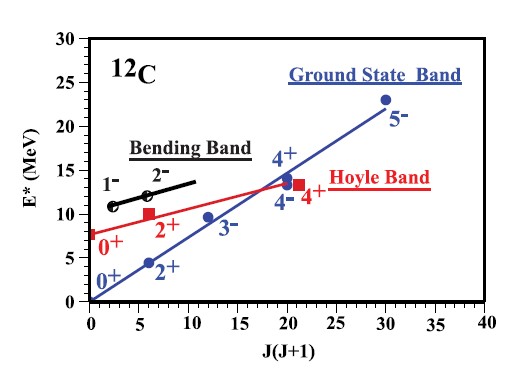
The left-hand axis shows the energy of the observed or calculated state, with 0 representing the energy of the nucleus as ordinarily found.  Alpha-impact can make these nuclei rotate, and the blue diagonal line refers to different rotational levels derived from the ground state.  In the classical world, one can pluck a guitar string to (within reason) any amplitude one wants, but down at the quantum level – a vibrating molecule for example – energy comes in packets.  For a diatomic molecule such as oxygen for example these packets are effectively equal, so vibrational energy levels are spaced uniformly.  With rotation, though, it takes an increasingly bigger step to move up from one rotation state to the next faster one, so that the rotational energy follows a series proportional to 2, 6, 12, 20, 30 which are 1×2, 2×3, 3×4, 4×5, 5×6, etc.  That is where the J(J+1) comes from along the bottom axis.  (This behaviour is both observed experimentally and predicted from solutions to the Schrödinger wave equation.)

In the experiment, the blue 0+ and 2+ states are not observed, since the nucleus is not energetic enough to fly apart.  The 3– and 4+ however, are observed, and new to this experiment, the 5– for the very first time.  By fitting the calculation so well, this extra point is even more evidence that the carbon-12 nucleus is made up of a triangle of alpha particles.

There is also the black 1– state.  Not very energetic as far as rotation goes, but this fits a calculation where the nucleus is vibrating so that the equilateral triangle is bent out of shape.  The energy of this vibration is quite significant, enough to take the nucleus over the break-up threshold.

So far, we’ve been quite down-to-earth about all this.  But there is at least one other state observed, and one that takes us to the stars.  This is the Hoyle state, predicted in the 1950s as being necessary to account for two things.  First of these was the existence of elements heavier than helium in the universe.  Fred Hoyle was the chief proponent of the Steady State Theory, according to which hydrogen atoms were continuously created to keep the density of matter constant as the universe expanded.  Fusion to helium was already (mainly) accounted for by the proton-proton chain as put forward by Hans Bethe in 1939.  The Big Bang Theory gives one hydrogen and helium, but again, no carbon or higher.

Hoyle predicted that there must be such a state of the carbon nucleus.  Stars such as Arcturus get most of their energy from helium burning, but two alpha-particles could only to combine to form beryllium-8 which one would expect simply to fly apart, and all that energy would be lost as soon as it was generated.  But if, during its very short lifetime, it collided with another alpha-particle, it could form carbon-12.  However, this would not be ground-state carbon as in a lump of charcoal — it would need to be an excited state.  In the near vacuum of the cyclotron, this would again fly apart, but squashed together with lots of helium nuclei in the middle of a star, it could quickly dump that excess energy onto some of them.  Nice in theory, and to make it into practice, the state was observed at Caltech in 1953, effectively proving the theory.  This made it into the mainstream with the publication of the most classic B²FH paper in 1957.  It is, however, something of an irony that the work of Hoyle, the chief Steady-Stater, turns out to be a necessary accompaniment to today’s Big Bang Theory.

But the Hoyle state is no longer confined to stars.  In the two graphs, indicated by red, is the 0+ (lowest rotation) mode of the Hoyle state, now observed at Birmingham.  The two higher ‘red’ states in the bottom graph are calculations, made assuming that the Hoyle state is also triangular, but vibrating so as to expand it into a triangle larger than the ground state.  There may be hints of them in the plot of counts, but not clear enough to say categorically that that is what they are.  To obtain such precision, one would need to employ gamma-ray bombardment, and one assumes research grant proposals are in the pipeline, but how far along is not stated.  Then one could be more certain that the Hoyle state is also triangular, rather than the “bent elbow” that other models have suggested.  Indeed, as this short article from Birmingham Life, Bent Chains, and the Anthropic Principle (well worth reading) suggests, only four years ago the “bent elbow” was still largely unchallenged.

Red giant stars do not stop at carbon, but go on to convert this into oxygen (and even higher elements, if the star is massive enough.)  But as they come to the end of their fusion lifetime, much of the carbon and oxygen will be puffed into space, to end up in stars formed later.  Our own Sun contains C and O from earlier stars.  But if there is not enough hydrogen left to form new stars, one can end up like this: Red And Dead - The Carbon Monoxide Future Of Galaxy ALESS65.

All of which got me thinking: if the carbon-12 nucleus is made up of a triangle of alpha-particles, could the oxygen-16 nucleus be made up of a tetrahedron of them?  I am not the first to think of this.  Here is some news from North Carolina (nothing could be finer):

Researchers Describe Oxygen’s Different Shapes which refers to a paper Ab Initio Calculation of the Spectrum and Structure of ¹⁶O where calculation shows that the ground state should indeed be tetrahedral.  However:

[they] found their lattice revealed that although both the ground and first excited states of oxygen-16 “look” the same in terms of spin and parity, they are in fact quite different structurally. In the ground state, the protons and neutrons are arranged in a tetrahedral configuration of four alpha clusters containing two protons and two neutrons each. For the first excited state, the alpha clusters are arranged in a square.

I hope you all have enjoyed our little excursion to the wonders of the atomic nucleus.  But if you would like a little musical entertainment to finish, take a look at this picture of the evolution of a star with mass like our Sun (adapted from this Wikimedia Image) :

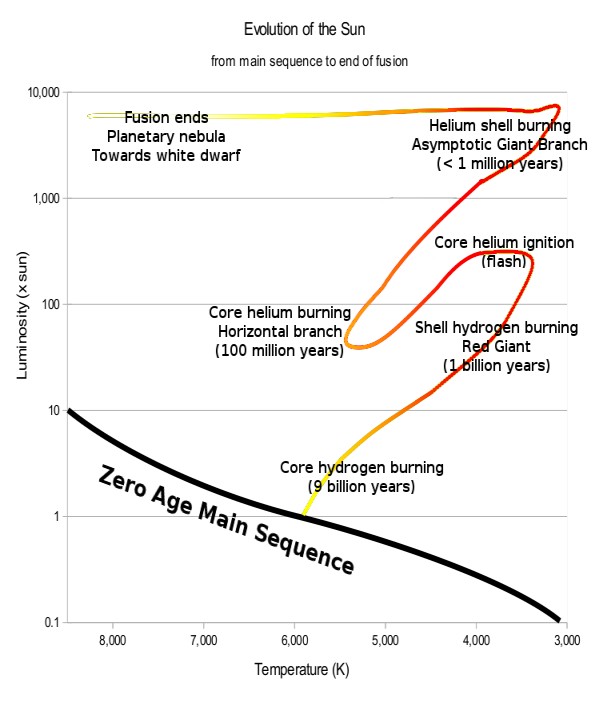
It shows two stages of expansion, first as a “ordinary” red giant during the phase of shell hydrogen burning, then as a much bigger red giant during shell helium burning.  In Rossini’s overture “The Thieving Magpie”, there are two characteristic Rossini crescendos, one starting at 5:30, and a reprise of the same at 8:40 in the YouTube below.

Somehow, I made the connection between these  two crescendos and the expansion phases of the star, round about the year 2000, and it sticks with me.